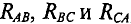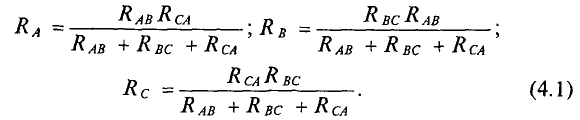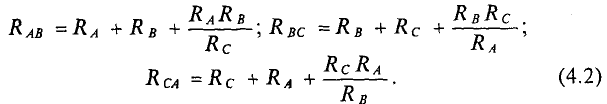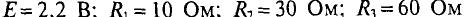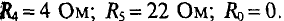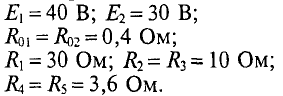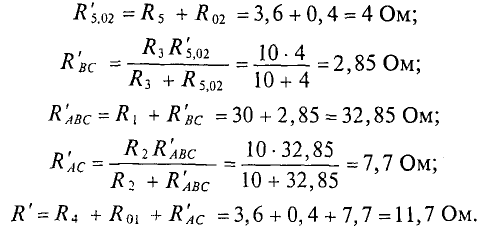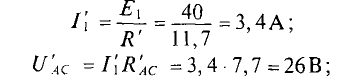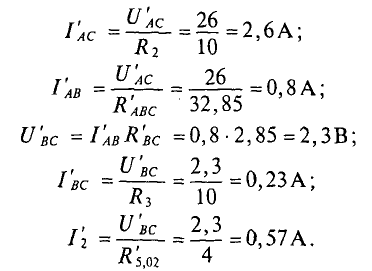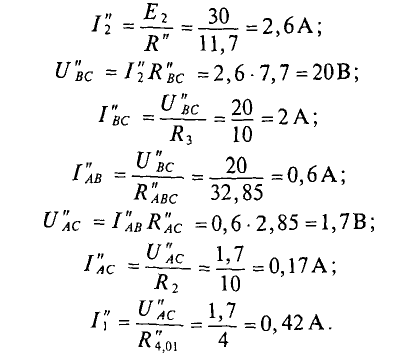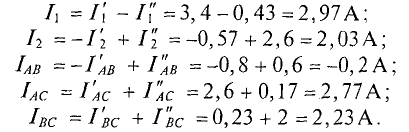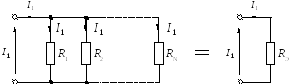Способы преобразования электрических схем

Метод преобразования схем электрических цепей

Метод преобразования схем:

Метод преобразования электрических схем применяют для расчета сложных цепей путем преобразований треугольника сопротивлений в эквивалентную звезду или звезды сопротивлений в эквивалентный треугольник.

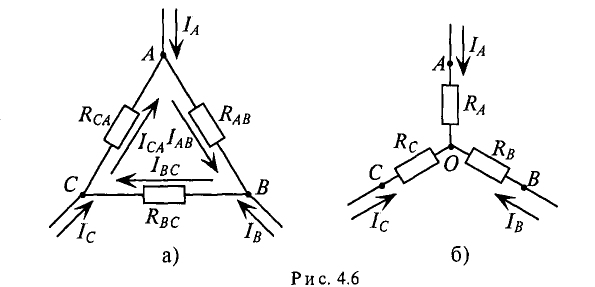
Контур, состоящий из трех сопротивлений

Электрическая цепь, состоящая из трех сопротивлений Ra, Rb и Rc, соединенных в одной узловой точке О, образует звезду сопротивлений (рис. 4.66).

Расчет некоторых сложных цепей значительно упрощается, если соединение звездой в них заменить соединением треугольником или наоборот.

Преобразование схемы должно производиться так, чтобы при неизменном напряжении между точками А, В и С токи 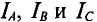звезды и треугольника оставались без изменений.

Треугольник и звезда, удовлетворяющие этому условию, называются эквивалентными.

Для такого преобразования рекомендуется изображать схему цепи без заменяемого треугольника (или звезды), но с обозначенными вершинами А, В, и С и к этим обозначенным вершинам подсоединить эквивалентную звезду (или треугольник).

При замене треугольника эквивалентной звездой сопротивления звезды определяются следующими выражениями:

Таким образом, каждое сопротивление эквивалентной звезды равно отношению произведения двух примыкающих к соответствующей узловой точке сопротивлений треугольника к сумме трех его сопротивлений.

При замене звезды эквивалентным треугольником каждое составление треугольника определяется следующими выражениями:

Каждое сопротивление эквивалентного треугольника равно сумме трех слагаемых: двух примыкающих к соответствующим точкам сопротивлений звезды и отношению произведения этих сопротивлений к третьему сопротивлению звезды.

Пример 4.4

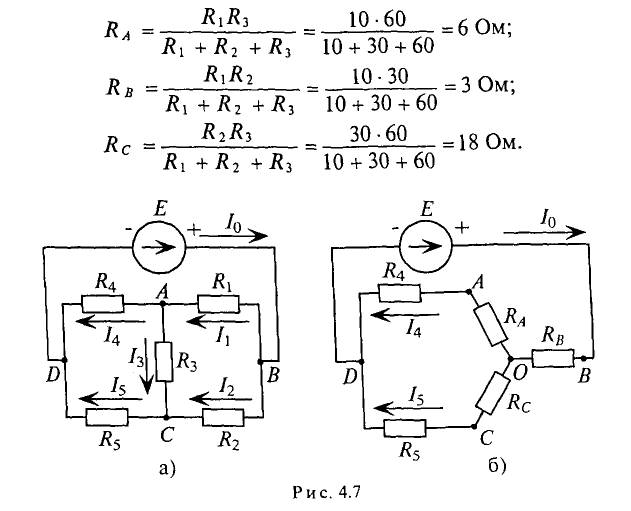
Определить токи во всех ветвях цепи (рис. 4.7а) при следующих сходных данных:

Решение

Для расчета этой цепи заменим треугольник сопротивлений, подключенных к точкам А, В и С, эквивалентной звездой, подученной к тем же точкам (рис. 4.76). Определим величины сопротивлений эквивалентной звезды:

Пример 4.6

Определить токи во всех ветвях цепи, схема которой приведена на рис. 4.8а, если задано:

Решение

Количество ветвей и соответственно различных токов в цепи (рис. 4.8а) равно пяти. Произвольно выбирается направление этих токов.

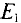
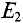
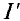
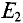
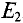
Расчетных схем две, так как в цепи два источника с ЭДС и . Вычисляются частичные токи, созданные в ветвях первым источником . Для этого изображается та же цепь, только вместо — его внутреннее сопротивление Направление частичных токов в ветвях указаны в схеме рис. 4.86.

Вычисление сопротивлений и токов производится методом свертывания.

Первые частичные токи в цепи (рис. 4.86), созданные источником Еи имеют следующие значения:

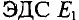
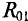
Вычисляются частичные токи, созданные вторым источником. Для этого изображается исходная цепь, в которой источник заменен его внутренним сопротивлением . Направления частичных токов в ветвях указаны на схеме рис. 4.8в. Сопротивления и токи определяются методом свертывания.

Вторые частичные токи в цепи (рис. 4.8в) имеют следующие значения:

Искомые токи в рассматриваемой цепи (рис. 4.8а) определяют алгебраической суммой частичных токов (см. рис. 4.8):

Ток 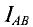имеет знак «минус», следовательно, его направлен противоположно произвольно выбранному, он направлен из точки А в точку В.

Рекомендую подробно изучить предметы:

Электротехника Основы теории цепей

Ещё лекции с примерами решения и объяснением:

• Параллельное соединение генераторов
• Метод узловых и контурных уравнений
• Метод эквивалентного генератора
• Теоремы теории цепей
• Входные и взаимные проводимости
• Преобразование треугольника сопротивлений в эквивалентную звезду
• Метод контурных токов
• Метод свертывания электрической цепи

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

1.6 Преобразования линейных электрических схем

1.6.1 Общие замечания

Расчет сложной цепи может быть значительно облегчен путем эквивалентного преобразования электрических схем.

Целесообразное преобразование обеспечивает:

уменьшение числа узлов в схеме (числа «n»);

уменьшение числа ветвей в схеме (числа «g»).

Указанное, сокращает число расчетных уравнений.

Преобразование схемы имеет две задачи:

свернуть цепь к простой и простыми способами получить решение этой задачи;

развернуть полученное решение до первоначально заданной схемы.

Известно, что электрические цепи можно соединить между собой только тремя способами:

Рассмотрим данные соединения подробнее.

1.6.2 Последовательное соединение

Рисунок 1.18 — Последовательное соединение

Последовательным соединением называется такое при котором через все элементы цепи проходит один и тот же ток.

Согласно схемы имеем:

;

; или

. (1.15)

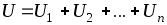
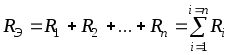
При последовательном соединении сопротивлений общее сопротивление всегда равно их сумме.

Рассмотрим, как распределяются напряжения по элементам:

, таким образом

. (1.16)

На последовательно соединенных сопротивлениях напряжения распределяется прямо пропорционально сопротивлениям.

1.6.3 Параллельное соединение

Рисунок 1.19 — Параллельное соединение

Параллельным соединением сопротивлений называется такое соединений, при котором все сопротивления находятся под воздействием одного и того же напряжения.

Согласно схемы имеем:

;

;

; (1.17)

.

При параллельном соединении сопротивлений складываются величины, обратные сопротивлениям то есть, проводимости.

При параллельном соединении общая проводимость всегда равна сумме проводимостей всех ветвей.

Рассмотрим два наиболее часто встречающихся на практике случая параллельного соединения.

а) Параллельное соединение n одинаковых сопротивлений.

Согласно (1.17), имеем:

;

. (1.18)

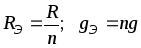
Общее сопротивление n одинаковых, параллельно соединенных сопротивлений, в n раз меньше сопротивления одной ветви, а общая проводимость в n раз больше проводимости одной ветви.

б) Параллельное соединение двух сопротивлений.

Согласно (1.17), имеем:

; ; отсюда получаем

. (1.19)

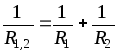
Общее сопротивление двух параллельных ветвей всегда равно произведению сопротивлений на сумму сопротивлений этих ветвей.

Рассмотрим, как распределяются токи в двух ветвях:

;

; . (1.20)

, откуда

. (1.21)

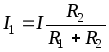
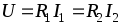
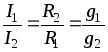
В параллельных ветвях токи обратно пропорциональны сопротивлениям или прямо пропорциональны проводимостям ветвей.

1.6.4 Смешанное соединение

Рисунок 1.20 — Смешанное соединение сопротивлений

Смешанным соединением сопротивлений называется такое соединение, при котором действуют одновременно и параллельное и последовательное соединение.

Согласно схеме имеем

Рисунок 1.21 — Промежуточное преобразование смешанного соединения

и далее,

. (1.22)

Отсюда найдем токи:

; (1.23)

; (1.24)

. (1.25)

В результате преобразования удалось решить разветвленную цепь простыми средствами, в нашем случае, даже без составления уравнений.

Следует иметь в виду, что при преобразовании схемы, состоящей только из сопротивлений (ветви не имеют источников энергии), мощность в эквивалентной схеме равна мощности в заданной неразветвленной цепи.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

Эквивалентные преобразования в электрических цепях

При расчёте электрических цепей грамотно проведённые преобразования позволяют уменьшить число уравнений, описывающих работу схемы. Далее приведены основные эквивалентные преобразования.

Воспользуйтесь программой онлайн-расчёта электрических цепей. Программа позволяет рассчитывать электрические цепи по закону Ома, по законам Кирхгофа, по методам контурных токов, узловых потенциалов и эквивалентного генератора, а также рассчитывать эквивалентное сопротивление цепи относительно источника питания.

Последовательное соединение пассивных элементов

Пример схемы приведён на рис. 1.

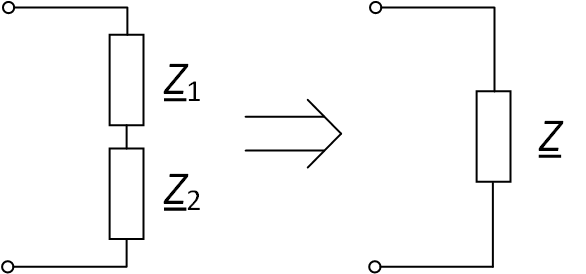
Рис. 1. Преобразование последовательно соединённых элементов

Эквивалентное сопротивление определяется по формуле

В общем случае при последовательном соединении N элементов

Параллельное соединение пассивных элементов

Пример схемы приведён на рис. 2.

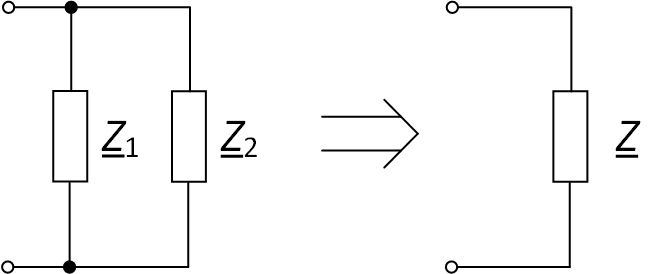
Рис. 2. Преобразование параллельно соединённых элементов

Эквивалентное сопротивление определяется по формуле

Параллельное соединение большого количества ветвей

Пример схемы приведён на рис. 3.

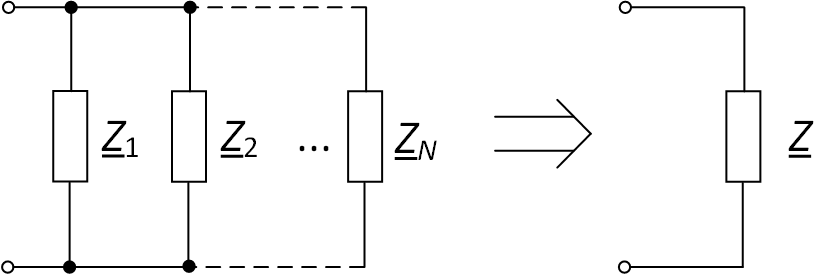
Рис. 3. Преобразование параллельно соединённых ветвей

Эквивалентное сопротивление определяется по формуле

Параллельное соединение ветвей с источниками ЭДС

Пример схемы приведён на рис. 4.

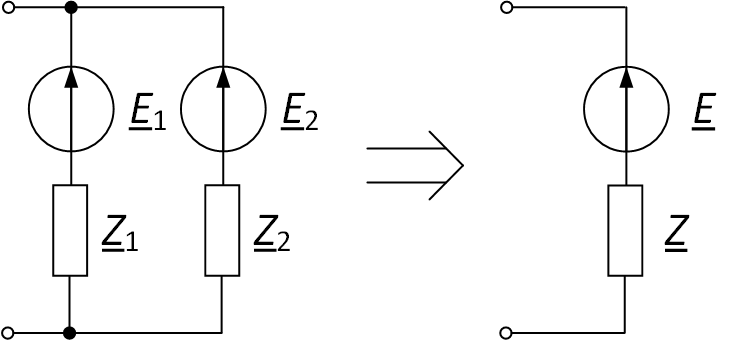
Рис. 4. Преобразование параллельно соединённых ветвей с источниками ЭДС

Эквивалентное сопротивление определяется по формуле

Эквивалентная ЭДС определяется по формуле

В общем случае при параллельном соединении N ветвей с источниками ЭДС эквивалентное сопротивление определяется по формуле

Эквивалентная ЭДС при параллельном соединении N ветвей определяется по формуле

Преобразование источника ЭДС в источник тока

Пример схемы приведён на рис. 5.

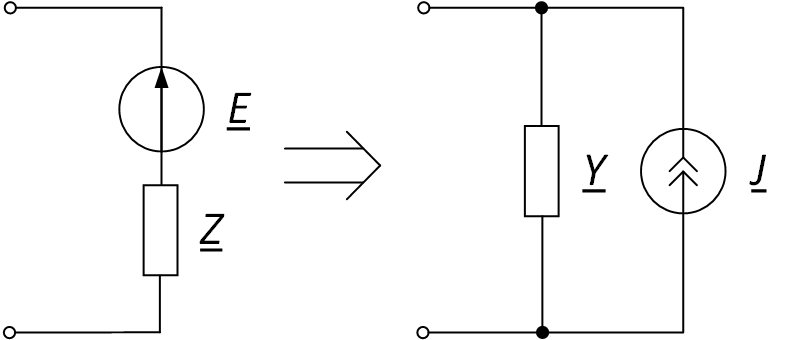
Рис. 5. Преобразование источника ЭДС в источник тока

Сила тока источника тока определяется по формуле

Проводимость ветви, параллельной источнику току, определяется по формуле

Преобразование источника тока в источник ЭДС

Пример схемы приведён на рис. 6.

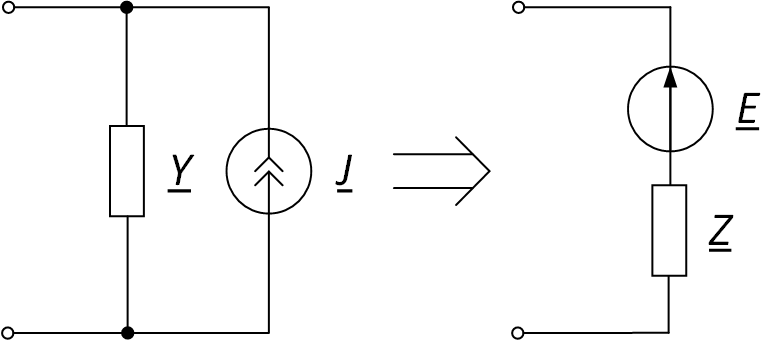
Рис. 6. Преобразование источника тока в источник ЭДС

ЭДС определяется по формуле

Сопротивление определяется по формуле

Преобразование звезды сопротивлений в треугольник

Пример схемы приведён на рис. 7.

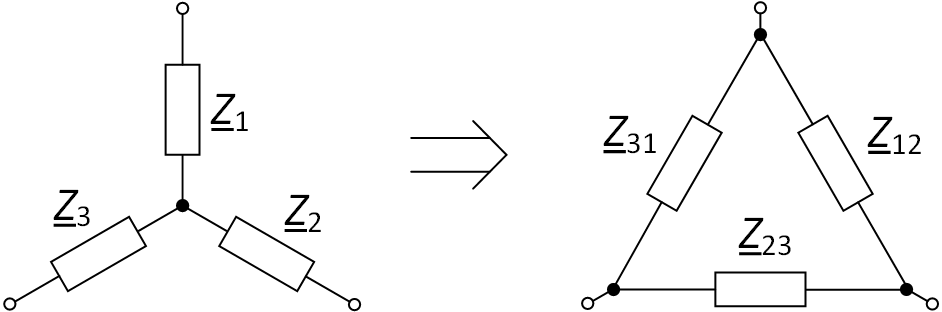
Рис. 7. Преобразование звезды в треугольник

Сопротивления треугольника определяются по формулам

Калькулятор преобразования звезды сопротивлений в треугольник

Преобразование треугольника сопротивлений в звезду

Пример схемы приведён на рис. 8.

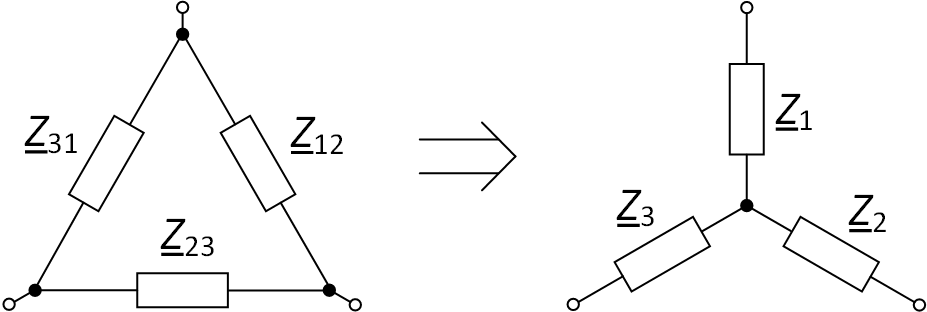
Рис. 8. Преобразование треугольника в звезду

Сопротивления звезды определяются по формулам

Калькулятор преобразования треугольника сопротивлений в звезду

Список использованной литературы

1. Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.

Рекомендуемые записи

На сайте появилась программа для расчёта установившихся режимов электрических цепей по законам ТОЭ. На настоящий…

При расчёте электрических цепей, в том числе для целей моделирования, широко применяются законы Кирхгофа, позволяющие…

При исследовании электрических цепей и моделировании часто пользуются векторными диаграммами токов и напряжений. Под векторной…

Источник