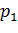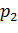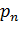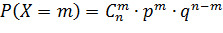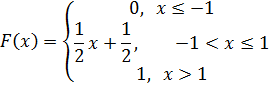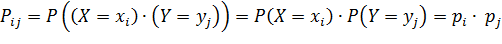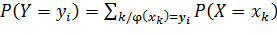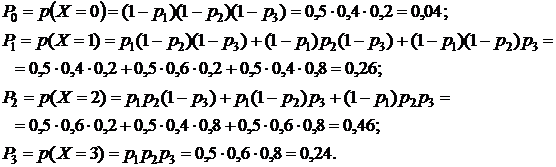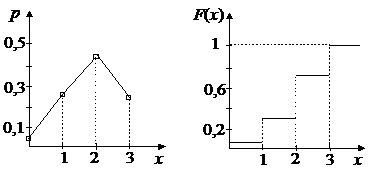Случайные величины и способы их описания
1. Дискретные и непрерывные случайные величины.
Среди задач, решаемых ТВ, очень много таких, в которых исход опыта выражается некоторым числом.
Случайной величиной (СВ) называется величина, которая при каждом осуществлении опыта принимает то или иное числовое значение, заранее неизвестно, какое именно.
Обозначение: X, Y, Z,… — случайные величины. Возможные значения случайных величин: x, y, z,… Каждой случайной величине соответствует некоторое множество возможных значений.
Примеры: 1) Опыт — бросание игрального кубика. СВ — число выпавших очков на верхней грани. Возможные значения: 1,2,3,4,5,6.
2) Покупается n лотерейных билетов. СВ – число выигрышей. Возможные значения: 0,1,2,…,n
3) Электрическая лампочка испытывается на длительность горения. СВ – длительность горения лампочки. Возможные значения: любое неотрицательное число.
4) Некто приходит на станцию метро и ожидает поезда. СВ – время ожидания ближайшего поезда. Возможные значения: [0;2мин].
Из примеров видно, что СВ различаются по множеству возможных значений.
Случайная величина называется дискретной(ДСВ), если множество её возможных значений счетно (в частности конечно), то есть может быть занумеровано. Примеры 1, 2 – ДСВ.
Случайная величина называется непрерывной (НСВ), если её возможные значения сплошь заполняют некоторый промежуток (или несколько промежутков) числовой оси. Примеры 3, 4 – НСВ. Различные СВ могут иметь одно и то же множество возможных значений. Поэтому для полного описания СВ необходимо знать, как часто СВ принимает то или иное свое значение.
2. Законы распределения СВ.
Законом распределения СВ называется всякое соотношение, устанавливающее связь между возможными значениями СВ и соответствующими им вероятностями.
Закон распределения ДСВ.
Для ДСВ закон распределения можно задать таблично, аналитически и графически.
1) Табличный способ – это таблица, в которой перечислены в порядке возрастания все возможные значения СВ и соответствующие вероятности принятия этих значений.
| ||||||||||||
 ) |
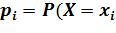Эта таблица называется ряд распределения ДСВ.
(так как события X=
; X=
; …; X=
образуют полную группу)
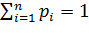
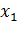
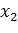
Если множество возможных значений случайной величины бесконечно (но счетно), то ряд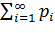 
сходится, и его сумма = 1.
Опыт — бросание игрального кубика. СВ — число выпавших очков на верхней грани. Ряд распределения:
| хi | ||||||
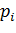 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
2) Аналитический способ – задаётся формула, по которой находится вероятность каждого возможного значения случайной величины.
Например, если опыт проводится по схеме Бернулли, то вероятности возможных значений могут быть найдены по формуле: 
3) Графический способ.
Закон распределения можно изобразить графически, если по оси абсцисс откладывать значения СВ, а по оси ординат – их вероятности. Соединив точки (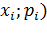
отрезками прямых, получим ломаную, называемую многоугольником или полигоном распределения вероятностей.
Закон распределения НСВ.
Под законом распределения НСВ понимают задание функции f(x), называемой плотностью распределения вероятности, такой, что вероятность попадания СВ в промежуток [a;b] равна P(a≤X≤b)=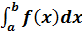
.
Свойства плотности вероятности:
1) f(x)≥0 (следует из аксиом вероятности);
2) 
(вероятность достоверного события);
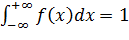
3) P(X=a)=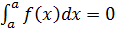 
(для НСВ говорят о вероятности попасть в промежуток, вероятность попасть в точку принимают = 0) =>
P(a ≤ X ≤ b) = P(a 
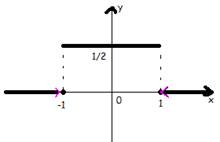
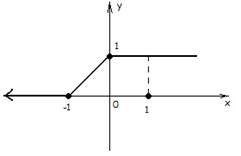
4) F(x) – неубывающая функция;
F(x)=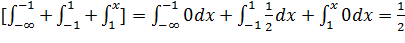
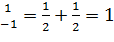
x |
.
4. Операции над СВ.
Введём математические операции над ДСВ. Для НСВ вводится аналогично.
Пусть X — ДСВ, принимающая возможные значения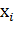 
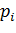
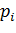
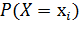
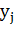
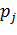
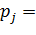
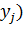
с вероятностями , то есть =
. Пусть Y — ДСВ, принимающая возможные значения 
с вероятностями 
, то есть 
P(Y=
.
Произведением ДСВ X и постоянной величины С, называется ДСВ С∙Х, которая принимает возможные значения C∙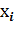
с теми же вероятностями 
Суммой двух ДСВ X и Y называется ДСВ X+Y, которая принимает возможные значения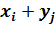 
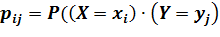
с вероятностями 
).
Произведением двух ДСВ X и Y называется ДСВ X∙Y, которая принимает возможные значения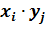 
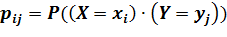
с вероятностями 
.
Две СВ называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая случайная величина.
Для независимых СВ X и Y выполняется:
Пусть дана ДСВ Х и функция φ(x), определенная на всей вещественной оси, тогда функцией от ДСВ Х называется ДСВ Y= φ(Х), которая принимает возможные значения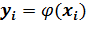 
с вероятностями 
(где сумма по всем k таким, что значения φ(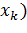
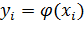
совпадают со значением 
).
Пример: пусть даны дискретные случайные величины
| 0,4 | 0,6 |
| -1 | |
| 0,3 | 0,7 |
Тогда ДСВ 5X будет иметь ряд распределения:
Источник
Способы представления дискретной случайной величины
Случайные величины
Определение и виды случайных величин
Очень часто на практике приходится иметь дело с величинами, значения которых нельзя предсказать заранее. Такими величинами являются, например, число клиентов, обратившихся в банк в течение дня, количество попаданий в мишень при нескольких выстрелах, расстояние от точки попадания до центра мишени, количество осадков за определенный промежуток времени и т. д. На каждую из этих величин действует большое количество мелких факторов, которые трудно, иногда и невозможно, а иногда и не нужно учитывать по отдельности. Например, на полет снаряда, кроме основных — калибра орудия, величины заряда и наводки — влияют скорость и направление ветра, плотность воздуха, зависящая от температуры, осадки и т. п. Поскольку сами эти факторы не остаются неизменными, то и их влияние на определяемую в опыте величину будет также меняться. В результате от опыта к опыту будет получаться несколько иное значение измеряемой величины.
Случайной называется переменная величина, значения которой зависят от случайного исхода опыта.
Некоторые из случайных величин, например, число клиентов в банке, количество попаданий в мишень могут принимать отдельные, изолированные значения, которые можно перечислить.
Случайная величина, которая может принимать значения некоторой конечной или бесконечной числовой последовательности, называется дискретной (краткое обозначение ДСВ).
Случайная величина, которая может принимать любые значения из некоторого промежутка или промежутков, называется непрерывной (краткое обозначение НСВ).
Непрерывной случайной величиной является, например, количество осадков или расстояние от точки попадания до центра мишени.
Случайные величины принято обозначать большими латинскими буквами 
. Чтобы описать случайную величину, нужно не только знать, какие значения она принимает, но и как часто, т. е. с какой вероятностью встречаются те или иные значения. В опыте случайная величина обязательно примет одно из своих значений, поэтому полная (суммарная) вероятность равна 1. То, как эта полная вероятность поделена между различными значениями случайной величины, называется распределением случайной величины.
Способы описания распределения для ДСВ и НСВ несколько различны, поэтому рассмотрим их отдельно.
Способы представления дискретной случайной величины
Законом распределения ДСВ называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Таблица, в которой представлены значения 
случайной величины 
и соответствующие им вероятности 
(т. е. вероятности того, что примет значение, равное 
), называется рядом распределения. Если в таблице учтены все возможные значения 
, то должно выполняться условие
.
Информация о распределении, представленная на графике точками с координатами (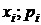 
) и соединяющей их ломаной, называется многоугольником (полигоном) распределения.
Вероятность того, что случайная величина примет значение, меньшее 
, называется функцией распределения 
, т. е. 
. Для ДСВ
.
Пример. Батарея состоит из 3 орудий. Вероятность попадания в цель при одном выстреле для первого орудия 
= 0,5; для второго 
= 0,6; для третьего — 
= 0,8. Все орудия делают по одному выстрелу. Охарактеризовать случайную величину Х — число попаданий в цель.
Очевидно, что Х может принять одно из четырех значений: 0, 1, 2, 3 .
= 0, если ни одно орудие не попадет;
= 1, если попадет одно орудие (либо первое, либо второе, либо третье); = 2, если попадут два орудия: либо первое и второе, либо первое и третье, либо второе и третье;
= 3, если попадут все три орудия.
Сделаем проверку: 
.
Выпишем ряд распределения
 | ||||
 | 0,04 | 0,26 | 0,46 | 0,24 |
Полигон распределения представлен на рисунке. Функция распределения представлена таблицей и графиком.
 |  |  |  |  |  |
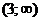 | 0,04 | 0,3 | 0,76 |
Данный пример иллюстрирует следующие свойства функции распределения ДСВ (которые можно легко доказать, учитывая, что вероятность любого события заключена в пределах от 0 до 1).
1) – ступенчатая разрывная функция;
2) – неубывающая функция (т. е. либо возрастает, либо постоянна);
3) = 0, для всех 
, где 
– наименьшее из всех значений ;
4) = 1, для всех 
, где 
– наибольшее из всех значений .
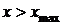
Приведенные характеристики дают полное и ясное представление о случайной величине. Однако, в случае, когда ДСВ имеет много значений ( десятки, сотни и т. д. ) они будут очень громоздкими и требуют много места. Кроме того, во многих практических задачах вовсе нет необходимости так подробно описывать случайную величину.
Источник
