4. Представление пространственных форм
Во многих приложениях машинной графики возникает потребность в представлении трехмерных форм: при проектировании самолетов, при восстановлении трехмерных тел по изображениям их поперечных сечений, построенных с помощью машинной томографии, при автоматической сборке и во многих других. Нам уже известно, как изображаются пространственные объекты, когда их удается представить в виде последовательности отрезков прямых, заданных в мировых координатах. Совокупность отрезков не является адекватным описанием объекта, поскольку отрезки сами по себе не определяют поверхностей. В то же время информация о поверхностях необходима для проведения вычислений, связанных со стиранием скрытых частей изображения, для определения объемов и т. д. Таким образом, мы приходим к выводу, что для описания трехмерных форм необходимы поверхности – примитивы более высокого уровня, чем отрезки.
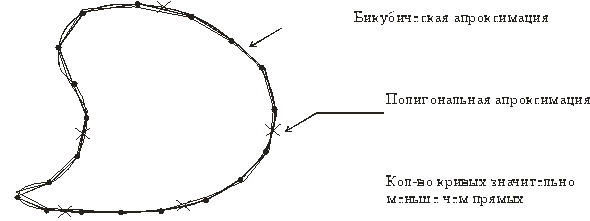
Мы остановим внимание на двух широко распространенных трехмерных представлениях поверхностей в пространстве: полигональных сетках и параметрических бикубических кусках. Полигональной сеткой является совокупность связанных между собой плоских многоугольников. Наружную форму большинства зданий можно легко и естественно описать с помощью полигональной сетки (так же, как мебель и комнаты). Полигональные сетки применяются также для представления объектов, ограниченных криволинейными поверхностями. Однако недостатком этого метода является его приблизительность. Видимые ошибки в таком представлении можно сделать сколь угодно малыми, используя все большее число многоугольников для улучшения кусочно-линейной аппроксимации объекта, но это приведет к дополнительным затратам памяти и вычислительного времени для алгоритмов, работающих с таким представлением.
Параметрические бикубические куски описывают координаты точек на искривленной поверхности с помощью трех уравнений (по одному для х, у и z ). Каждое из уравнений имеет две переменные (два параметра), причем показатели степени при них не выше третьей (отсюда название бикубический). Границами кусков являются параметрические кубические кривые. Для представления поверхности с заданной точностью требуется значительно меньшее число бикубических кусков, чем при аппроксимации полигональной сеткой. Однако алгоритмы для работы с бикубическими объектами существенно сложнее алгоритмов, имеющих дело с многоугольниками.
При использовании обоих методов трехмерное тело представляется в виде замкнутой поверхности.
Источник
Представление пространственных форм
До сих пор рассматривалась возможность построения 3-х мерных линейчатых объектов на основе примитивов в виде отрезков. Однако возникают ситуации (особенно автоматизированное программирование), когда необходим вывод 3-х мерных форм:
-описание заданной формы (пластилиновой);
-процесс творческого создания формы объекта;
Представление пространственной формы с помощью набора из 12 отрезков (неоднозначность пространственного отображения формы)
В общем случае, пространственную форму можно создать из примитивов более высокого уровня (чем 2-х мерная графика) => плоскости сферы и т.п.
При автоматизированном проектировании возникает проблема максимальноточного отображения формы (определение объемов, сечений, стирание скрытых областей), т.е. возникаетпроблемагеометрическогомоделированияобъектов.
Используются два способа изображения поверхностей в пространстве:
-параметрические бикубические сплайны
П.С. – это совокупность связанных многоугольников.
Недостаток: приблизительность моделирования объекта. При более детальной прорисовке необходимы большие вычислительные и временные затраты ЭВМ.
Для сложных объектов:
«–»большой объем памяти
2.Параметрические бикубические поверхности.
Координаты точек искривленных поверхностей описываются с помощью 3-х уравнений (для x, y и z)
Каждое уравнение имеет две переменные (би), показатель степени не выше 3-ей (куб). Границы поверхностей – это параметрические кубические кривые.
Преимущество: значительное снижение кусков аппроксимации, однако более сложная алгоритмизация.
«+»малый объем памяти
«-»время вычисления сплайнов
Методы описания полигональных сеток.
1.Явное задание многоугольников.
Многоугольник Р описывается:
P – список координат вершин в порядке обхода многоугольника.
-двойная прорисовка ребер
-для поиска многоугольников с одной вершиной необходимо сравнение пар ребер всех
-неоднозначность определения вершин при сравнении координат (потеря точности)
2.Указатели в список вершин.
Узел сетки запоминается лишь один раз в списке вершин:
Многоугольник определяется ссылкой на элемент списка.
Преимущество: экономия памяти за счет однократного описания каждой вершины. Кроме того координаты вершин легко меняются.
Недостаток: трудно искать многоугольники с одинаковыми ребрами.
3.Явное задание ребер.
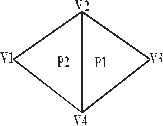
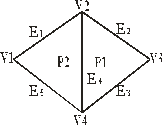
Имеется список вершин V. Имеется список Е, каждый элемент которого описан тетраэдр.
P1 – многоугольник 1
P2 – многоугольник 2
Если ребро принадлежит одному многоугольнику, то одна из ссылок а – пуста.
Многоугольник определяется как ссылка на ребре Р=(Е1. Еn)
E1=(V1,V2,P1,l )
E2=(V2,V3,P2,l )
E3=(V3,V4,P2, l)
E5=(V4,V1,P1,l )
P2=(E1,E3,E4) E4 – не прорисовывается т.к. ссылка на P1
l = пусто
Вычеркиваются все ребра.
Для определения произвольной точки внутри многоугольника на плоскости можно пользоваться системой уравнений:
Ax+By+Cz+D=0 – уравнение плоскости
Уравнения решаются относительно x,y,z.
Где: коэффициенты A,B,C,D определяются для плоскости по трем вершинам.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Представление пространственных форм.
Необходимые представления объёмного объекта возникают в двух случаях:
1) Объект уже существует и его требуется описать.
2) Имеется приблизительная модель объекта.
В каждом случае есть свои особенности. В первой ситуации точно описать его возможно только в том случае, если он состоит из математических поверхностей. Встречается это очень редко. Если объект нельзя представить как совокупность математических поверхностей, то для его полного описания требуется бесконечное количество точек. Такое описание никто позволить не может. В этом случае на поверхности объекта выбирается ряд точек, которые называются базовыми, затем подбирается такое описание, которое наиболее точно или с нужной степенью приближения подходит к данному объекту. Приближающие поверхности всегда проходят через базовую точку. Чем более грубо мы выполняем приближение, тем более простую модель мы получаем.
Во втором случае наиболее важна возможность организации интерактивного режима. Характерна для систем автоматизированного проектирования. Конструктор вначале создаёт эскиз детали, затем в диалоговом режиме достигает каких-либо параметров.
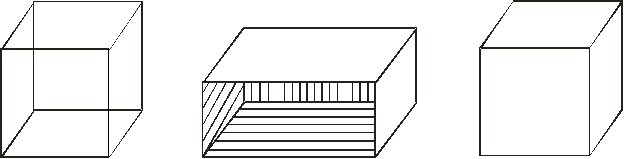
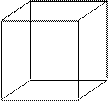
Для 3D объекта описание в виде отрезков является неверным. Что может реально такая картинка представлять?
1) Кубик из проволоки.
2) Кубик со всеми 6-ю гранями.
3) Фигура, не имеющая двух граней.
 |
В описании 3D фигур вводятся поверхности. Вообще говоря, сложность математического аппарата для задания форм поверхности теоретически ничем не ограничена. Практика показала, что достаточно использовать либо полигональные сетки (из кусков плоской поверхности), либо параметрические кубические уравнения, причём надо ограничиться уравнениями третьего порядка. Если использовать уравнения четвёртого порядка, то мы получим несущественный выигрыш в качестве, но сложность математического аппарата возрастёт в несколько порядков.
Полигональная сетка.
 |
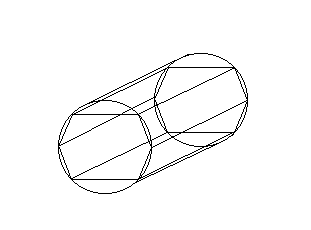Представляет собой совокупность плоских многоугольников. Многоугольники связаны между собой. Количество вершин у многоугольников не ограничено. Способ задания является неточным. Погрешности существенны для тел сложной формы, хотя теоретически любой сложности тело можно представить отрезками плоскостей.
Например, шестигранник ещё не похож на цилиндр, а 12-гранник его уже больше напоминает. Чем больше плоскостей, тем точнее мы подгоним фигуру. Следует помнить, что чем точнее приближение, тем дольше происходит математическая обработка описания и тем больше требуется использовать памяти.
Параметрические кубические прямые описывают поверхность через уравнения третьего порядка.
f(x, y, z), причём уравнений записывается три. f – это многочлен третьего порядка.
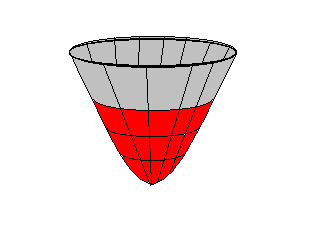
Существует целый набор способов представления. Число участков сразу же снижается, сложность вычислений возрастает. Всё равно сложное тело описать одним уравнением не получится. Как описывать полигоны?
Например, здесь 2 куска поверхности с разными описаниями, а вообще их может быть и больше.
 |
Способы описания полигональной сетки:
1) Явное задание многоугольников.
2) С помощью указателей в списке вершин.
1. P – многоугольник. P=((x1, y1, z1), (x2, y2, z2), (x3, y3, z3), … , (xn, yn, zn)). Причём точки в перечислении записываются строго в порядке обхода многоугольника. Последняя n-я точка соединяется с первой в записи. Фигура – это совокупность многоугольников.
2 3 4
 |
1 9 7
II
5
– мы прорисовывали 2 раза. Это не модно. Координаты точки 7 входят несколько раз. Мы дублируем одни и те же данные. Точка, участвующая в описании двух сторон будет записываться дважды, трёх сторон – трижды и так далее. Объём хранимой информации явно завышен. Существуют математические способы определения общих участков пространственных кривых, но количество сравнений для выполнения таких отсечений становится неоправданно большим. Также редактировать такие ссылки очень сложно. Способ этот громоздкий, но легко доступный для понимания.
2. 1) Составляется предварительный список вершин, не обязательно по возрастанию номеров:
В этом списке ни одна точка не повторяется дважды. Затем ориентируясь на номер записи в списке вершин описывают полигон.
Сами записи проще, занимают меньший объём памяти, гораздо проще редактировать фигуру.
z
 |
2 3
8 5 x
1 4
Источник
Представление пространственных форм
Во многих приложениях машинной графики возникает потребность в представлении трехмерных форм: при проектировании самолетов, при восстановлении трехмерных тел по изображениям их поперечных сечений, построенных с помощью машинной томографии, при автоматической сборке и во многих других. Нам уже известно, как изображаются пространственные объекты, когда их удается представить в виде последовательности отрезков прямых, заданных в мировых координатах. Совокупность отрезков не является адекватным описанием объекта, поскольку отрезки сами по себе не определяют поверхностей. В то же время информация о поверхностях необходима для проведения вычислений, связанных со стиранием скрытых частей изображения, для определения объемов и т. д. Таким образом, мы приходим к выводу, что для описания трехмерных форм необходимы поверхности – примитивы более высокого уровня, чем отрезки.
Мы остановим внимание на двух широко распространенных трехмерных представлениях поверхностей в пространстве: полигональных сетках и параметрических бикубических кусках. Полигональной сеткой является совокупность связанных между собой плоских многоугольников. Наружную форму большинства зданий можно легко и естественно описать с помощью полигональной сетки (так же, как мебель и комнаты). Полигональные сетки применяются также для представления объектов, ограниченных криволинейными поверхностями. Однако недостатком этого метода является его приблизительность. Видимые ошибки в таком представлении можно сделать сколь угодно малыми, используя все большее число многоугольников для улучшения кусочно-линейной аппроксимации объекта, но это приведет к дополнительным затратам памяти и вычислительного времени для алгоритмов, работающих с таким представлением.
При втором способе описания трехмерных форм поверхность может быть разбита на куски, каждый из которых будет описан параметрическим бикубическим уравнением. Поэтому такие поверхности называют параметрические бикубические поверхности.
Рис. 7.1. Параметрический бикубический кусок
Параметрические бикубические куски (рис. 7.1), из которых состоят эти поверхности, описываются координатами точек с помощью трех уравнений (по одному для х, у и z). Каждое из уравнений имеет две переменные (два параметра), причем показатели степени при них не выше третьей (отсюда название бикубический). Уравнение для X будет выглядеть следующим образом:
Аналогично записываются уравнения для Y и Z.
Границами кусков являются параметрические кубические кривые. Для представления поверхности с заданной точностью требуется значительно меньшее число бикубических кусков, чем при аппроксимации полигональной сеткой. Однако алгоритмы для работы с бикубическими объектами существенно сложнее алгоритмов, имеющих дело с многоугольниками.
При использовании обоих методов трехмерное тело представляется в виде замкнутой поверхности.
Полигональные сетки
Полигональная сетка представляет собой совокупность ребер, вершин и многоугольников. Вершины соединяются ребрами, а многоугольники рассматриваются как последовательности ребер или вершин. Сетку можно представить несколькими различными способами, каждый из них имеет свои достоинства и недостатки. Для оценки оптимальности представления используют следующие критерии:
· Объем требуемой памяти;
· Простота идентификации ребер, инцидентных вершине;
· Простота идентификации многоугольников, которым принадлежит данное ребро;
· Простота процедуры поиска вершин, образующих ребро;
· Легкость определения всех ребер, образующих многоугольник;
· Простота получения изображения полигональной сетки;
· Простота обнаружения ошибок в представлении (например, отсутствие ребра или вершины или многоугольника).
Рассмотрим подробнее три способа описания полигональных сеток.
Источник
