Способы представления графов презентация

Презентация по дискретной математике «Представление графов)

Описание презентации по отдельным слайдам:

Представление графа списком пар вершин 6 5 Список пар вершин 1 2 3 4 6 5 4 3 2 1 1 1 3 3 5 5 6 2 3 2 4 4 6 5 1 1 1 2 2 3 4 4 5 2 3 5 3 5 4 5 6 6

6 5 Матрицы смежности графов А(G)= А(G)= 5 4 3 2 1 1 2 3 4 6 1 2 3 4 5 6 1 0 1 1 0 0 0 2 0 0 0 0 0 0 3 0 1 0 1 0 0 4 0 0 0 0 0 0 5 0 0 0 1 0 1 6 0 0 0 0 1 0 1 2 3 4 5 6 1 0 1 1 0 1 0 2 1 0 1 0 1 0 3 1 1 0 1 0 0 4 0 0 1 0 1 1 5 1 1 0 1 0 1 6 0 0 0 1 1 0

Представление взвешенного графа а b c h f d e 2 5 1 6 4 6 8 2 2 3 Матрица смежности a b c d e f h a 0 2 0 2 3 0 0 b 0 0 5 0 0 0 0 c 0 0 0 0 0 0 6 d 0 0 1 0 2 0 4 e 0 0 0 0 0 8 0 f 0 0 0 0 0 0 6 h 0 0 0 0 0 0 0

Представление графа в виде матрицы инциденций 1 2 3 5 4 с а b d f e h a b c d e f h 1 1 0 1 0 0 0 1 2 1 1 0 0 0 0 0 3 0 1 1 1 1 0 0 4 0 0 0 0 1 1 1 5 0 0 0 1 0 1 0

Граф и матрица векторов смежности 1 2 3 5 4 1 2 3 4 0 2 1 4 0 0 3 1 2 4 5 4 1 3 5 0 5 4 0 0 0

Задача 1 Охарактеризуйте граф. Назовите все ребра. Назовите все дуги. Укажите вершины инцидентные ребру 6; 2. Укажите ребра инцидентные вершине a; f. Назовите смежные вершины, ребра, дуги. Запишите ребро (дугу) 2; 3; 5; 7 через вершины. a b c d f 1 2 3 4 6 5 7

Задача 2 Постройте граф с вершиной, имеющей степень 3. Постройте орграф с полустепенью исхода и полустепенью захода равным 2. Сколько ребер в полном графе с 10-ю вершинами. Постройте неполный граф с 6-ю вершинами. Постройте дополнение графа и полный граф.

Задача 3 Найти сумму степеней вершин графа

Задача 4 Найти сумму полустепеней исхода и полустепеней захода орграфа.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 832 человека из 77 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 297 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 609 человек из 76 регионов

Ищем педагогов в команду «Инфоурок»

Презентация по дискретной математике «Представление графов» подготовлена для изучения нового материала по теме «Теория графов» для студентов СПО специальности «Программирование в компьютерных системах».

В презентации представлены различные способы представления графов в виде пар вершин, матриц, рассматриваются различные типы графов (орграфы, неориентированный, двудольные, взвешенные и др.). Слайды содержат примеры графический изображений графов.

Материал может использоваться при объяснении нового материала, повторении, самоподготовке студентов к практическим занятиям.

Номер материала: 536582

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

В Осетии студенты проведут уроки вместо учителей старше 60 лет

Время чтения: 1 минута

В Минпросвещения предложили организовать телемосты для школьников России и Узбекистана

Время чтения: 1 минута

Путин попросил привлекать родителей к капремонту школ на всех этапах

Время чтения: 1 минута

В Москве запустили онлайн-проект по борьбе со школьным буллингом

Время чтения: 2 минуты

Руководители управлений образования ДФО пройдут переобучение в Москве

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Презентация по информатике на тему «Графы»(11 класс)

Описание презентации по отдельным слайдам:

Цели и задачи урока: * расширить представление о видах информационных моделей * сформировать представление о графах как наглядном средстве представления и состава системы * развивать умения построения схем. * из 16

Вспомним! Что такое модель? Что такое информационная модель? Где применяются схемы, чертежи? * из 16

Вспомним! С помощью каких информационных моделей можно отразить отношения между людьми? Как показать дороги и расстояния между городами? Способна ли информатика показать такие отношения? * из 16

Что такое граф? Какие бывают графы? Где встречаются графы в повседневной жизни? * из 16

Неориентированный граф — граф, вершины которого соединены ребрами. С помощью таких графов могут быть представлены схемы двухсторонних (симметричных) отношений. Граф, отражающий отношение «переписываются» между объектами класса «дети» * из 16

Ориентированный граф — граф, вершины которого соединены дугами. С помощью таких графов могут быть представлены схемы односторонних отношений. Маша Юра Аня Витя Коля Граф, отражающий отношение «пишет письма». * из 16

граф, у которого вершины или рёбра (дуги) несут дополнительную информацию (вес). Москва, 1147 Переславль Залесский, 1152 Владимир, 1108 Взвешенный граф — 1182 158 127 * из 16

Постройте взвешенный граф, соответствующей таблице. Что называется взвешенным графом? Как обозначим вершины? Сколько будет вершин? Как обозначим отношения между вершинами? A B C D A 4 5 B 4 3 6 C 5 3 D 6 * из 16

A B C D A 4 5 B 4 3 6 C 5 3 D 6 * из 16

A B C D E 1) 2) A C E B D 1 3 4 1 1 1 1 2 3 4 . Укажите схему, соответствующую таблице. A B C D E A 1 4 1 B 1 3 C 4 2 D 3 E 1 2 * из 16

1.В таблице приведена стоимость перевозок между соседними железнодорожными станциями. Укажите схему, соответствующую таблице. * из 16

3. Грунтовая дорога проходит последовательно через населенные пункты А, В, С, D. При этом длина дороги между А и В равна 80 км, между В и С — 50 км, между С и D — 10 км. Между А и С построили новое асфальтовое шоссе длиной 40 км. Оцените минимально возможное время движения велосипедиста из пункта А в пункт В, если его скорость по грунтовой дороге — 20 км/ч, по шоссе — 40 км/ч. 1) 1 час 2) 1,5 часа 3) 3,5 часа 4) 4 часа * из 16

2 В таблице приведена стоимость перевозки грузов между населенными пунктами. Укажите схему, соответствующую таблице. * из 16

4 В таблице приведена стоимость перевозки одной партии груза между населенными пунктами. Определите минимальную стоимости перевозки двух партий груза из пункта В в пункт С. 1)7 2)8 3)10 4)14 * из 16

Ответ. Вариант 4. Соответствующий граф представлен на приведенном рисун­ке. Минимальный по стоимости путь В — А — Е — D — С. Стоимость перевозки одной партии 3 + 1 + 1 + 2 = 7. Стоимость перевозки двух партий — 14. * из 16

5 Андрей, Борис, Виктор и Григорий после возвращения из спортивного лагеря подари­ли на память друг другу свои фотографии. Причем каждый мальчик подарил каждому из своих друзей по одной фотографии. Сколько всего фотографий было подарено? * из 16

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 832 человека из 77 регионов

Курс профессиональной переподготовки

Математика и информатика: теория и методика преподавания в образовательной организации

• Сейчас обучается 598 человек из 75 регионов

Курс повышения квалификации

Современные педтехнологии в деятельности учителя

• Курс добавлен 23.09.2021
• Сейчас обучается 47 человек из 23 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДВ-064266

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

В Минпросвещения предложили организовать телемосты для школьников России и Узбекистана

Время чтения: 1 минута

В Москве запустили онлайн-проект по борьбе со школьным буллингом

Время чтения: 2 минуты

Путин попросил привлекать родителей к капремонту школ на всех этапах

Время чтения: 1 минута

Минобрнауки разработало концепцию преподавания истории российского казачества

Время чтения: 1 минута

В российских школах оборудуют кабинеты для сообщества «Большой перемены»

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Презентация «Графы»

Содержимое разработки

Графом на плоскости называется конечное множество точек плоскости , некоторые из которых соединены линиями. Эти точки называют вершинами графа , а соединяющие их линии – ребрами. Примерами графов могут служить любая карта дорог , электросхема , чертеж многоугольника и т.д.

Теория графов возникла в 1736г. , когда Леонард Эйлер опубликовал первую статью о графах.

Эйлера называют идеальным математиком 18 века.

В этом году исполнилось 300 лет со дня рождения Леонарда Эйлера .

Эйлер принадлежит к числу гениев, чьё творчество стало достоянием всего человечества. До сих пор школьники всех стран изучают тригонометрию и логарифмы в том виде, какой придал им Эйлер.

Леонард Эйлер был избран академиком

в восьми странах мира. Он оставил важнейшие труды по самым различным отраслям математики, механики, физики, астрономии и по ряду прикладных наук. Трудно даже перечислить все отрасли, в которых трудился великий учёный. Но в первую очередь он был математиком.

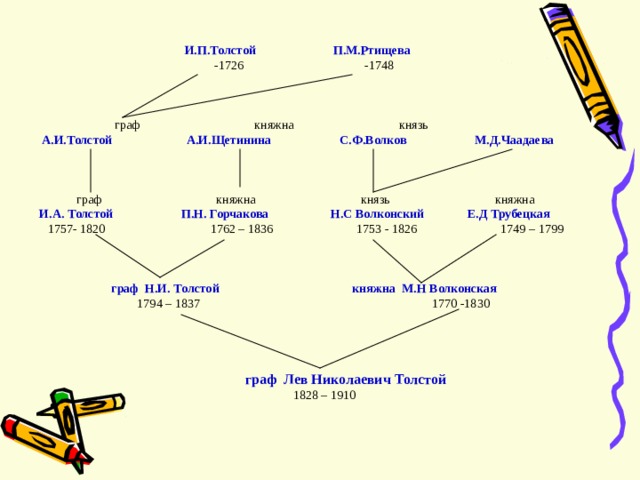
Использует графы и дворянство. На следующем слайде приведена часть генеалогического дерева знаменитого дворянского рода. Здесь его вершины – члены этого рода , а связывающие их отрезки — отношения родственности , ведущие от родителей к детям.

граф княжна князь

А.И.Толстой А.И.Щетинина С.Ф.Волков М.Д.Чаадаева

граф княжна князь княжна

И.А. Толстой П.Н. Горчакова Н.С Волконский Е.Д Трубецкая

1757- 1820 1762 – 1836 1753 — 1826 1749 – 1799

граф Н.И. Толстой княжна М.Н Волконская

1794 – 1837 1770 -1830

граф Лев Николаевич Толстой

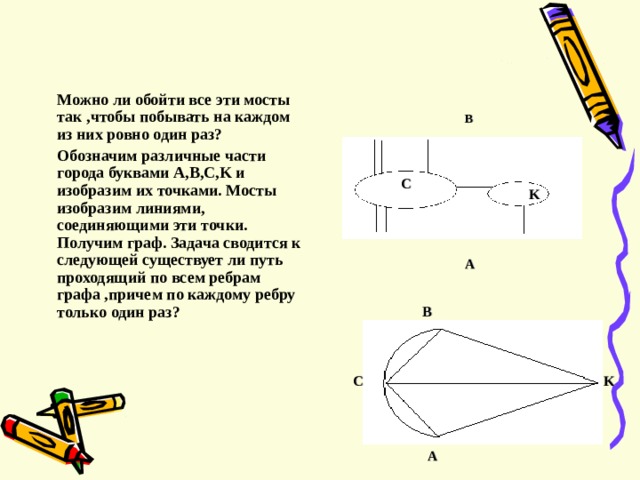
А началась теория графов с разбора широко известной теперь задачи о кенигсбергских мостах. Различные части города были соединены семью мостами , как показано на рисунке.

Можно ли обойти все эти мосты так , чтобы побывать на каждом из них ровно один раз ?

Обозначим различные части города буквами A,B,C,K и изобразим их точками. Мосты изобразим линиями , соединяющими эти точки. Получим граф. Задача сводится к следующей существует ли путь проходящий по всем ребрам графа , причем по каждому ребру только один раз ?

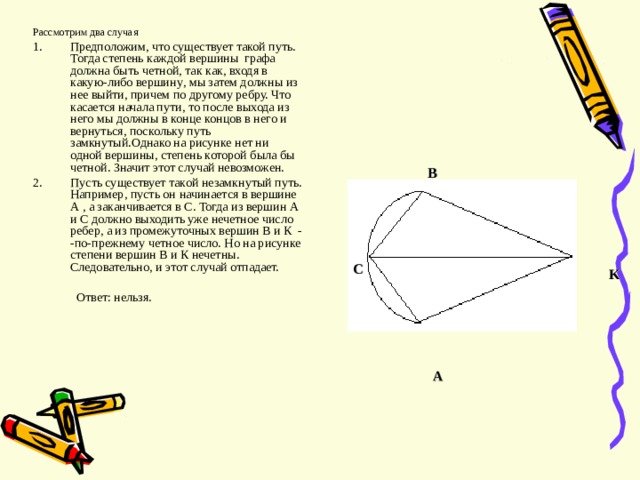
Рассмотрим два случая

• Предположим , что существует такой путь. Тогда степень каждой вершины графа должна быть четной , так как , входя в какую-либо вершину , мы затем должны из нее выйти , причем по другому ребру. Что касается начала пути , то после выхода из него мы должны в конце концов в него и вернуться , поскольку путь замкнутый.Однако на рисунке нет ни одной вершины , степень которой была бы четной. Значит этот случай невозможен.
• Пусть существует такой незамкнутый путь. Например , пусть он начинается в вершине А , а заканчивается в С. Тогда из вершин А и С должно выходить уже нечетное число ребер , а из промежуточных вершин В и К — -по-прежнему четное число. Но на рисунке степени вершин В и К нечетны. Следовательно , и этот случай отпадает.

Решая задачу о кенигсбергских мостах , Эйлер установил свойства графа , которые я рассмотрел в работе.

1.Если существует замкнутый путь, проходящий по всем ребрам графа, причем по каждому ребру только один раз, то степени всех вершин графа четные.

2. Если существует аналогичный незамкнутый путь, то степени начала и конца пути нечетные , а остальных вершин – четные.

Решение некоторых задач , представленных в работе я хочу показать.

Можно ли обвести карандашом , не отрывая его от бумаги и не проходя по одной линии дважды правильный пятиугольник с диагоналями ?

Ответ : можно , так как по Эйлеру степени начала и конца пути нечетные , а остальных вершин – четные.

Исходя из четности и нечетности вершин графа можно показать какие из букв русского алфавита можно нарисовать одним росчерком ?

Ответ : Б В Г З И Л М О П Р С Ф Ъ Я.

В первенстве класса по настольному теннису 6 участников: Андрей, Борис, Виктор, Галина, Дмитрий и Елена. Первенство проводят по круговой системе – каждый из участников играет с каждым из остальных один раз. К настоящему моменту некоторые игры уже проведены: Андрей сыграл с Борисом, Галиной, Еленой; Борис – с Андреем, Галиной; Виктор – с Галиной, Дмитрием, Еленой; Галина – с Андреем, Виктором и Борисом. Сколько игр проведено к настоящему моменту и сколько ещё осталось?

Построим граф (рис.)

Сыграно семь игр ( черный цвет ребер).

На рисунке граф имеет 8 ребер (красный цвет ребер) , следовательно , осталось провести 8 игр.

В школьном драматическом кружке решили ставить гоголевского “ Ревизора “ . И тут разгорелся жаркий спор. Все началось с Ляпкина- Тяпкина.

-Ляпкиным- Тяпкиным буду я ! — решительно заявил Дима.- С раннего детства я мечтал воплотить этот образ на сцене.

• Ну хорошо, согласен уступить эту роль, если мне дадут сыграть Хлестакова,- проявил великодушие Гена.
• А мне – Осипа, -не уступил ему в великодушии Дима.
• Хочу быть Земляникой или Городничим, -сказал Вова.
• Нет, Городничим буду я,- хором закричали Алик и Боря. – Или Хлестаковым,- добавили они одновременно.

Удастся ли распределить роли так, чтобы исполнители были довольны ?

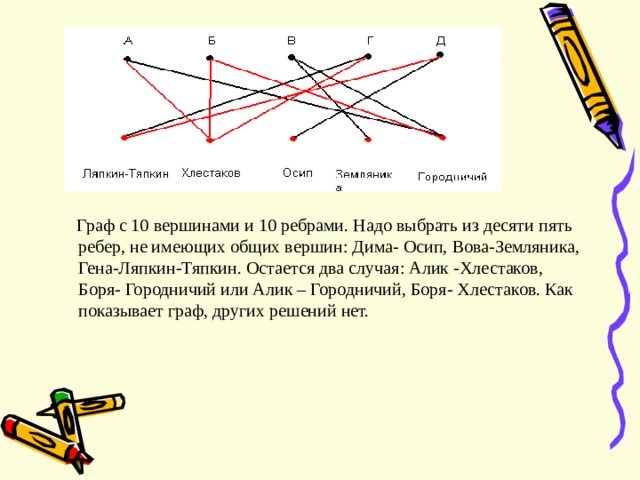
Построим граф для ситуации, описанной в задаче.

Граф с 10 вершинами и 10 ребрами. Надо выбрать из десяти пять ребер, не имеющих общих вершин : Дима- Осип, Вова-Земляника, Гена-Ляпкин-Тяпкин. Остается два случая : Алик -Хлестаков, Боря- Городничий или Алик – Городничий, Боря- Хлестаков. Как показывает граф, других решений нет.

В походе, который длился 12 дней, участвовали 9 человек. Каждый день дежурили 3 человека. При этом дежурные ссорились друг с другом, и никакие двое из них не хотели больше ни разу дежурить вместе. Тем не менее участники похода утверждают, что все 12 дней им удавалось назначать тройки дежурных с учетом этого требования. Могло ли так быть ?

Участники похода обозначены цифрами от 1 до 9, каждый столбец соответствует тройке дежурных.

Источник