Матричное представление графов



Для обработки на ЭВМ графы удобно представлять в виде матриц смежности и инциденций.
Матрица смежности – это квадратная матрица размерностью n x n, (где n – число вершин графа), однозначно представляющая его структуру.
A =
Матрица инциденций представляет собой прямоугольную матрицу размером n x m, где n – количество вершин графа, а m – количество дуг графа. Обозначается матрица инциденций B = =
Каждый элемент матрицы определяется следующим образом:
bij = 1, если хi является начальной вершиной дуги aj,
bij = –1, если хi является конечной вершиной дуги aj,
bij = 0, если хi не является концевой вершиной дуги aj или если aj является петлей.
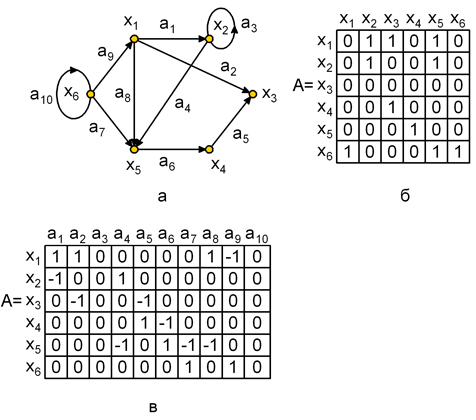
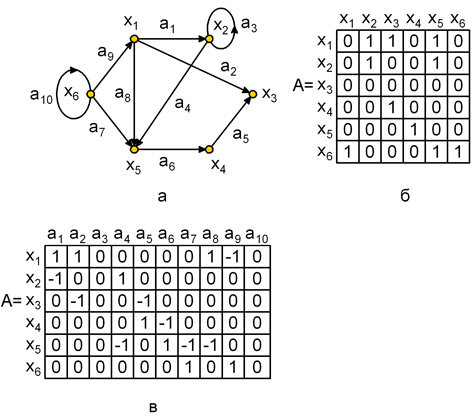
Рис.2. Орграф и его матричное представление: а – орграф; б – матрица смежности; в – матрица инциденций
На рис.2, а,б приведен граф и его матрица смежности, по которой можно найти характеристики вершин. Так сумма элементов i-ой строки матрицы дает полустепень исхода вершины хi, а сумма элементов i-го столбца дает полустепень захода вершины хi. По матрице смежности можно найти прямые и обратные отображения. Рассмотрим i-ю строку матрицы. Если элемент aij=1, то элемент графа хj входит в отображение Г(хi). Например, в 2-й строке матрицы А (рис.2,б) единицы стоят в 2-м и 5-м столбцах, следовательно, Г(х2) = < х2, х5>.
Для графа на рис.2,а матрица инциденций приведена на рис.4,в. Поскольку каждая дуга инцидентна двум различным вершинам, за исключением того случая, когда дуга образует петлю, то каждый столбец либо содержит один элемент равный 1 и один – равный – 1, либо все элементы столбца равны 0.
Для неориентированного графа, матрица инциденций определяется так же, за исключением того, что все элементы, равные –1, заменяются на 1.
Источник
Графы. Способы представления графа в программе
Граф в программировании представляет собой совокупность двух конечных множеств:
- множества вершин (точек, узлов);
- множества дуг (ребер), соединяющих вершины.
В качестве простейшего примера графа часто приводят систему дорог между городами, где города — это вершины, а дороги — ребра графа. Однако, вокруг нас есть множество и более обыденных примеров:
- электрическая схема является графом, в котором вершины — элементы схемы, а дуги — соединяющие провода;
- блок-схема алгоритма;
- система каталогов операционной системы является частным случаем графа — каталоги и папки задаются вершинами, а отношение вложенности — дугами.
Если направление ребер графа имеет значение (например при отражение отношения вложенности каталогов) — то граф называется ориентированным. Если направление не важно (например при соединении элементов электрической цепи) — граф является неориентированным. Кроме того, ребрам часто приписывается вес, граф в этом случае называется взвешенным — в системе дорог веса ребер могут отражать расстояния между городами.
В связи с этим возникает необходимость обработки графов компьютером, но для этого необходимо сначала каким-то удобным для обработки образом разместить его в памяти. Итак, граф ( G ) — это совокупность вершин ( V ), и дуг ( E ), в зависимости от того, как они задаются, выделяются следующие способы машинного представления графа:
- матрица смежности для графа из N вершин хранится в виду двумерного массива размером N x N . Вершины графа в этом случае задаются номерами (индексами строк и столбцов матрицы), а ячейка графа matrix[i, j] отражает наличие дуги между соответствующими вершинами. Например, при наличии дуги в ячейке может быть записана единица (или вес ребра i->j для взвешенного графа) , а при отсутствии — ноль;
- матрица инцидентности для графа из N вершин и M дуг хранится в виде двумерного массива размером N x M . Ячейка матрицы matrix[i, j] отражает инцидентность ребра j вершине i , т.е. тот факт, что это ребро выходит или входит в вершину i . Если ребро не связано с вершиной — в соответствующей ячейке матрицы записывается ноль, в противном случае единица (если граф ориентированный, то начало ребра можно отметить -1 , а конец 1 , если граф взвешенный — единица может быть заменена весом соответствующего ребра).
Матрица смежности графа:
| A | B | C | D | E | F | G | |
| A | 0 | 12 | 0 | 0 | 0 | 16 | 3 |
| B | 12 | 0 | 8 | 0 | 0 | 0 | 6 |
| C | 0 | 8 | 0 | 4 | 0 | 0 | 8 |
| D | 0 | 0 | 4 | 0 | 14 | 0 | 30 |
| E | 0 | 0 | 0 | 14 | 0 | 28 | 11 |
| F | 16 | 0 | 0 | 0 | 28 | 0 | 13 |
| G | 3 | 6 | 8 | 30 | 11 | 13 | 0 |
Матрица инцидентности графа:
| AB | BC | CD | DE | EF | FA | AG | BG | CG | DG | EG | FG | |
| A | 12 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 |
| B | 12 | 8 | 0 | 0 | 0 | 0 | 0 | 6 | 0 | 0 | 0 | 0 |
| C | 0 | 8 | 4 | 0 | 0 | 0 | 0 | 0 | 8 | 0 | 0 | 0 |
| D | 0 | 0 | 4 | 14 | 0 | 0 | 0 | 0 | 0 | 30 | 0 | 0 |
| E | 0 | 0 | 0 | 14 | 28 | 0 | 0 | 0 | 0 | 0 | 11 | 0 |
| F | 0 | 0 | 0 | 0 | 28 | 16 | 0 | 0 | 0 | 0 | 0 | 13 |
| G | 0 | 0 | 0 | 0 | 0 | 16 | 3 | 6 | 8 | 30 | 11 | 13 |
Работая с приведенными матрицами возможно, например, найти в графе кратчайшие пути между вершинами, построить минимальные остовы и т.д., однако, у них есть недостатки:
- избыточность. Зачастую в графах ребра существуют между небольшим (количеством вершин), поэтому в матрице смежности будет огромное количество нулей. В матрице инцидентности в каждом столбце может быть лишь два ненулевых значения (т.к. у дуги два конца). На хранение нулей тратится память, что может быть существенно при обработки больших графов;
- недостаточная расширяемость. В матрицу смежности можно без проблем добавлять новые дуги, но чтобы добавить вершину нужно создавать новую матрицу большего размера и копировать в нее данные из старой. Это работает очень медленно при больших матрицах. В матрице инцидентности такие проблемы возникнут как при добавлении дуг, так и при добавлении вершин.
В связи с этим, зачастую применяются списки смежности и инцидентности. Для каждой вершины при этом хранится список с номерами смежных вершин или инцидентных ребер. В качестве структуры данных при этом могут использоваться массивы, связные списки и даже хеш-массивы.
Списки смежности графа:
| A | B(12) | F(16) | G(3) | |||
| B | A(12) | C(8) | G(6) | |||
| C | B(8) | D(4) | G(8) | |||
| D | C(4) | E(14) | G(30) | |||
| E | D(14) | F(28) | G(11) | |||
| F | A(16) | E(28) | G(13) | |||
| G | A(3) | B(6) | C(8) | D(30) | E(11) | F(13) |
Списки смежности и инцидентности решают проблему расширяемости графа, т.к. новые узлы и дуги могут быть очень просто и эффективно добавлены во время выполнения программы, кроме того они более оптимальны по памяти, т.к. хранятся только данные о существующих дугах. Однако, такой способ представления графа менее эффективен по процессорному времени, т.к. для проверки существования дуги в худшем случае нужно будет перебрать все дуги, выходящие из некоторой вершины, но в матрице смежности было достаточно обратиться к элементу массива (асимптотическая сложность ухудшилась с O(1) до O(K) при использовании связных списков или O(log(K)) при использовании хеш-массивов). Важно, что K в этом случае — количество смежных вершин, для многих графов оно не будет очень большим (например, если граф представлял бы карту города, то скорее всего значение K для каждой вершины не превышало бы 4-6 ), в связи с этим, нужно очень внимательно выбирать структуру данных для хранения списков смежности/инцидентности.
Еще одним способом задания графа в программе может быть хранение указателей на смежные вершины/инцидентные дуги внутри каждого узла программы, при этом узел описывается в виде структуры, содержащей данные и эти указатели. Примерно так:
Сам граф в программе хранится в виде списка таких вершин.
Литература по теме:
- Анализ сложности алгоритмов. Примеры — поможет разобраться с оценкой сложности по памяти и процессорному времени (нужно чтобы уметь выбирать наиболее подходящую для своей задачи структуру данных);
- Макоха А. Н., Сахнюк П. А., Червяков Н. И. Дискретная математика: Учеб. пособие. — М. ФИЗМАТЛИТ, 2005 — 368 с.
- Дж. Макконелл Анализ алгоритмов. Активный обучающий подход. — 3-е дополненное издание. М: Техносфера, 2009. -416с.
Источник
Графы и способы их представления
Способы описания графов
Теоретико-множественное представление графов
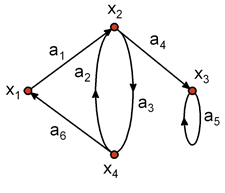
Граф описывается перечислением множества вершин и дуг. Примеры описания приведены для орграфов на рис. 1.3 и рис. 1.4.
где X =
Задание графов соответствием
Описание графов состоит в задании множества вершин Х и соответствия Г , которое показывает, как между собой связаны вершины.
Соответствием Г называется отображение множества Х в Х , а граф в этом случае обозначается парой G = (X, Г) .
Отображением вершины хi — Г(хi) является множество вершин, в которые существуют дуги из вершины хi , т. е. 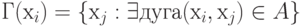
Так для орграфа на рис. 1.3 описание заданием множества вершин и соответствия выглядит следующим образом:
Для неориентированного или смешанного графов предполагается, что соответствие Г задает такой эквивалентный ориентированный граф , который получается из исходного графа заменой каждого неориентированного ребра двумя противоположно направленными дугами, соединяющими те же самые вершины. Например, для графа на рис. 1.2,б Г(х2) = < х1, х3, х5 >, Г(х4) =< х3, х5> и т. д.
Матричное представление графов
Для обработки на ЭВМ графы удобно представлять в виде матриц смежности и инциденций .
Матрица смежности – это квадратная матрица размерностью n x n , (где n – число вершин графа ), однозначно представляющая его структуру.
A =
aij = 1 , если 
Если элемент на диагонали (i=j) равен единице, значит, вершина i имеет петлю.
Матрица инциденций представляет собой прямоугольную матрицу размером n x m , где n – количество вершин графа , а m – количество дуг графа . Обозначается матрица инциденций B =
Каждый элемент матрицы определяется следующим образом:
bij = 1 , если хi является начальной вершиной дуги aj ,
bij = –1 , если хi является конечной вершиной дуги aj ,
bij = 0 , если хi не является концевой вершиной дуги aj или если aj является петлей.
Таким образом, нулевой столбец j в матрице инциденций свидетельствует о том, что дуга aj яляется петлей.
На рис. 1.5, а,б приведен граф и его матрица смежности , по которой можно найти характеристики вершин. Так сумма элементов i -ой строки матрицы дает полустепень исхода вершины хi , а сумма элементов i -го столбца дает полустепень захода вершины хi . По матрице смежности можно найти прямые и обратные отображения. Рассмотрим i -ю строку матрицы. Если элемент aij=1 , то элемент графа хj входит в отображение Г(хi) . Например, во 2-й строке матрицы А ( рис. 1.5,б) единицы стоят в 2-м и 5-м столбцах, следовательно, Г(х2) = < х2, х5> .
Для графа на рис. 1.5,а матрица инциденций приведена на рис. 1.5,в. Поскольку каждая дуга инцидентна двум различным вершинам, за исключением того случая, когда дуга образует петлю, то каждый столбец либо содержит один элемент равный 1 и один – равный – 1, либо все элементы столбца равны 0.
Для неориентированного графа , матрица инциденций определяется так же, за исключением того, что все элементы, равные –1, заменяются на 1.
Источник