Способы представления графов дерево

8 . Нелинейные структуры данных. Деревья и графы

Рассмотренные ранее структуры данных (массивы, массивы указателей и списки) имеют линейную структуру, единственный порядок обхода, который и определяет порядок следования (перечисления, логической нумерации) элементов. Деревья и графы, наоборот, представляют собой структуры, которые не допускают подобной «линеаризации»: их невозможно «вытянуть в линию» и для их изображения необходима плоскость. С точки зрения организации данных это дает разнообразие вариантов размещения одного и того же набора данных, а также различные варианты обхода одной и той же структуры.

8 .1. Деревья и рекурсивные алгоритмы

Определение дерева. Дерево и рекурсия

void ScanTree ( текущая вершина)<

if ( текущая вершина ==NULL) return;

for ( перебор потомков) ScanTree ( i -ый потомок)

Когда речь идет о древовидных структурах, следует отличать их абстрактное определение от конкретного способа их реализации в памяти. Последнее зависит также от вида алгоритмов, работающих с деревом:

— если используется рекурсивный или циклический алгоритм, начинающий работать с корневой вершины дерева, то необходимы только прямые ссылки от предка к потомкам;

— если алгоритм предполагает навигацию по дереву во всех направлениях, как вверх, так и вниз по дереву (например, в древовидной системе каталогов), то предполагается наличие как прямых, так и обратных ссылок от потомков к предкам (в системе каталогов – ссылка на родительский каталог);

— возможны алгоритмы, которые работают с деревом, начиная с терминальных вершин. Тогда кроме ссылок от потомков к предкам необходима еще структура данных, объединяющая терминальные вершины (например, массив указателей).

Способы представления деревьев

До сих пор мы говорили о деревьях абстрактно, как о логической структуре. А теперь спустимся на грешную землю и обсудим варианты его физического размещения. Составными частями физического представления дерева могут быть массивы, списки, массивы указателей. Начнем с самого простого.

void scan_m(mtree A[], int n, int k, int level)< // k – индекс предка

printf(«l=%d node=%d s=%s\n»,level,k,A[k].s);

for ( int i =0; i n ; i ++) // Цикл выбора потомков вершины

if (A[i].parent==k) scan_m(A,n,i,level+1);>

void scan _2( int A[], int n, int k,int level)< // k – индекс текущей вершины

printf(«l=%d node=%d val=%d\n»,level,k,A[k]);

// 0 1 2 3 4 5 6 7 8 9

Получается быстро, а главное, без дополнительной информации, индекс массива однозначно определяет положение вершины. Но за это приходится расплачиваться. Каждый следующий уровень требует удвоения размерности массива, вне зависимости от того, сколько вершин этого уровня используются. Поэтому основное требование – сбалансированность. Если есть хотя бы одна ветвь, сильно отличающаяся по длине, то эффективность использования памяти резко снижается. Если же дерево вырождается в список, то размерность массива растет экспоненциально W=2 N .

Каждая вершина содержит два указателя – на «старшего сына» – заголовок списка следующего уровня, и на «следующего брата» — ссылка в списке вершин текущего уровня.

// Представление дерева в виде разветвляющегося списка

ltree *son,*bro; // Указатели на старшего сына

>; // и младшего брата

ltree A=<"aa",NULL,NULL>, // Последняя в списке

C=<"cc",NULL,&B>, // Список потомков — концевых вершин A,B,C D =<" dd ", NULL , NULL >,

F=<"ff",&D,&E>, // Список потомков G — вершин F,E

Читайте также:  Автомобильная мастика способ применения

void scan_l(ltree *p, int level)<

if (p==NULL) return;

for (ltree *q=p->son;q!=NULL;q=q->bro)

int n ; // Количество потомков в МУ

void scan(tree *p, int level)<

if (p==NULL) return;

Эффективность алгоритмов, работающих с деревьями

Можно провести аналогии между парой «деревья — рекурсивные алгоритмы» и «пространство-время». При работе рекурсивной программы происходит развертке дерева вызовов функции во времени, а дерево, как структура данных, выглядит как отображенный в памяти результат выполнения рекурсивного алгоритма. Именно поэтому к деревьям применимы выводы относительно эффективности рекурсивных алгоритмов:

— полный рекурсивный обход дерева имеет линейную трудоемкость;

— явный результат рекурсивной функции предполагает его накопление в процессе выполнения цепочки возвратов из рекурсивной функции (т.е. накопление результат идет в обратном направлении – от потомков к предку). При этом каждая вершина, получая результаты от потомков, вносит собственную «ложку дегтя», т.е. объединяет результаты поддеревьев с собственным;

— возможно использование формального параметра – ссылки, которая передается по цепочке рекурсивных вызовов. В этом случае все рекурсивные вызовы ссылаются на общую переменную, которая играет роль глобальных данных, используемых для накопления результата.

N = 1 + m + m 2 + m 3 + … + m L m L , L

В самом худшем случае при наличии только одного потомка в каждой вершине дерево вырождается в список, в этом случае длина ветви равна количеству вершин без 1.

для вырожденного в список дерева – линейной. Здесь возникают две проблемы. Во-первых, поддержка сбалансированности дерева. Для нее имеется два решения:

— использование алгоритмов, сохраняющих сбалансированность дерева, которые являются значительно более сложными, чем обычно, поскольку используют различные топологические преобразования групп смежных вершин дерева (причем рекурсивно);

— периодическое выравнивание (балансировка) дерева, возможно с использованием дополнительной структуры данных. Данное решение позволяет использовать простые алгоритмы работы с деревом, но требует слежения за его сбалансированностью (заметим, что это могут делать те же самые алгоритмы, например, определяя длину ветви при поиске заданного значения). Процедура балансировки может быть достаточно трудоемкой, но вызываемой сравнительно редко.

На житейском уровне эту альтернативу можно сформулировать как «идеальный порядок или периодическая генеральная уборка». Аналогичная ситуация возникает в любых системах динамического распределения и утилизации ресурсов: в системе динамического распределения памяти (2.6), при планировании двоичного файла (9.2), в системе управления файлами операционной системы, где она имеет похожие решения.

Вторая проблема упирается в основания, которые имеет алгоритм для однозначного выбора единственного потомка в каждой вершине (художественная аналогия — «рыцарь на распутье»). Здесь опять же возможны два подхода:

— наличие в вершине дополнительной (избыточной) информации, позволяющей сделать такой выбор «здесь и сейчас»;

— наличие определенного порядка размещения данных в дереве.

Источник

Графы и деревья

Способы представления деревьев

Поскольку любое дерево является графом , то его можно задавать любым из способов, перечисленных в п. «Способы представления графов «. Однако существуют и специальные способы представления, предназначенные только для деревьев . Мы рассмотрим только два наиболее распространенных частных случая.

Представление корневого дерева

Этот способ подходит только для тех корневых деревьев , у которых точно известно максимальное количество потомков для любой вершины .

Разумеется, в общем случае значение переменной S (количество потомков ) может достигать N-1 ( N — количество всех вершин в дереве ). Однако ясно, что в такой ситуации особого смысла в динамической древесной структуре нет: экономии памяти не получается. Гораздо лучше, если у всех вершин примерно одинаковое и заранее известное количество потомков .

Представление бинарного дерева

Разновидностью описанного выше частного случая является бинарное корневое дерево : каждая его вершина имеет не более двух потомков :

Примеры использования деревьев

Здесь мы ограничимся только примерами использования бинарных корневых деревьев : именно такой вид графа чаще всего применяется в программировании.

Дерево двоичного поиска

Дерево двоичного поиска для множества чисел S — это размеченное бинарное дерево , каждой вершине которого сопоставлено число из множества S , причем все пометки удовлетворяют следующим условиям:

1. существует ровно одна вершина , помеченная любым числом из множества S ;
2. все пометки левого поддерева строго меньше, чем пометка текущей вершины ;
3. все пометки правого поддерева строго больше, чем пометка текущей вершины .

Если выражаться простым языком, то структура дерева двоичного поиска подчиняется простому правилу: «если больше — направо, если меньше — налево».

Например, для набора чисел 7 , 3 , 5 , 2 , 8 , 1 , 6 , 10 , 9 , 4 , 11 получится такое дерево (см. рис. 11.14).

Для того чтобы правильно учесть повторения чисел, можно ввести дополнительное поле, которое будет хранить количество вхождений для каждого числа.

Более подробно процессы построения и анализа дерева бинарного поиска будут изложены в следующей лекции, посвященной алгоритмам, использующим деревья и графы .

Дерево частотного словаря

Дерево частотного словаря — это результат построения дерева двоичного поиска не для чисел, а для слов некоторого текста. Генерирование дерева частотного словаря полезно при подсчете количества вхождений каждого слова в некоторый текст.

Приведем описание структуры этого дерева :

Дерево синтаксического анализа

Дерево синтаксического анализа арифметического выражения — это бинарное дерево , листьями которого служат операнды, а остальными вершинами — операции, причем уровень вершины соответствует приоритету выполнения операции: чем ближе к листьям , тем приоритет выше.

Например, на рис. 11.15 изображено дерево синтаксического анализа для выражения ((a / (b + c)) + (x * (y — z))) .

Деревья синтаксического разбора строятся компиляторами во время синтаксического анализа программ. Помимо арифметических выражений, которые являются простейшим случаем, аналогичные, но более сложные деревья строятся для всех грамматических конструкций компилируемой программы.

Источник

Графы и деревья

Чуть-чуть истории

Теория графов — довольно молодая наука (по сравнению, скажем, с геометрией ). В 1736 году Санкт-Петербургская академия наук опубликовала труд Леонарда Эйлера, где рассматривалась задача о кенигсбергских 1 Ныне — Калининград. мостах («Можно ли, пройдя все городские мосты ровно по одному разу, вернуться в исходную точку?»). Это была первая работа по будущей теории графов .

Особенно приятно то, что в данном случае Россия — родина пусть и не новой породы слонов, но зато нового научного направления!

Графы: определения и примеры

Итак, перейдем к изложению некоторых понятий современной теории графов .

Неориентированные графы

Граф — это двойка , где V — непустое множество вершин , а Е — множество ребер, соединяющих эти вершины попарно 2 Более корректно: Е — это множество двухэлементных подмножеств (неупорядоченных пар) множества V , называемых ребрами . Из такого определения видно, что любые две вершины могут быть соединены не более чем одним ребром . . Две вершины , связанные между собой ребром , равноправны, и именно поэтому такие графы называются неориентированными: нет никакой разницы между «началом» и «концом» ребра .

Таблица 11.1. Примеры неориентированных графов

Граф	Вершины	Ребра
Семья	Люди	Родственные связи
Город	Перекрестки	Улицы
Сеть	Компьютеры	Кабели
Домино	Костяшки	Возможность
Дом	Квартиры	Соседство
Лабиринт	Развилки и тупики	Переходы
Метро	Станции	Пересадки
Листок в клеточку	Клеточки	Наличие общей границы

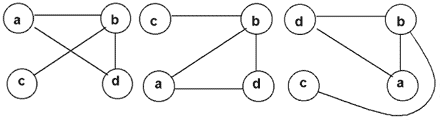
Говоря простым языком, граф — это множество точек (для удобства изображения — на плоскости) и попарно соединяющих их линий (не обязательно прямых). В графе важен только факт наличия связи между двумя вершинами . От способа изображения этой связи структура графа не зависит.

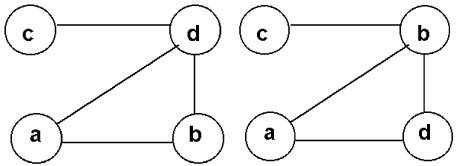
Например, три графа на рис. 11.1 совпадают, а два графа на рис. 11.2 — различны.

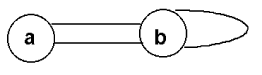
Из приведенного выше определения вытекает, что в графах не бывает петель — ребер, соединяющих некоторую вершину саму с собой (см. рис. 11.3). Кроме того, в классическом графе не бывает двух различных ребер, соединяющих одну и ту же пару вершин .

Ребро е и вершина v называются инцидентными друг другу, если вершина v является одним из концов ребра е .

Любому ребру инцидентно ровно две вершины , а вот вершине может быть инцидентно произвольное количество ребер, это количество и определяет степень вершины . Изолированная вершина вообще не имеет инцидентных ей ребер (ее степень равна 0 ).

Две вершины называются смежными, если они являются разными концами одного ребра (иными словами, эти вершины инцидентны одному ребру ). Аналогично, два ребра называются смежными, если они инцидентны одной вершине .

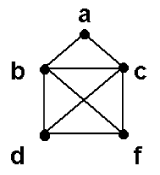
Путь в графе — это последовательность вершин (без повторений), в которой любые две соседние вершины смежны. Например, в графе , изображенном на рис. 11.1, есть два различных пути из вершины a в вершину с : adbc и abc .

Вершина v достижима из вершины u , если существует путь , начинающийся в u и заканчивающийся в v .

Граф называется связным , если все его вершины взаимно достижимы .

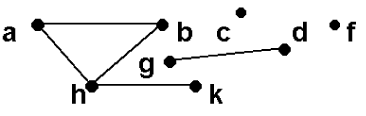
Компонента связности — это максимальный связный подграф . В общем случае граф может состоять из произвольного количества компонент связности . Заметим, что любая изолированная вершина является отдельной компонентой связности . На рис. 11.4 изображен граф , состоящий из четырех компонент связности : [abhk] , [gd] , [c] и [f] .

Длина пути — количество ребер, из которых этот путь состоит. Например, длина уже упомянутых путей adbc и abc (см. рис. 11.1) — 3 и 2 соответственно.

Говорят, что вершина v принадлежит k -му уровню относительно вершины u , если существует путь из u в v длиной ровно k ребер. Одна и та же вершина может относиться к разным уровням . Например, в графе , изображенном на рис. 11.1, относительно вершины a существует 4 уровня :

• 0) a ;
• 1) b , d ;
• 2) b , d , c ( пути adb , abd , abc );
• 3) c ( путь adbc ).

Расстояние между вершинами u и v — это длина кратчайшего пути от u до v . Из этого определения видно, что расстояние между вершинами a и c в графе на рис. 11.1 равно 2 .

Цикл — это замкнутый путь . Все вершины в цикле , кроме первой и последней, должны быть различны. Например, циклом является путь abda в графе на рис. 11.1.

Эйлеров граф — это граф , в котором существует путь или цикл , содержащий все ребра графа ( вершины могут повторяться). Именно такие графы положительно решают упомянутую в начале лекции задачу о кенигсбергских мостах. Например, граф на рис. 11.5 является Эйлеровым: искомым путем в нем будет dbacfbcdf .

Гамильтонов граф — это граф , в котором существует путь или цикл (без повторений), содержащий все вершины графа (см. рис. 11.5; искомый цикл : abdfca ).

Источник