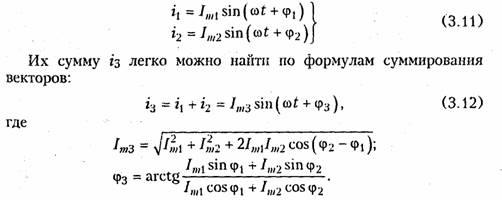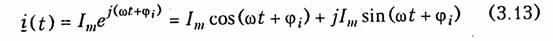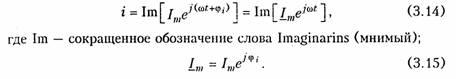Способы представления гармонического колебания

Методы представления колебаний

Существуют различные методы описания гармонических колебаний. Приведём некоторые из них.

1. Аналитический метод

Задаётся уравнение колебаний гармонического осциллятора

по которому и определяется смещение его от положения равновесия в любой момент времени.

2. Графический метод

Рис.5.3

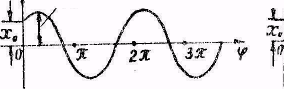
Строятся график гармонического колебания (рис.5.3) х=Аsin(ωt+φ₀). По оси абсцисс (ОХ) откладывается время t или фаза колебаний ωt+φ₀, по оси ординат (ОУ) – смещение х от положения равновесия.

3. Метод векторной диаграммы

Рис.5.4

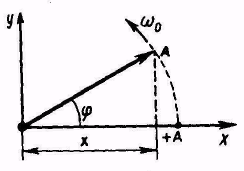
Этот метод состоит в следующем. Гармоническое колебание может быть задано с помощью вектора, длина которого равна амплитуде А колебания, а направление образует с осью х угол, равный начальной фазе колебания (рис. 5.4). Если привести этот вектор во вращение с угловой скоростью ω₀, то проекция конца вектора на ось х будет перемещаться в пределах от +А до -А, а колеблющаяся величина будет изменяться со временем по закону

x = Asin(ω₀t+φ₀), совершая гармоническое колебание.

§ 5.2.2 Скорость и ускорение колеблющейся точки

Чтобы найти скорость материальной точки при гармоническом колебании, возьмем производную от смещения колеблющейся точки x = Asin(ω₀t+φ₀) по времени:

(5.4)

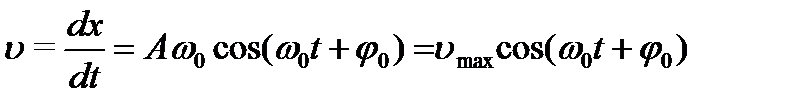
где υ_max = Аω₀ — максимальная скорость (амплитуда скорости).

На основании тригонометрических формул преобразуем (4.18):

(5.5)

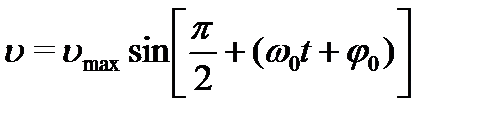
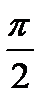
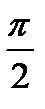
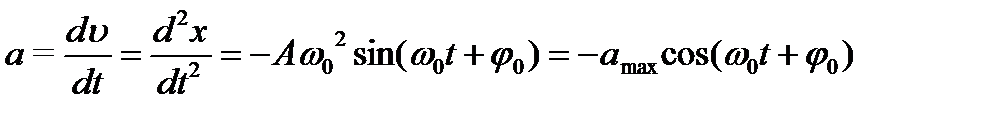
Сравнивая выражения для смещения и скорости замечаем, что фаза скорости на больше фазы смещения, т.е. скорость опережает по фазе смещение на Продифференцировав (5.4), найдем ускорение:

(5.6)

где а_max = А ω₀ 2 — максимальное ускорение (амплитуда ускорения).

Вместо (5.5) запишем

Из сравнения (5.6) и (5.3) следует, что фазы ускорения и смещения различаются на π, т. е. эти величины изменяются в противофазе. Это значит, что при положительном максимальном смещении ускорение максимально, но отрицательно. На рисунке показаны графические зависимости смещения, скорости и ускорения от времени (рис.6.6, а) и их векторные диаграммы (рис.5.6, б) .

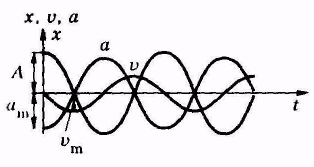
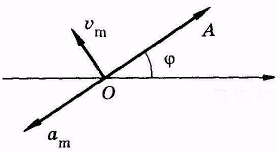
Рис.5.6

б )

а )

§ 5.2.3 Кинетическая и потенциальная энергии колебательного движения

Колеблющееся тело обладает как кинетической, так и потенциальной энергией, которые последовательно переходят друг в друга при колебаниях осциллятора. Полная энергия осциллятора равна сумме кинетической и потенциальной энергии:

Кинетическая энергия тела, колеблющегося по гармоническому закону, вычисляют по формуле:

(5.9)

с учётом mω 2 = k

Потенциальную энергию колебательного движения найдём, исходя из формулы для потенциальной энергии упругой деформации:

(5.10)

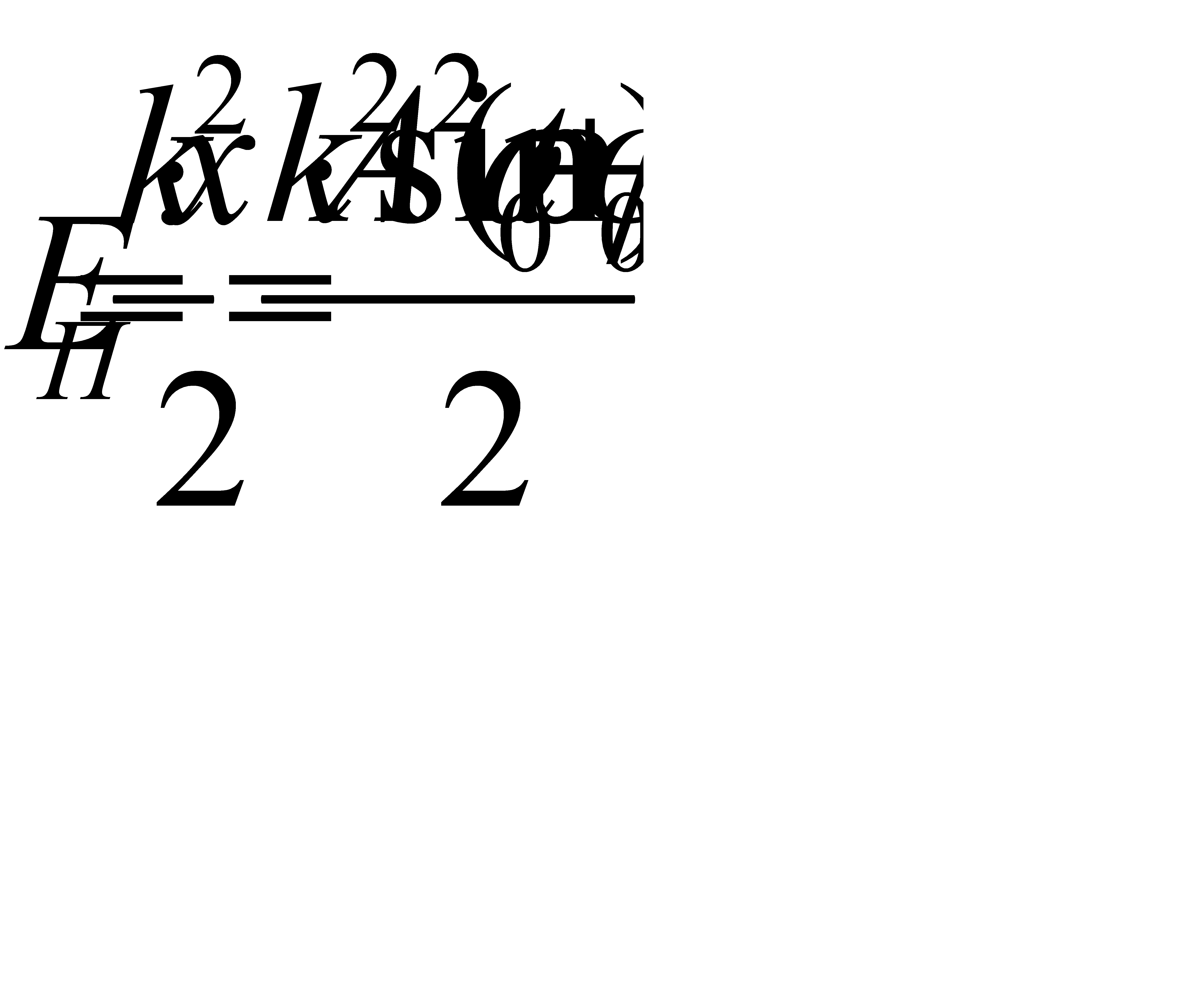
Складывая кинетическую и потенциальную энергию, получим полную механическую энергию материальной точки, колеблющейся по гармоническому закону:

(5.11)

Полученное выражение показывает, что энергия колеблющегося тела от времени не зависит, т.е. с течением времени остаётся величиной постоянной, а зависит только от квадрата амплитуды и частоты.

При отсутствии сил трения полная механическая энергия системы не изменяется:

(5.12)

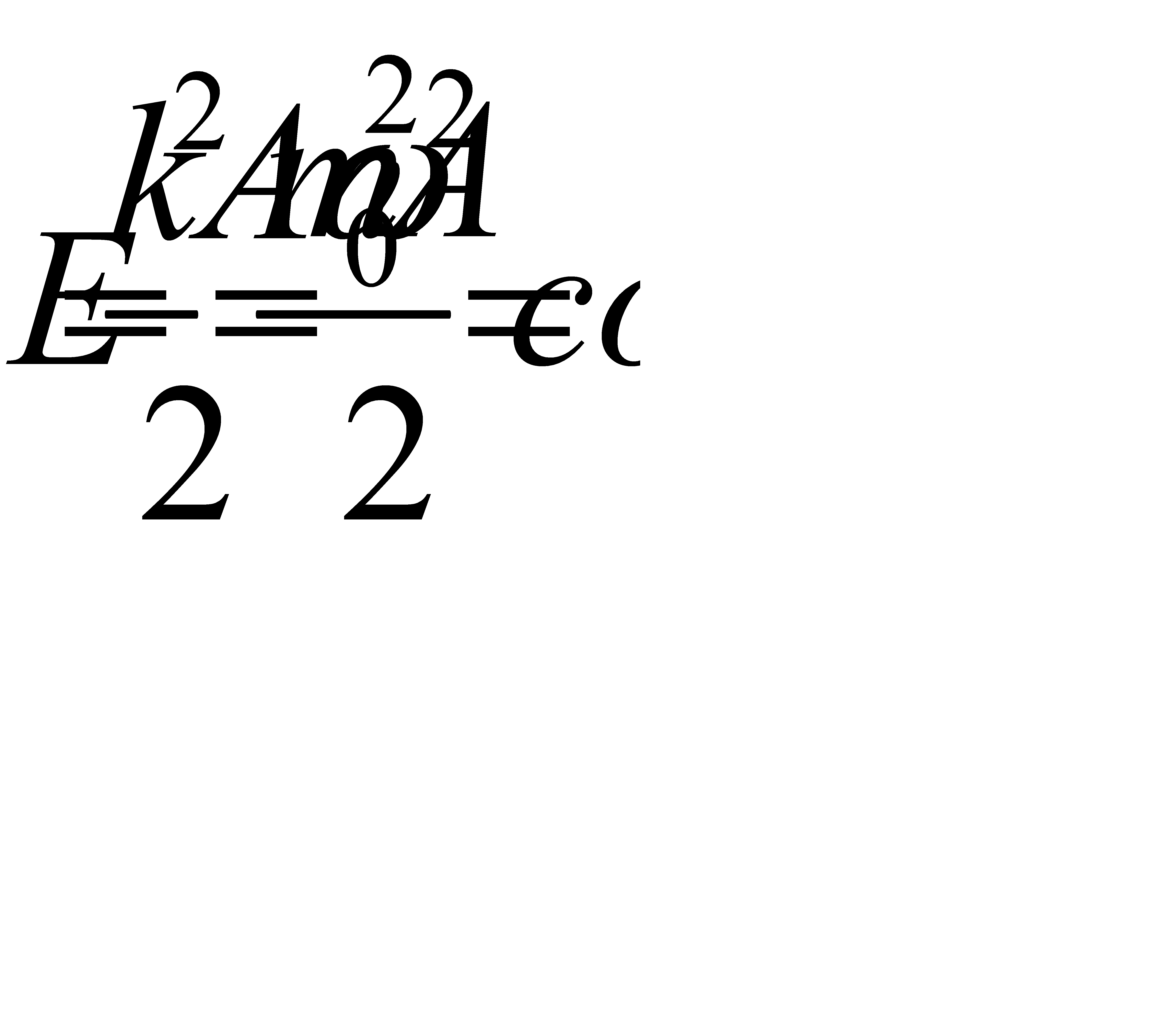
Графически зависимости кинетической, потенциальной и полной механической энергий колеблющейся системы от времени показаны на рис. 5.7, а.

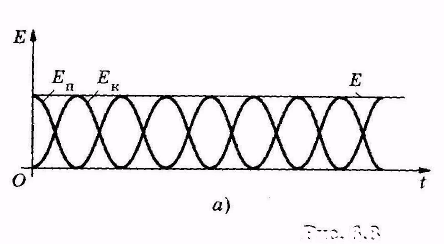
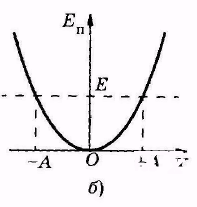
Рис.5.7

Потенциальная яма (ограниченная область пространства, в которой потенциальная энергия меньше, чем в не её), соответствующая гармоническому колебанию, изображена на рис. 5.7, б. Она определяется зависимостью 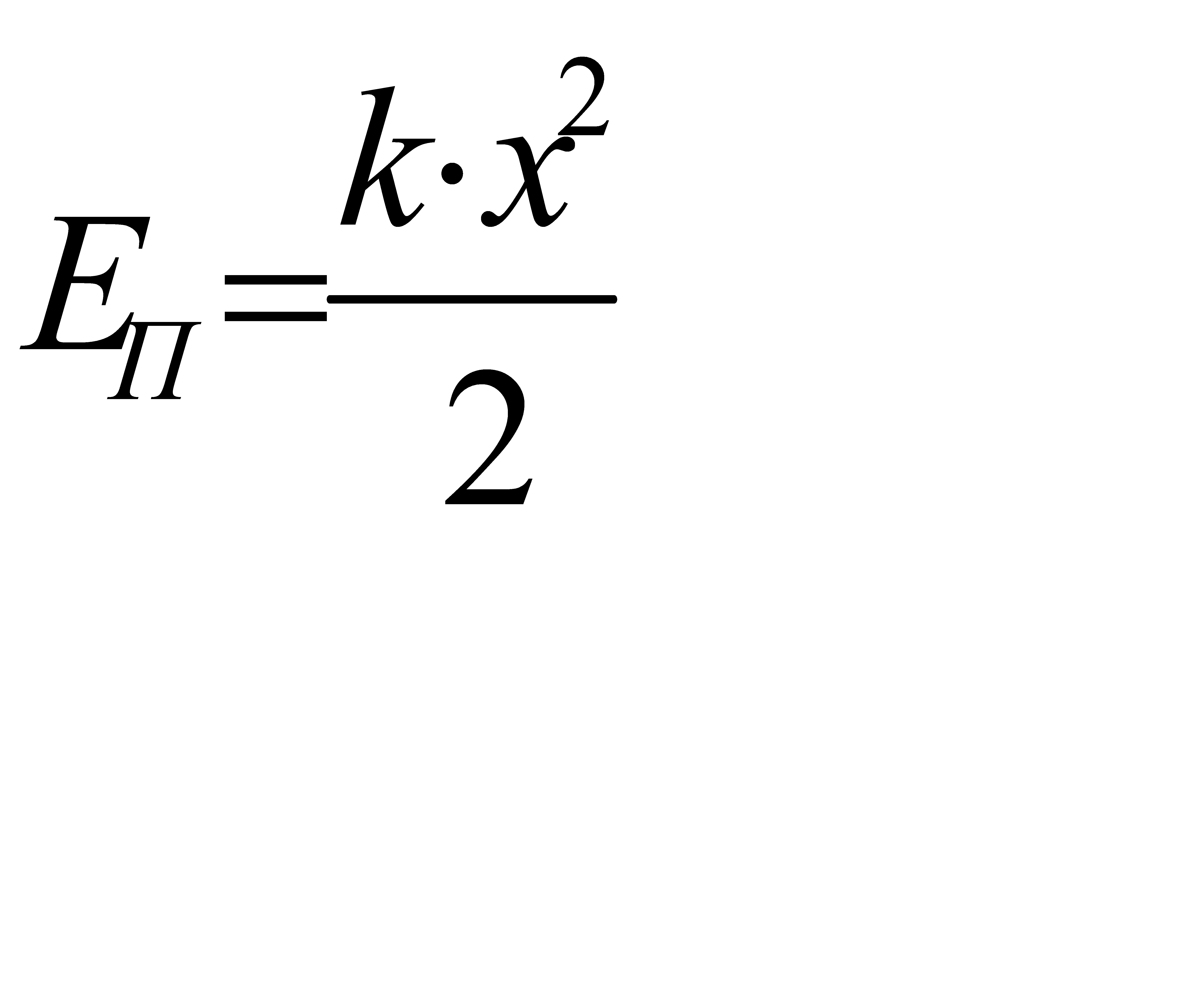. Отложив на оси ординат полную механическую энергию Е, по графику определяют интервал координат (-А, +А), за пределы которого частица, обладающая такой энергией, выйти не может.

§6.2 Затухающие колебания

До сих пор мы рассматривали свободные колебания материальной точки без учёта сопротивления среды, в которой происходят эти колебания.

В реальных условиях на колеблющееся тело всегда действуют силы сопротивления (трения), в результате чего амплитуда с течением времени уменьшается и колебания становятся затухающими.

Рис.5.8

Пусть маятник колеблется в вязкой среде (рис.). В этом случае на осциллятор кроме возвращающей силы F_упр = -kx будет действовать ещё одна сила – сила сопротивления среды F_с. При малых колебаниях скорость движения осциллятора мала, поэтому сила сопротивления пропорциональна скорости и направлена в противоположную сторону:

(5.13)

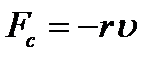
где r – коэффициент сопротивления среды, зависящий от плотности среды и геометрических размеров осциллятора; υ — относительная скорость движения осциллятора и среды.

Уравнение затухающих колебаний записывается в виде:

Выражение А=±А₀ е -δ t , есть переменная во времени амплитуда колебания; А₀— амплитуда в момент t = 0; ω -частота затухающих колебаний; φ₀-начальная фаза колебаний.

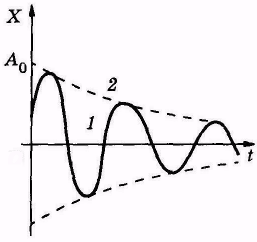
Рис. 6.9

График этой функции изображён на рисунке (кривая 1)пунктирнаялиния 2изображает ход убывания амплитуды. Материальная точка колеблется по закону синуса, но амплитуда колебания с течением времени уменьшается по экспоненте. Затухания происходят тем быстрее, чем больше δ, т.е. с увеличением внутреннего трения среды и уменьшением массы осциллятора.

Наглядной характеристикой затухания является отношение двух амплитуд, отличающихся по времени на период Т. Это соотношение называется декрементом затухания

(5.15)

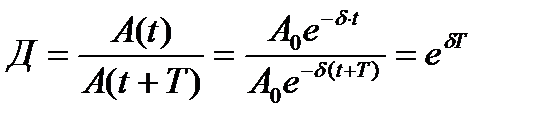
Прологарифмируем это выражение:

(5.16)

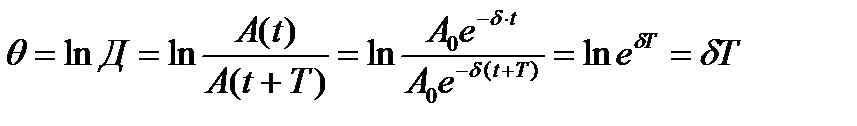
Значение θ=δТ называется логарифмическим декрементом затухания.

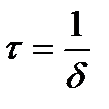
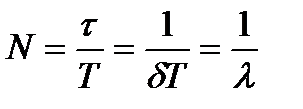
Время в течении которого амплитуда убывает в е раз, называется временем жизни колеблющейся точки. За время жизни τ система успевает совершить N колебаний.

(5.17)

Следовательно, логарифмический декремент затухания есть величина, обратная числу колебаний осциллятора за время его жизни.

Период затухающих колебаний зависит от коэффициента сопротивления rи определяется формулой:

(5.18)

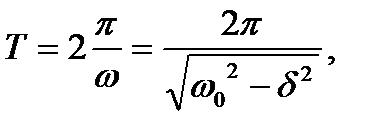
§6.3 Вынужденные колебания. Резонанс

Для того, чтобы колебания осциллятора были незатухающими, надо компенсировать потери энергии на преодоления сопротивления среды. Это можно сделать следующим способом. Пусть пружинный маятник с железным грузом находится в поле тяжести электромагнита, по обмотке которого проходит переменный ток:

Магнитная сила, действующая на маятник, меняется по тому же закону F_в=F₀sinωt. Эта периодически изменяющаяся внешняя сила, действующая на осциллятор, называется вынуждающей силой.

Колебания, возникающие под действием внешней периодически изменяющейся силы, называют вынужденными колебаниями.

Рис.6.11

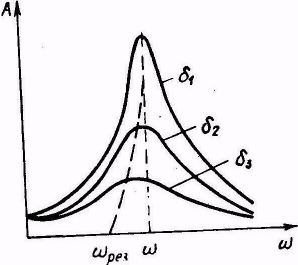
Зависимость амплитуды колебаний от частоты вынуждающей силы при различных δ приведены на рис. При ω → 0 амплитуда стремится к предельной величине, равной смещению осциллятора под действием постоянной силы F₀:

(6.42)

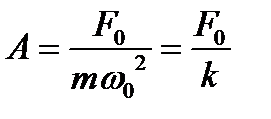
Когда частота вынуждающей силы приближается к частоте собственных колебаний осциллятора, амплитуда колебаний возрастает и при некоторой частоте достигает максимального значения. Это явление называется резонансом.

Существуют и такие колебательные системы, которые сами регулируют периодическое восполнение растраченной энергии и поэтому могут колебаться длительное время. Незатухающие колебания, существующие в какой-либо системе при отсутствии переменного внешнего воздействия, называются автоколебаниями, а сами системы — автоколебательными. Амплитуда и частота автоколебаний зависят от свойств самой автоколебательной системы, в отличие от вынужденных колебаний они не определяются внешними воздействиями.

Классическим примером механической автоколебательной системы являются часы, в которых маятник (или баланс) является колебательной системой, пружина (или поднятая гиря) — источником энергии, а анкер — регулятором поступления энергии от источника в колебательную систему. Некоторые биологические системы (сердце, легкие) являются автоколебательными.

Дата добавления: 2015-12-08 ; просмотров: 1883 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

2.2. Способы представления гармонических колебаний

Гармонические колебания можно представить различными спо­собами: функциями времени (временные диаграммы) (см. рис. 3.1); вращающимися векторами (векторные диаграммы); ком­плексными числами; амплитудными и фазовыми спектрами. Тот или иной способ представления применяется в зависимости от характера решаемых задач.

Временное представление гармонических колебаний наглядно, однако его использование в задачах анализа цепей затруднительно, так как требует проведения громоздких тригонометрических пре­образований. Более удобно векторное представление гармони­ческих колебаний, при котором каждому колебанию ставится в со­ответствие вращающийся вектор определенной длины с заданной начальной фазой. В качестве примера на рис. 3.3 показано вектор­ное представление двух колебаний токов i ₁ и i₂:

Величина φ= φ₂ —φ₁ называется фазовым сдвигом между колебаниями i ₁ и i₂. Он определяется только началь­ными фазами φ₂ и φ₁ и не зависит от начала отсчета времени. Нетрудно ви­деть, что суммирование (наложение) любого числа гармонических колебаний с частотой со приводит к гармоническому колебанию той же частоты со.

Совокупность векторов, изображающих гармонические колебания в электрической цепи, называют векторной диаграммой. Векторные диаграммы можно строить как для амплитудных, так и для действующих значений токов и на­пряжений.

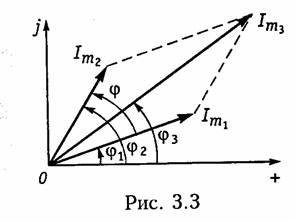
Наиболее распространенными являются представления гармо­нических колебаний с помощью комплексных чисел. Эти представ­ления лежат в основе символического метода расчета электриче­ских цепей — метода комплексных амплитуд. Представим ток i, определяемый формулой (3.6), на комплексной плоскости. Для этого изобразим вектор I_т на комплексной плоскости с учетом на­чальной фазы φ_i (рис. 3.4, а). Знаком «+» обозначено положи­тельное направление вещественной оси, а j = √-1 — положитель­ное направление мнимой оси. Будем вращать этот вектор в поло­жительном направлении (против часовой стрелки) с угловой час­тотой со. Тогда в любой момент времени положение вращающегося вектора определится комплексной величиной (комплексным гармо­ническим колебанием):

Первая часть слагаемого (3.13) отражает проекцию вращающего­ся вектора на вещественную ось, а вторая часть — на мнимую ось. Сравнив второе слагаемое в (3.13) с (3.6), приходим к вы­воду: синусоидальный ток i на комплексной плоскости представляется

в форме проекции иа мнимую ось вращающегося вектора (3.13)

Величина I_т носит название комплексной амплитуды тока.

Важным свойством комплексной амплитуды является то, что она полностью определяет гармоническое колебание заданной час­тоты ω, так как содержит информацию об его амплитуде и на­чальной фазе.

Если гармоническое колебание задается в форме косинусоиды, например

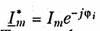
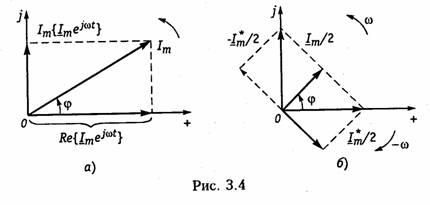
где -сопряжение комплексная амплитуда тока.

Таким образом, ток i из (3.6) согласно (3.19) можно предста­вить как геометрическую разность векторов 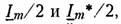вращаю­щихся в противоположных направлениях с угловой частотой со, а ток из (3.16) — как геометрическую сумму этих векторов (рис. 3.4, б). В первом случае i располагается на мнимой, а во втором случае — на действительной осях. Комплексную амплитуду синусоидальной функции заданной частоты можно рассматривать как преобразование временной функции в частотную область.

Спектральное (частотное) представление гармонических коле­баний состоит в задании амплитудного и фазового спектров коле­бания (рис. 3.5). Более подробно спектральное представление и методы анализа цепей, основанные на этом, представлении, рас­смотрены в гл. 5, 9.

Источник