Способы представления гармонических колебаний

Методы представления колебаний

Существуют различные методы описания гармонических колебаний. Приведём некоторые из них.

1. Аналитический метод

Задаётся уравнение колебаний гармонического осциллятора

по которому и определяется смещение его от положения равновесия в любой момент времени.

2. Графический метод

Рис.5.3

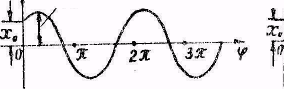
Строятся график гармонического колебания (рис.5.3) х=Аsin(ωt+φ₀). По оси абсцисс (ОХ) откладывается время t или фаза колебаний ωt+φ₀, по оси ординат (ОУ) – смещение х от положения равновесия.

3. Метод векторной диаграммы

Рис.5.4

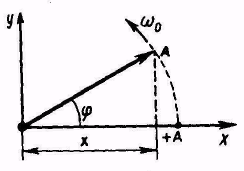
Этот метод состоит в следующем. Гармоническое колебание может быть задано с помощью вектора, длина которого равна амплитуде А колебания, а направление образует с осью х угол, равный начальной фазе колебания (рис. 5.4). Если привести этот вектор во вращение с угловой скоростью ω₀, то проекция конца вектора на ось х будет перемещаться в пределах от +А до -А, а колеблющаяся величина будет изменяться со временем по закону

x = Asin(ω₀t+φ₀), совершая гармоническое колебание.

§ 5.2.2 Скорость и ускорение колеблющейся точки

Чтобы найти скорость материальной точки при гармоническом колебании, возьмем производную от смещения колеблющейся точки x = Asin(ω₀t+φ₀) по времени:

(5.4)

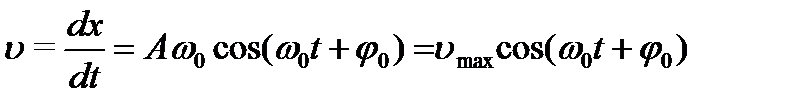
где υ_max = Аω₀ — максимальная скорость (амплитуда скорости).

На основании тригонометрических формул преобразуем (4.18):

(5.5)

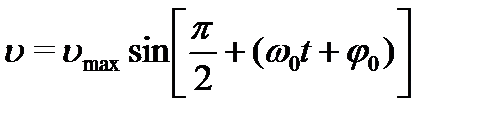
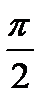
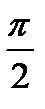
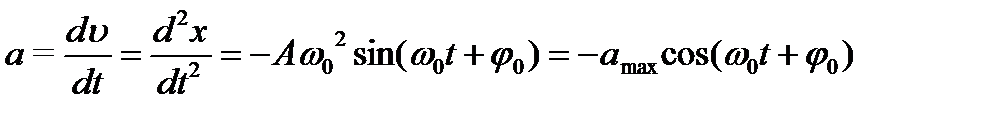
Сравнивая выражения для смещения и скорости замечаем, что фаза скорости на больше фазы смещения, т.е. скорость опережает по фазе смещение на Продифференцировав (5.4), найдем ускорение:

(5.6)

где а_max = А ω₀ 2 — максимальное ускорение (амплитуда ускорения).

Вместо (5.5) запишем

Из сравнения (5.6) и (5.3) следует, что фазы ускорения и смещения различаются на π, т. е. эти величины изменяются в противофазе. Это значит, что при положительном максимальном смещении ускорение максимально, но отрицательно. На рисунке показаны графические зависимости смещения, скорости и ускорения от времени (рис.6.6, а) и их векторные диаграммы (рис.5.6, б) .

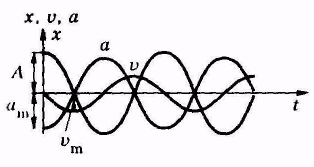
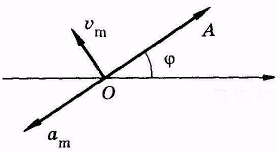
Рис.5.6

б )

а )

§ 5.2.3 Кинетическая и потенциальная энергии колебательного движения

Колеблющееся тело обладает как кинетической, так и потенциальной энергией, которые последовательно переходят друг в друга при колебаниях осциллятора. Полная энергия осциллятора равна сумме кинетической и потенциальной энергии:

Кинетическая энергия тела, колеблющегося по гармоническому закону, вычисляют по формуле:

(5.9)

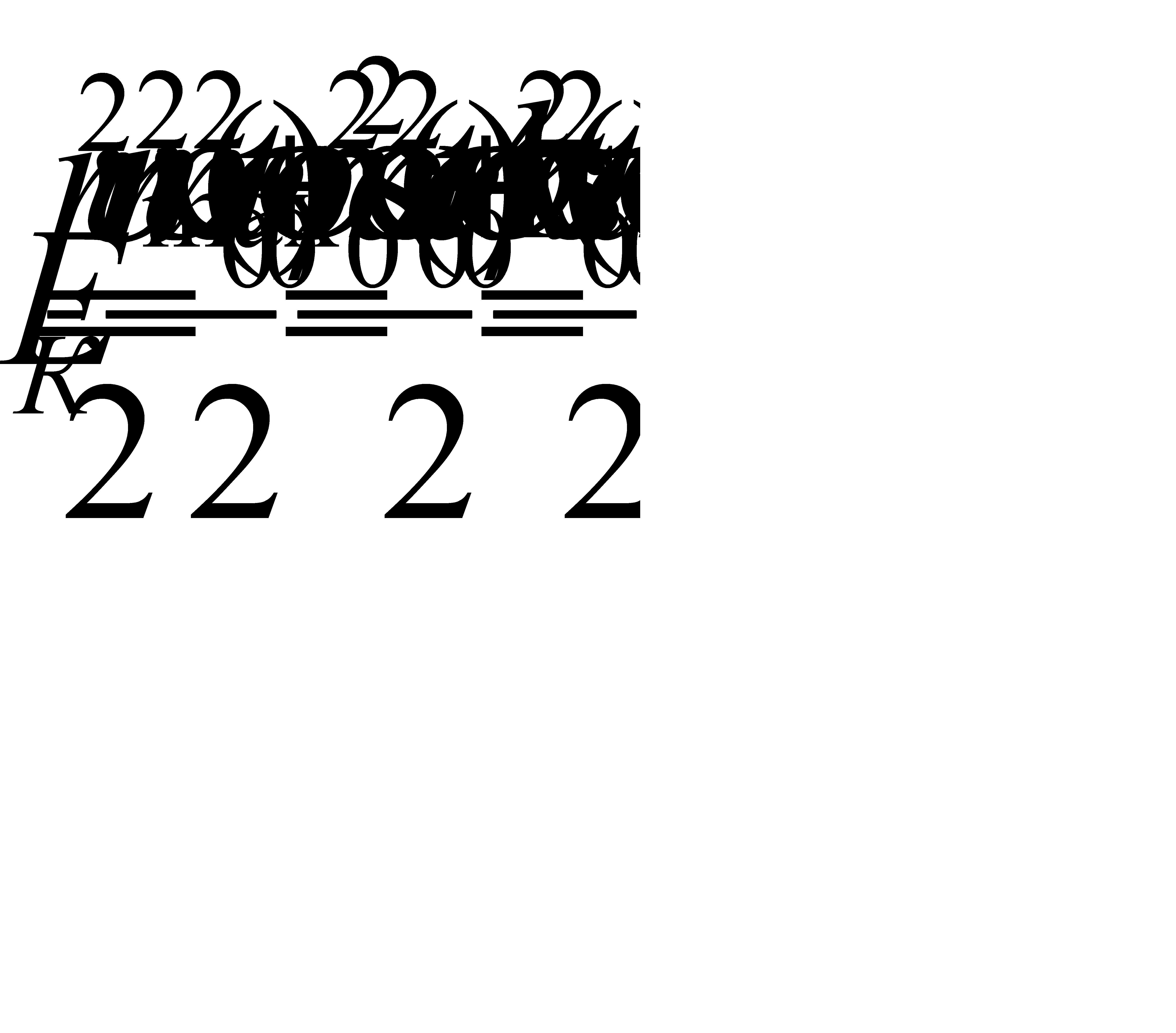
с учётом mω 2 = k

Потенциальную энергию колебательного движения найдём, исходя из формулы для потенциальной энергии упругой деформации:

(5.10)

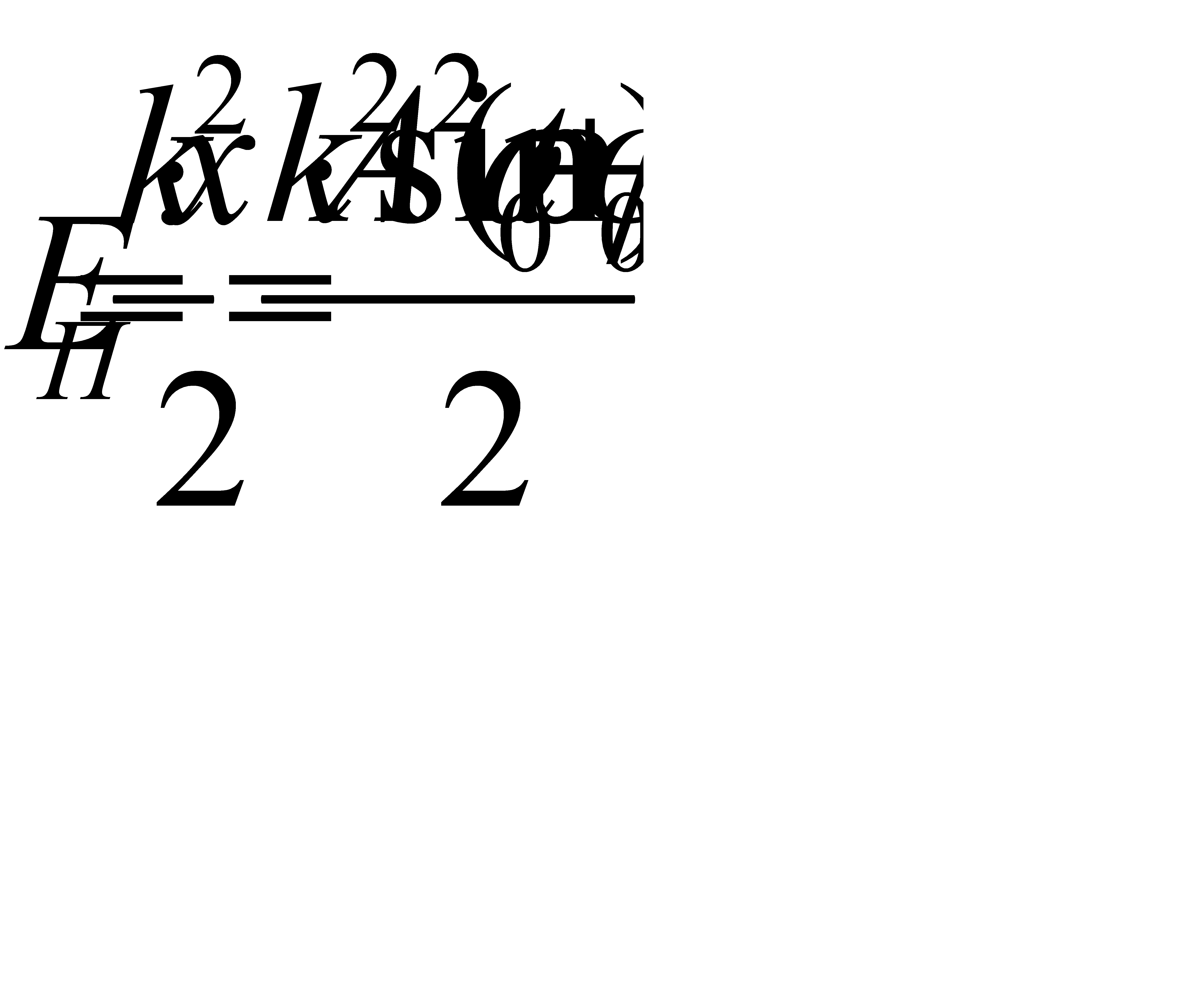
Складывая кинетическую и потенциальную энергию, получим полную механическую энергию материальной точки, колеблющейся по гармоническому закону:

(5.11)

Полученное выражение показывает, что энергия колеблющегося тела от времени не зависит, т.е. с течением времени остаётся величиной постоянной, а зависит только от квадрата амплитуды и частоты.

При отсутствии сил трения полная механическая энергия системы не изменяется:

(5.12)

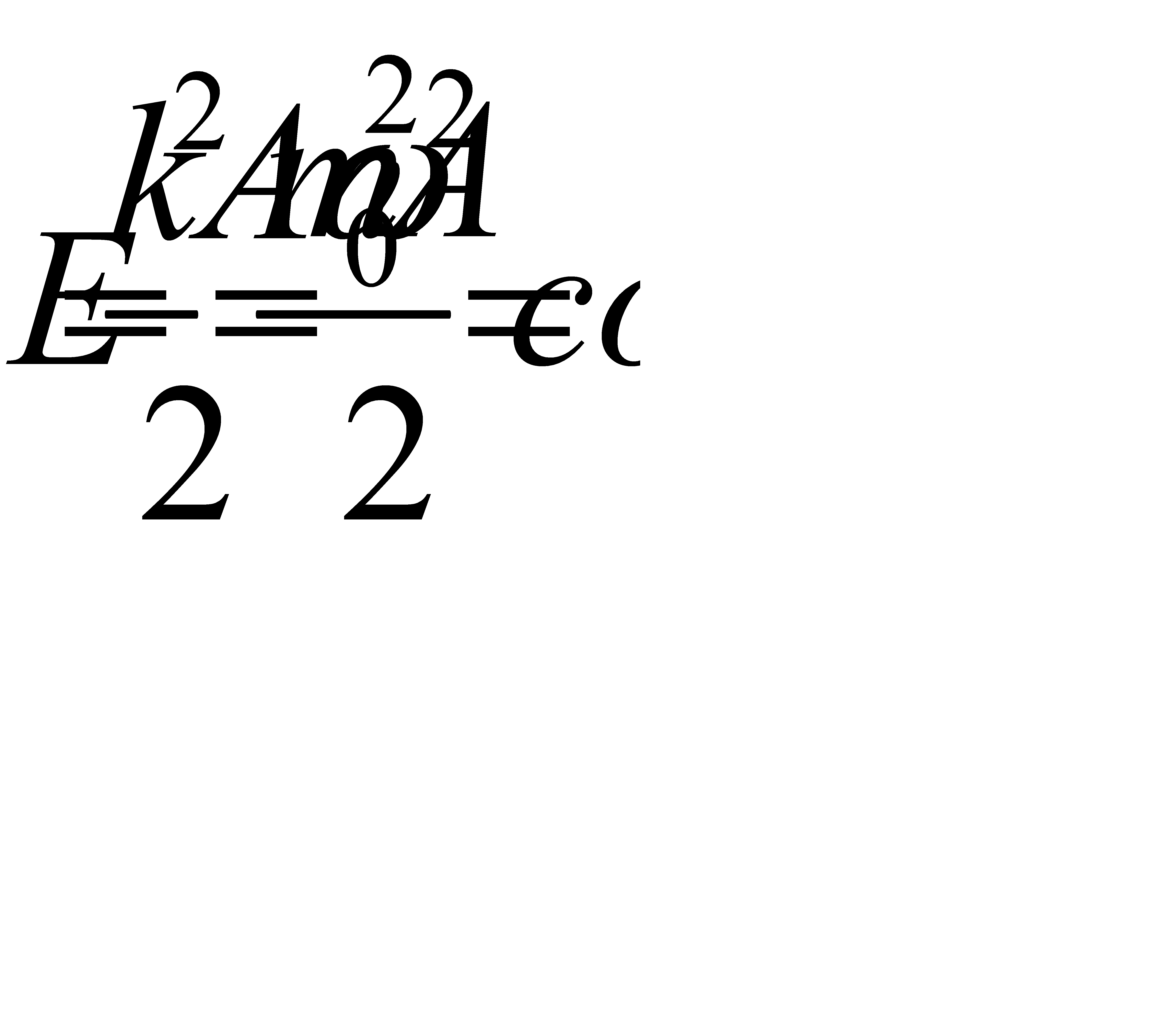
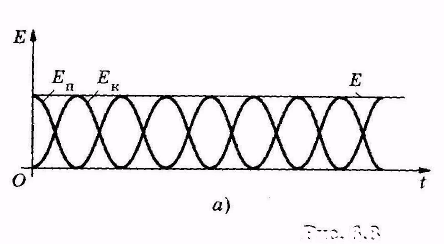
Графически зависимости кинетической, потенциальной и полной механической энергий колеблющейся системы от времени показаны на рис. 5.7, а.

Рис.5.7

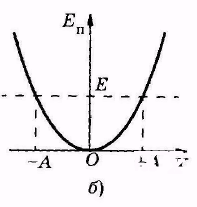
Потенциальная яма (ограниченная область пространства, в которой потенциальная энергия меньше, чем в не её), соответствующая гармоническому колебанию, изображена на рис. 5.7, б. Она определяется зависимостью 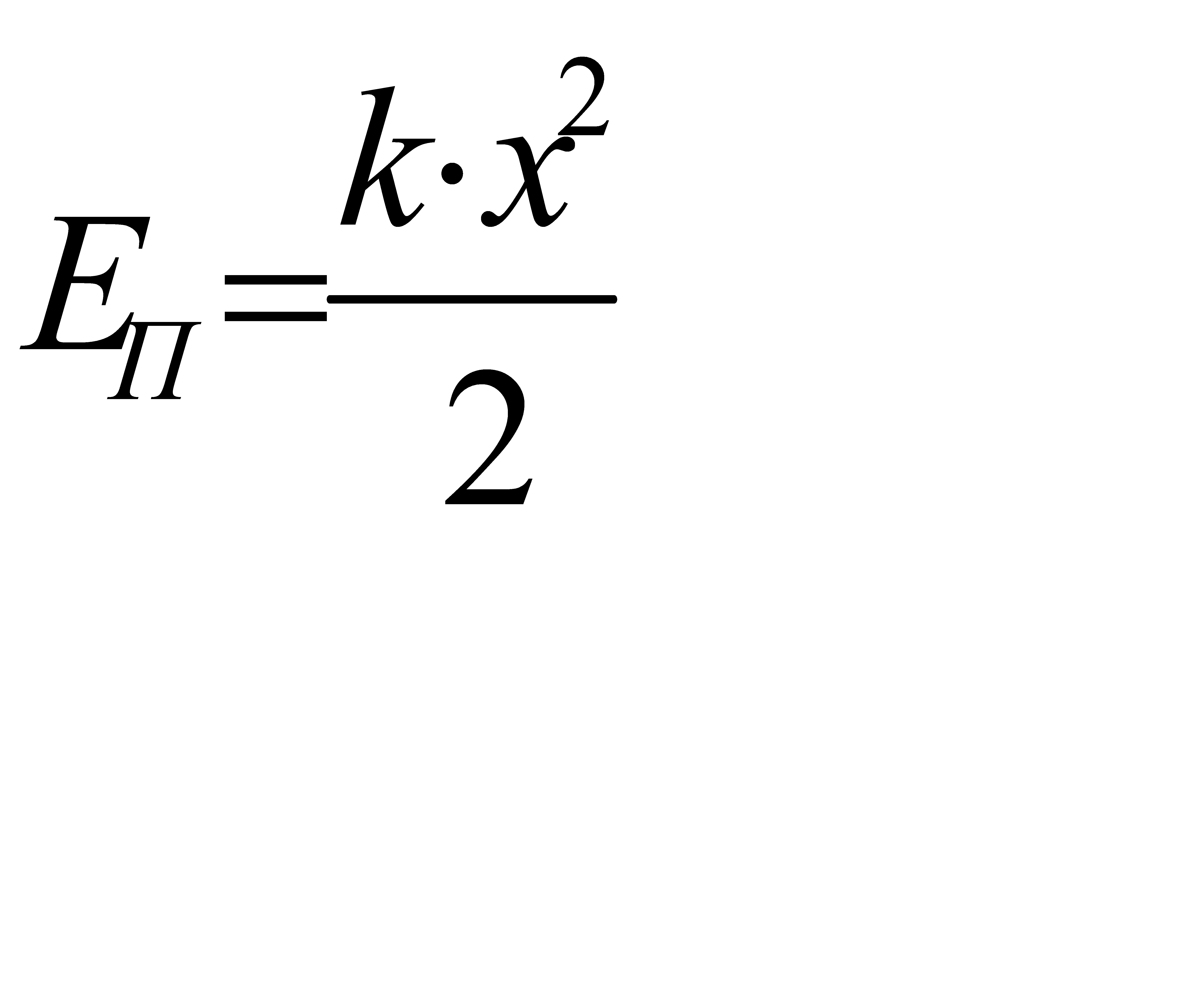. Отложив на оси ординат полную механическую энергию Е, по графику определяют интервал координат (-А, +А), за пределы которого частица, обладающая такой энергией, выйти не может.

§6.2 Затухающие колебания

До сих пор мы рассматривали свободные колебания материальной точки без учёта сопротивления среды, в которой происходят эти колебания.

В реальных условиях на колеблющееся тело всегда действуют силы сопротивления (трения), в результате чего амплитуда с течением времени уменьшается и колебания становятся затухающими.

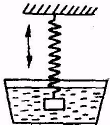
Рис.5.8

Пусть маятник колеблется в вязкой среде (рис.). В этом случае на осциллятор кроме возвращающей силы F_упр = -kx будет действовать ещё одна сила – сила сопротивления среды F_с. При малых колебаниях скорость движения осциллятора мала, поэтому сила сопротивления пропорциональна скорости и направлена в противоположную сторону:

(5.13)

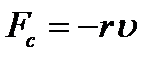
где r – коэффициент сопротивления среды, зависящий от плотности среды и геометрических размеров осциллятора; υ — относительная скорость движения осциллятора и среды.

Уравнение затухающих колебаний записывается в виде:

Выражение А=±А₀ е -δ t , есть переменная во времени амплитуда колебания; А₀— амплитуда в момент t = 0; ω -частота затухающих колебаний; φ₀-начальная фаза колебаний.

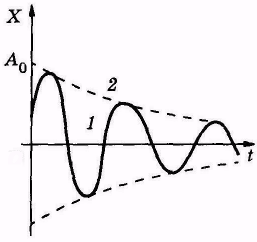
Рис. 6.9

График этой функции изображён на рисунке (кривая 1)пунктирнаялиния 2изображает ход убывания амплитуды. Материальная точка колеблется по закону синуса, но амплитуда колебания с течением времени уменьшается по экспоненте. Затухания происходят тем быстрее, чем больше δ, т.е. с увеличением внутреннего трения среды и уменьшением массы осциллятора.

Наглядной характеристикой затухания является отношение двух амплитуд, отличающихся по времени на период Т. Это соотношение называется декрементом затухания

(5.15)

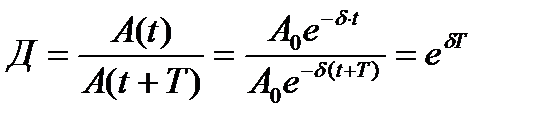
Прологарифмируем это выражение:

(5.16)

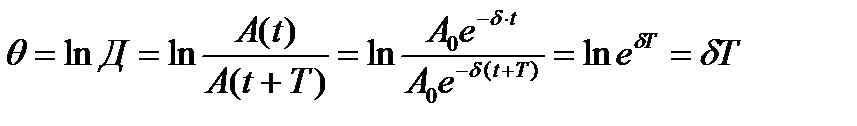
Значение θ=δТ называется логарифмическим декрементом затухания.

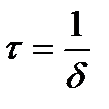
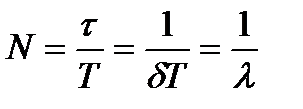
Время в течении которого амплитуда убывает в е раз, называется временем жизни колеблющейся точки. За время жизни τ система успевает совершить N колебаний.

(5.17)

Следовательно, логарифмический декремент затухания есть величина, обратная числу колебаний осциллятора за время его жизни.

Период затухающих колебаний зависит от коэффициента сопротивления rи определяется формулой:

(5.18)

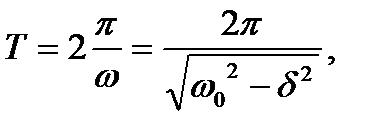
§6.3 Вынужденные колебания. Резонанс

Для того, чтобы колебания осциллятора были незатухающими, надо компенсировать потери энергии на преодоления сопротивления среды. Это можно сделать следующим способом. Пусть пружинный маятник с железным грузом находится в поле тяжести электромагнита, по обмотке которого проходит переменный ток:

Магнитная сила, действующая на маятник, меняется по тому же закону F_в=F₀sinωt. Эта периодически изменяющаяся внешняя сила, действующая на осциллятор, называется вынуждающей силой.

Колебания, возникающие под действием внешней периодически изменяющейся силы, называют вынужденными колебаниями.

Рис.6.11

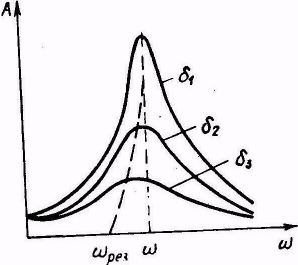
Зависимость амплитуды колебаний от частоты вынуждающей силы при различных δ приведены на рис. При ω → 0 амплитуда стремится к предельной величине, равной смещению осциллятора под действием постоянной силы F₀:

(6.42)

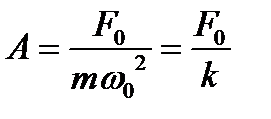
Когда частота вынуждающей силы приближается к частоте собственных колебаний осциллятора, амплитуда колебаний возрастает и при некоторой частоте достигает максимального значения. Это явление называется резонансом.

Существуют и такие колебательные системы, которые сами регулируют периодическое восполнение растраченной энергии и поэтому могут колебаться длительное время. Незатухающие колебания, существующие в какой-либо системе при отсутствии переменного внешнего воздействия, называются автоколебаниями, а сами системы — автоколебательными. Амплитуда и частота автоколебаний зависят от свойств самой автоколебательной системы, в отличие от вынужденных колебаний они не определяются внешними воздействиями.

Классическим примером механической автоколебательной системы являются часы, в которых маятник (или баланс) является колебательной системой, пружина (или поднятая гиря) — источником энергии, а анкер — регулятором поступления энергии от источника в колебательную систему. Некоторые биологические системы (сердце, легкие) являются автоколебательными.

Дата добавления: 2015-12-08 ; просмотров: 1885 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

2)Гармонические колебания (рис.2.4.).

Его параметрами являются: A_m – амплитуда ,  — частота, ₀ –начальная фаза. Это пример непрерывного сигнала.

Непериодические сигналы – это сигналы, которые описываются непериодическими функциями времени. Однако их можно рассматривать как периодические, для которых Т .

Примеры непериодических сигналов.

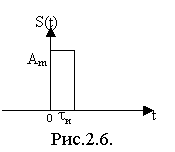
1) Сигнал типа единичная функция (ступенчатый сигнал, функция Хевисайда, рис.2.5.).

2) Одиночный прямоугольный импульс – это сигнал, форма которого прямоугольная (рис.2.6).

3) Сигнал типа (дельта – функция, функция Дирака, рис. 2.7.).

0, t 0

Эта функция обладает свойствами: 1.;

2.-это

соотношение называют, фильтрующее свойство дельта – функции.

Случайные сигналы – это сигналы характер изменения, которых заранее предсказать невозможно. Именно эти сигналы несут информацию о состоянии интересующего нас объекта. С математической точки зрения такие сигналы описываются методами теории вероятности или случайных процессов. Разновидностью случайных сигналов являются помехи – сигналы, которые накладываются на передаваемые сообщения и искажают его характер. По природе происхождения помехи бывают: атмосферные, индустриальные и флуктуационные.

Флуктуационные помехи связаны , с хаотичным движением свободных носителей зарядов в самих элементах электрических цепей.

2.2. Гармоническое колебание и способы его представления

Гармоническим называется колебание, которое описывается гармонической функцией времени: sin(t), cos(t).

Гармоническое колебание, а также сигнал произвольной формы могут быть представлены в следующих формах:

1) временное представление сигнала;

2) комплексное представление;

3) векторное представление;

1) При временном представлении сигнал записывается в виде аналитической функцией времени: .

Его график – называется временной диаграммой (рис.2.8.). Основными параметрами гармонического сигнала являются:

Амплитуда — A_m (наибольшее отклонение от нуля гармонической функции). Размерность амплитуды связана с физической природой сигнала.

2. Период — T (минимальное расстояние между точками находящимися в одной фазе), ω=2π/T — круговая частота, f=1/T – циклическая частота. Их размерность: T  [сек]; f  [Гц]; ω  [рад/сек].

₀=ωt₀ – начальная фаза гармонического колебания гармонического колебания; t₀ – временной сдвиг, если t₀>0, то это означает опережение, если t₀ 2 +b 2 ) 1/2 — длины вектор комплексного числа.

φ =arg[Z] – аргумент комплексного числа Z, или φ₀ = arctg(b/a) – начальная фаза.

Выражение А_me j ( ωt + φ ) называют комплексом гармонической функции. Тогда учитывая, что Аcosφ = Re, можно записать

Комплексную величину называют комплексной амплитудой гармонического сигнала, а е j ω t – множитель вращения. Комплексная амплитуда содержит информацию о двух важнейших параметрах гармонического сигнала – об амплитуде и о начальной фазе. Комплексная амплитуда и гармоническая функция времени, при известной частоте ω, связаны взаимнооднозначно, т. е.

.

Например: гармоническому колебанию u(t)=256cos(2π100t — 45 0 ) соответствует комплексная амплитуда — Ù_m = 256e — j 45 , справедливо и обратное.

3) Векторное представление сигнала – это представление сигнала вектором на комплексной плоскости. Рассмотрим векторное представление следующих сигналов:

а) комплексное гармоническое колебание — гармонический комплекс:

где e jωt – множитель вращения.

На комплексной плоскости гармонический комплекс представляется вектором А_m c начальной фазой -φ₀, который вращается против часовой стрелки с частотой ω.

б) гармоническое колебание s(t) = A_mcos(ωt- φ₀)= Re<À_me j ωt >.

На комплексной плоскости гармоническое колебание представляется проекцией вращающегося с частотой ω против часовой стрелки вектора гармонического комплекса на реальную ось.

в) Комплексная амплитуда . На комплексной плоскости она представляется в виде неподвижного вектора с амплитудой A_m и начальной фазой -₀.

Спектральное представление сигнала.

Операторное представление сигнала.

Два последних способа описания сигнала рассмотрим подробнее.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник