- 2)Гармонические колебания (рис.2.4.).
- 2.2. Гармоническое колебание и способы его представления
- 1) При временном представлении сигнал записывается в виде аналитической функцией времени: .
- 3.1 Представление гармонических функция с помощью комплексных величин
- 1. Преимущества переменного тока
- 2. Способы представления гармонических функций
2)Гармонические колебания (рис.2.4.).
Его параметрами являются: Am – амплитуда , — частота, 0 –начальная фаза. Это пример непрерывного сигнала.
Непериодические сигналы – это сигналы, которые описываются непериодическими функциями времени. Однако их можно рассматривать как периодические, для которых Т 
Примеры непериодических сигналов.
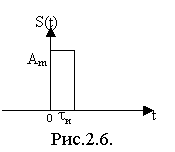
1) Сигнал типа единичная функция (ступенчатый сигнал, функция Хевисайда, рис.2.5.).
2
3) Сигнал типа 

Э

2.
соотношение называют, фильтрующее свойство дельта – функции.
Случайные сигналы – это сигналы характер изменения, которых заранее предсказать невозможно. Именно эти сигналы несут информацию о состоянии интересующего нас объекта. С математической точки зрения такие сигналы описываются методами теории вероятности или случайных процессов. Разновидностью случайных сигналов являются помехи – сигналы, которые накладываются на передаваемые сообщения и искажают его характер. По природе происхождения помехи бывают: атмосферные, индустриальные и флуктуационные.
Флуктуационные помехи связаны , с хаотичным движением свободных носителей зарядов в самих элементах электрических цепей.
2.2. Гармоническое колебание и способы его представления
Гармоническим называется колебание, которое описывается гармонической функцией времени: sin(t), cos(t).
Г
1) временное представление сигнала;
2) комплексное представление;
3) векторное представление;
1) При временном представлении сигнал записывается в виде аналитической функцией времени: .
Его график – называется временной диаграммой (рис.2.8.). Основными параметрами гармонического сигнала являются:
Амплитуда — Am (наибольшее отклонение от нуля гармонической функции). Размерность амплитуды связана с физической природой сигнала.
2. Период — T (минимальное расстояние между точками находящимися в одной фазе), ω=2π/T — круговая частота, f=1/T – циклическая частота. Их размерность: T [сек]; f [Гц]; ω [рад/сек].
0=ωt0 – начальная фаза гармонического колебания гармонического колебания; t0 – временной сдвиг, если t0>0, то это означает опережение, если t0 2 +b 2 ) 1/2 — длины вектор комплексного числа.
φ =arg[Z] – аргумент комплексного числа Z, или φ0 = arctg(b/a) – начальная фаза.
Выражение Аme j ( ωt + φ ) называют комплексом гармонической функции. Тогда учитывая, что Аcosφ = Re
Комплексную величину 

Например: гармоническому колебанию u(t)=256cos(2π100t — 45 0 ) соответствует комплексная амплитуда — Ùm = 256e — j 45 , справедливо и обратное.
3) Векторное представление сигнала – это представление сигнала вектором на комплексной плоскости. Рассмотрим векторное представление следующих сигналов:
а) комплексное гармоническое колебание — гармонический комплекс:
где e jωt – множитель вращения.
На комплексной плоскости гармонический комплекс представляется вектором Аm c начальной фазой -φ0, который вращается против часовой стрелки с частотой ω.
б) гармоническое колебание s(t) = Amcos(ωt- φ0)= Re<Àme j ωt >.
На комплексной плоскости гармоническое колебание представляется проекцией вращающегося с частотой ω против часовой стрелки вектора гармонического комплекса на реальную ось.
в) Комплексная амплитуда 
Спектральное представление сигнала.
Операторное представление сигнала.
Два последних способа описания сигнала рассмотрим подробнее.
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Источник
3.1 Представление гармонических функция с помощью комплексных величин
Расчеты электрических цепей гармонического тока в тригонометрической форме или графически с помощью векторных диаграмм применяются на практике только в случае простых схем.
С усложнением электрических цепей, с увеличением числа контуров, источников энергии, добавлением взаимных индуктивностей и т. д. тригонометрические или графические расчеты становятся крайне затруднительными. Требуется метод, позволяющий рассчитывать электрические цепи переменного тока алгебраически, аналогично цепям постоянного тока. Таким удобным расчетным методом служит метод комплексных амплитуд (комплексный метод), введенный в электротехнику А. Е. Кеннеди и П. Ч. Штейнметцом в 1893 – 1894 гг. Этот метод, как и векторные диаграммы, основан на представлении гармонических функций в виде проекций вращающихся векторов, причем вращающиеся векторы выражаются аналитически, в комплексной форме. Алгебраически интерпретируя векторные диаграммы, этот метод удобно сочетает аналитические расчеты с геометрическими представлениями.
Все последующее изложение данного курса и радиотехнических дисциплин базируется на этом методе.
Известно, что каждая точка на комплексной плоскости определяется радиусом-вектором этой точки, т. е. вектором, начало которого совпадает с началом координат, а конец находится в точке, соответствующей заданному комплексному числу (рисунок 3.1).
Пользуясь показательной или полярной формой записи комплексного числа, имеем
Здесь А – модуль;


Применив формулу Эйлера, можно получить тригонометрическую форму записи комплексного числа
Вектор, вращающийся в положительном направлении, т.е. против хода часовой стрелки, с угловой скоростью ω, может быть выражен следующим образом
где 

Записывая комплексную функцию (3.1) в тригонометрической форме
заключаем, что гармоническая функция Acos( ω t+a) может рассматриваться как действительная часть комплексной функции (3.1), или, что то же, как проекция вращающегося век-тора на действительную ось.
Условно это записывается так:
Символ Re обозначает, что берется действительная часть комплексной функции. Например,
где 
Аналогично функция Asin( ω t+ ψ ) может быть в случае необходимости представлена как мнимая часть комплексной функции (3.1), взятая без множителя j, или как проекция вращающегося вектора на мнимую ось.
Условно это записывается так
где символ Im обозначает, что берется мнимая часть комплексной функции. Например,
Другой способ представления гармонической функции с помощью комплексных величин основан на применении формул
Согласно (3.2) можно заключить, что функция Acos( ω t+ ψ ) равна геометрической сумме двух комплексно сопряженных векторов, имеющих модуль A/2 и вращающихся в противоположные стороны с одинаковой угловой скоростью ω.
В результате сложения таких двух векторов получается вектор, расположенный на действительной оси, т. е. для любого момента времени t получается действительная величина (рисунок 3.3, а).
Аналогично из (3.3) видно, что функция Asin(ωt+ ψ ) равна геометрической разности тех же двух вращающихся векторов, деленной на j. Разность этих векторов для любого момента времени t представляет мнимую величину (рисунок 3.3, б), и поэтому ее делят на j для получения действительной функции.

Вращение вектора в отрицательном направлении (по ходу часовой стрелки) связано с понятием отрицательной круговой частоты (– ω ), которое является чисто математическим понятием, вытекающим из вышеприведенных формул. Введение этого понятия в ряде случаев удобно для исследования процессов в электрических цепях. Из сравнения построения на рисунках 3.3, а и б, видно, что представление гармонических функций с помощью двух векторов, вращающихся в противоположные стороны, для функции вида Acos( ω t+ ψ ) проще, чем для функции Asin( ω t+ ψ ).
Источник
1. Преимущества переменного тока
2. Способы представления гармонических функций
3. Действующие и средние значения гармонических величин
Поддается трансформации, отсюда возможность передачи на большие расстояния.
Производство переменного тока просто и рационально.
Потребитель при переменном токе легче решает вопросы преобразования электрической энергии в механическую.
Преимущества синусоидальной формы кривых тока и напряжения перед другими периодическими формами:
форма кривых после трансформации не меняется; величины меняются плавно, нет перенапряжений, толчков тока, кото-
рые недопустимы в энергетике.
Существует несколько способов представления гармонических функ-
1. Графическое изображение – синусоида ( рис.5.1 ).
i
Значение переменной величины в данный момент называют мгновенным. Мгновенные значения обозначают строчными буквами i, u , e .
Теоретические основы электротехники. Конспект лекций
ЛЕКЦИЯ 5. СПОСОБЫ ИЗОБРАЖЕНИЯ И ПАРАМЕТРЫ СИНУСОИДАЛЬНЫХ ЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
2. Способы представления гармонических функций
Наименьший промежуток времени, через который мгновенные значения повторяются, называют периодом Т :
Период – время одного полного колебания. Величину, обратную периоду, называют частотой f :
Частота – число полных колебаний в единицу времени:
[ f ] = 1 с = с − 1 = Гц.
Промышленная частота в России – 50 Гц, в США, Японии – 60 Гц. Была выбрана частота, которая представлялась оптимальной. Нижний предел определяли требованиями освещения (чтобы не были заметны отключения при нулевых значениях тока), верхний – требуемой скоростью вращения валов электродвигателей, которая пропорциональна частоте. В настоящее время такие значения частоты признаны неудачными. При увеличении частоты уменьшаются вес и габариты оборудования. На переход к другой частоте повсеместно нет материальных ресурсов. Когда необходимо уменьшить вес и габариты устройств, используют преобразователи частоты (на лесоповале для питания используют напряжение частотой 400 Гц) или автономные источники (в самолетах напряжение частотой несколько тысяч Гц).
2. Изображение тригонометрическими функциями.
Мгновенные значения электрических величин являются синусоидальными функциями времени:
i = I m sin ( ω t + ψ i ) ; u = U m sin ( ω t + ψ u ) ; e = E m sin ( ω t + ψ e ) ,
где i, u, e – мгновенные значения; I m ,U m , E m – максимальные (амплитудные) значения (см. рис. 5.1 ); (ω t + ψ) – фаза колебания, характеризующая развитие
процесса во времени; ω t
– текущий угол, который отсчитывают от начала
Источник