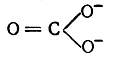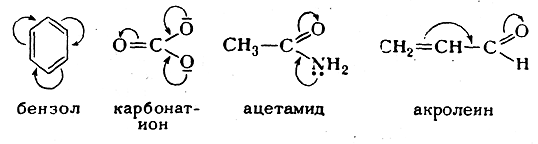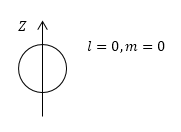Способы представления электронной плотности

Способы изображения распределения электронной плотности в молекулах

Как уже указывалось на примере молекулы бензола, классические структурные формулы ароматических соединений и соединений алифатического ряда с сопряженными связями, правильно передавая последовательность связи атомов (химическое строение), в одном отношении недостаточны: эти формулы не отражают истинного распределения электронной плотности. Так, например, из классической формулы карбонат-аниона следует, что с атомом углерода простой связью связаны

два равноценных атома кислорода, несущих отрицательные заряды, а двойной связью — нейтральный атом кислорода. В действительности же все три атома кислорода в карбонат-анионе равноценны: все три межатомных расстояния С—О одинаковы, а два отрицательных заряда равномерно распределены между тремя атомами кислорода.

В настоящее время наиболее распространены три способа изображения распределения электронной плотности в молекулах.

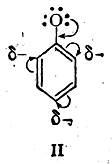
Сущность первого заключается в том, что в классические структурные формулы вводится поправка с помощью изогнутых стрелок, указывающих направление, в котором смещены электроны (сравнительно с той картиной распределения электронной плотности, которую дает классическая структурная формула). Ранее этим способом изображена карбонильная группа; ниже приведены формулы бензола, карбонат-аниона, ацетамида и акролеина:

Рассматриваемый способ в большинстве случаев удобен, о чем, в частности, свидетельствует его широкое применение в химической литературе. Однако этот способ имеет и недостатки. Неудобство его заключается прежде всего в том, что такими же изогнутыми стрелками изображаются также смещения электронов в момент реакции (электромерные смещения), а иногда и сумма обоих эффектов — статического и динамического. Кроме того, количественно неравноценные электронные смещения выражаются совершенно одинаково.

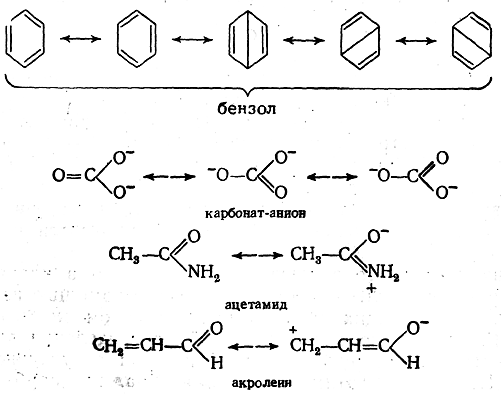
Второй возможный способ изображения распределения электронной плотности в молекулах заключается в том, что выписываются несколько возможных классических структурных формул для данной молекулы (между этими структурами ставятся обоюдоострые стрелки); при этом принимается, что истинное строение молекулы является промежуточным, «гибридным», между этими «предельными структурами» и описывается их совокупностью, например:

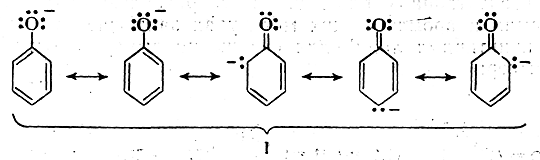
Многоструктурный способ изображения распределения электронной плотности в молекулах в большинстве случаев мало удобен сравнительно с другими предложенными. Так, например, формула (I) фенолят-аниона представляла бы в соответствии с этим способом комбинацию из пяти предельных структур:

в то время как ее гораздо удобнее написать, используя изогнутые стрелки:

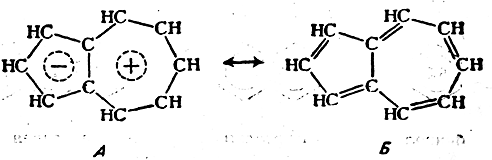
Однако можно привести отдельные примеры, когда многоструктурный способ написания формул, по-видимому, является более наглядным. Так, химик, написав для молекулы азулена две структуры — биполярную (А) и классическую (Б), по-видимому, наиболее просто может представить себе строение этой молекулы как промежуточное между двумя написанными «крайними», предельными, структурами:

Изобразить структуру азулена формулой, подобной формуле II фенолят-аниона, с использованием изогнутых стрелок весьма сложно.

При многоструктурном способе написания формул можно иногда дать некоторое представление о величине электронного смещения, указав для каждой структуры коэффициент при функции ψ), рассчитанный по методу электронных пар. Однако надо иметь в виду, что чем сложнее молекула, тем менее надежны такие расчеты.

Наконец, третий возможный способ изображения распределения электронной плотности в сопряженных алифатических системах и ароматических молекулах заключается вприменении пунктирных линий для отражения выравненности связей, например:

Для изображения ароматических систем в настоящее время все чаще применяют не пунктирные, а сплошные линии, например:

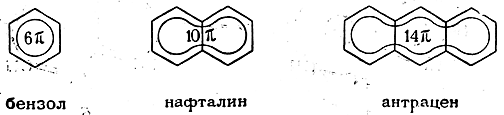
Иногда в формулах такого рода указывают число обобщенных π-электронов, а в конденсированных ароматических системах вписывают не изолированные окружности, а сплошные кривые, символизирующие общие π-электронные облака, например:

В настоящее время последний из трех рассмотренных способов изображения распределения электронной плотности, несмотря на некоторую его необычность, быстро приобретает широкое распространение ввиду его наибольшей наглядности.

Источник

Представление о распределении объемного заряда и электростатического потенциала в атоме

Вы будете перенаправлены на Автор24

Распределение плотности электронного облака в атоме водорода

Рассмотрим пространственную структуру атома водорода в стационарном состоянии.

Вероятность нахождения электрона в элементе объема:

возле точки с координатами $r,\theta ,\varphi $ равна:

где квантовые числа опустим для сокращения записи, $R(r)$ — радиальная функция, $Y\left(\theta ,\varphi \right)-угловая\ фунекиция$. Вероятности (2) ставят в соответствие представление об электроне в виде облака, которое имеет плотность. Причем эта плотность пропорциональна $<\left|\psi(r,\theta ,\varphi )\right|>^2$. Величина $q_e<\left|\psi(r,\theta ,\varphi )\right|>^2=\rho $ называется плотностью заряда электрона и считается непрерывно распространенной в пространстве. Часто используют следующую интерпретацию: Полагают, что электрон обегает пространство, которое занимает атом, при этом время пребывания электрона в объеме dV пропорционально$<\left|\psi(r,\theta ,\varphi )\right|>^2.$

Структура электронного облака задает пространственную конфигурацию атома. Часто, для упрощения, рассматривают радиальное и угловое распределения плотности облака отдельно.

Вероятность обнаружить электрон в шаровом слое $r\ и\ r+dr\ $ равна:

Плотность вероятности для координаты r при этом описано функцией:

Используя радиальные волновые функции ($R_$) в явном виде для состояний атома водорода можно из выражения (4) найти зависимости плотности электронного облака от расстояния $(r)$. Отметим, что вероятность обнаружения электрона очень близко к ядру и на больших расстояниях от ядра мала. Плотность облака существенна на конечных расстояниях от ядра.

Нахождение средних расстояний дает формулу:

где $r_B$ — Боровский радиус.

Из формулы (5) видно, что $\left\langle r_\right\rangle $ растер при увеличении $n$ (главного квантового числа), при установленном $n$ уменьшается в зависимости от роста орбитального квантового числа ($l$).

Четкой границы у атома не существует, но плотность электронного облака по экспоненте уменьшается при $r >\left\langle r\right\rangle $. В состоянии $l=n-1$ имеем:

Готовые работы на аналогичную тему

Рассмотрим угловое распределение электронного облака. Вероятность нахождения электрона в пределах элемента телесного угла ($d\Omega =sin\theta d\theta d\varphi $) в направлении, которое задается углами $\theta $ и $\varphi $ равна:

При этом плотность вероятности равна:

Функция $Y_\sim e^$, следовательно $p_$ от угла $\varphi $ не зависит. Следовательно, электронное облако имеет осевую симметрию.

Распределение по полярному углу $\theta $ обычно представляют графически в полярных диаграммах. При этом на полярной оси от начала координат откладывают величины $p_$. Через полученные точки проводят линию. Чем дальше точки от начала координат, тем выше вероятность найти частицу в исследуемом направлении.

Для больших величин $n\ и\ l$ строение атома водорода весьма сложное.

Плотность электронного облака в атоме со многими электронами

Пусть пара сопряженных величин: координата $q$ и импульс $p$ определяют координаты точки в $pq$ — плоскости. Перейдя к движению в пространстве, имеем три координаты и три импульса ($6$-мерное пространство). Положим, что все электроны в атоме имеют одинаковые условия. Каждый электрон подчинен закону сохранения энергии (его потенциальная энергия равна $q_e\varphi ,\ \varphi $ — средний потенциал). В каждой ячейке объемом $h^3$ может находиться только два электрона, при этом максимальный их имеющихся импульсов равен $p_$. Плотность электронов можно выразить как ($p \[\rho =-\frac<8\pi q_e><3><\left(\frac>\right)>^3\left(9\right).\]

Электростатический потенциал в атоме

Если известны, плотность заряда ($\rho $) и импульс ($p_$), то их можно связать с электростатическим потенциалом ($<\varphi >_e$). Для этого используется уравнение Пуассона, считая, что $\rho $ и $<\varphi >_e$ симметричны относительно ядра и зависят только от расстояния до него. Данное уравнение принимает вид:

Из закона сохранения энергии имеем:

Принимая во внимание то, что в атоме связаны только те электроны, для которых работа, требуемая для переноса их на поверхность атома, положительна. Рассматривая ионы с зарядом равным $Zq_e,$ вводим сферу радиуса $R$, вне которой потенциал имеет кулоновский вид:

Этот потенциал учитывается при подсчете работы, которая необходима для удаления электрона. Будем считать, что $E=0$ для электрона на этой сфере, получаем для максимального импульса выражение:

На потенциал накладываются граничные условия вида:

Так как около ядра вклад электронов в потенциал несущественный, то следующее граничное условие запишем как:

Подставим выражение (11) в формулу (9) получаем:

Если умножить выражение (14) на $\frac<1><<\varepsilon >_0>$, то получим правую часть уравнения Пуассона. То есть (10) примет вид:

Уравнение Пуассона содержит одну неизвестную функцию.

Задание: На каком расстоянии от ядра $(r)$ в состоянии с орбитальным квантовым числом $l=n-1$ плотность вероятности обнаружить электрон максимальна? Рассмотреть атом водорода в стационарном состоянии.

Решение:

В состояниях с $l=n-1$ функция плотности вероятности для атома водорода в стационарном состоянии имеет вид:

Для нахождения экстремума функции возьмем производную от $p\left(r\right)$ по $r$ приравняем ее к нулю:

Ответ: Максимума функция $p\left(r\right)$ достигает в точке $<\rm r><\rm =>n^2r_B.$ Расстояния совпадают с радиусами круговых орбит.

Задание: Рассмотрите состояния атома водорода, которые описываются угловыми функциями: $Y_<00>=\frac<1><\sqrt<4\pi >>,\ Y_<10>=\sqrt<\frac<3><4\pi >>cos\theta $. Изобразите полярные диаграммы. Чему равна вероятность нахождения электрона на полярной оси?

Решение:

Рассмотрим функцию $Y_<00>=\frac<1><\sqrt<4\pi >>$. Из формулы видим, что $l=0,\ m=0.$ В s — состоянии облако имеет сферическую симметрию (рис.1).

Для функции $Y_<10>=\sqrt<\frac<3><4\pi >>cos\theta $ имеем $l=1,\ m=0.$ В $p$ — состоянии при $m=0$ электронное облако вытянуто по оси $Z$ (рис.2).

Ответ: На полярной оси вероятность обнаружить электрон равна нулю.

Источник

Электронная плотность

Из Википедии — свободной энциклопедии

Рассмотрим водородоподобный атом — систему из двух зарядов: положительно заряженного тяжёлого ядра, и электрона, вероятность обнаружения которого распределена сферически симметрично вокруг ядра. Таким образом, у атома водорода (и ему подобных) в основном состоянии электронная плотность зависит только от расстояния до ядра и одинакова в любой точке сферы. Это состояние электрона характеризуется нулевым орбитальным моментом импульса (так называемое s-состояние). В возбуждённых состояниях с отличным от нуля орбитальным моментом электрона (p-, d-, f-… состояния) сферическая симметрия электронной плотности отсутствует. В достаточно сложных молекулах электронная плотность, как правило, несимметрична, а форма электронного облака может меняться. Например, при замещении трёх атомов водорода метильной группы уксусной кислоты на чрезвычайно электроотрицательные атомы хлора её константа диссоциации (pK) снижается с 4,76 до почти 1 в результате индуктивно вызванного снижения силы притяжения H + к карбоксильной группе; сила кислоты возрастает. Существуют две простые, но логичные точки зрения на это явление. По одной из них, увеличение силы кислоты отражает смещение плотности распределения единственного избыточного электрона карбоксильного кислорода в сторону от H+, и сила притяжения протона ослабевает. Согласно другой точке зрения, причиной этого явления служит не смещение, а «разжижение» «облака отрицательного электричества», то есть снижение электронной плотности вокруг однозарядного атома кислорода.

В качестве модели состояния электрона в атоме, в квантовой механике принято представление об электронном облаке, плотность соответствующих участков которого пропорциональна вероятности нахождения там электрона.

Электронное облако часто изображают в виде граничной поверхности. При этом обозначение электронной области при помощи точек опускают. Пространство вокруг ядра, в котором наиболее вероятно пребывание электрона, называют атомной орбиталью (смысл которого вытекает из волнового уравнения Шрёдингера).

Применяются графические изображения распределения электронной плотности относительно ядра.

Кривая радиального распределения вероятности показывает, что электрон находится в тонком концентрическом шаровом слое радиуса r толщины dr вокруг ядра атома водорода [1] .

Проекция максимума кривой соответствует боровскому радиусу α₀=0,53 Å.

Во многих случаях для решения уравнения Шрёдингера используют различные приближения. Вероятностную (статистическую) интерпретацию волновой функции разработал Макс Борн. В 1954 году М.Борн удостоен Нобелевской премии по физике с формулировкой «За фундаментальные исследования в области квантовой механики, особенно, за статистическую интерпретацию волновой функции.»

Источник

Электронная плотность

• Электро́нная пло́тность — плотность вероятности обнаружения электрона в данной точке конфигурационного пространства.

Рассмотрим водородоподобный атом — систему из двух зарядов: положительно заряженного тяжёлого ядра, и электрона, вероятность обнаружения которого распределена сферически симметрично вокруг ядра. Таким образом, у атома водорода (и ему подобных) в основном состоянии электронная плотность зависит только от расстояния до ядра и одинакова в любой точке сферы. Это состояние электрона характеризуется нулевым орбитальным моментом импульса (так называемое s-состояние). В возбуждённых состояниях с отличным от нуля орбитальным моментом электрона (p-, d-, f-… состояния) сферическая симметрия электронной плотности отсутствует.

В достаточно сложных молекулах электронная плотность, как правило, несимметрична, а форма электронного облака может меняться. Например, при замещении трёх атомов водорода метильной группы уксусной кислоты на чрезвычайно электроотрицательные атомы хлора её константа диссоциации (pK) снижается с 4,76 до почти 1 в результате индуктивно вызванного снижения силы притяжения H+ к карбоксильной группе; сила кислоты возрастает. Существуют две простые, но логичные точки зрения на это явление. По одной из них, увеличение силы кислоты отражает смещение плотности распределения единственного избыточного электрона карбоксильного кислорода в сторону от H+, и сила притяжения протона ослабевает. Согласно другой точке зрения, причиной этого явления служит не смещение, а «разжижение» «облака отрицательного электричества», то есть снижение электронной плотности вокруг однозарядного атома кислорода.

В качестве модели состояния электрона в атоме, в квантовой механике принято представление об электронном облаке, плотность соответствующих участков которого пропорциональна вероятности нахождения там электрона.

Электронное облако часто изображают в виде граничной поверхности. При этом обозначение электронной области при помощи точек опускают. Пространство вокруг ядра, в котором наиболее вероятно пребывание электрона, называют атомной орбиталью (смысл которого вытекает из волнового уравнения Шрёдингера).

Применяются графические изображения распределения электронной плотности относительно ядра.

Кривая радиального распределения вероятности показывает, что электрон находится в тонком концентрическом шаровом слое радиуса r толщины dr вокруг ядра атома водорода.

Проекция максимума кривой соответствует боровскому радиусу α0=0,53 Å.

Во многих случаях для решения уравнения Шрёдингера используют различные приближения. Вероятностную (статистическую) интерпретацию волновой функции разработал Макс Борн. В 1954 году М.Борн удостоен Нобелевской премии по физике с формулировкой «За фундаментальные исследования в области квантовой механики, особенно, за статистическую интерпретацию волновой функции.»

Источник