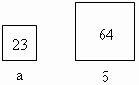Урок математической статистики на тему «Представление данных»
Тип урока: Объяснение нового материала
Формирование у учащихся представления о простейших статистических характеристиках.
Обработка статистических данных.
Наглядная интерпретация статистической информации.
Формирование у учащихся единой научной картины мира и элементов научного мировоззрения.
Способствовать формированию у учащихся чувства коллективизма, ответственности за общее дело в ходе групповой работы.
Оборудование: мультимедиа-проектор, компьютер.
1. Знакомство учащихся с темой урока целесообразно построить в форме беседы.
Слово учителя ( зачитывается отрывок из романа Ильфа и Петрова «Двенадцать стульев»
«Статистика знает всё» известно, сколько какой пищи съедает в год средний гражданин республики: известно, сколько в стране охотников, балерин: станков, велосипедов, памятников, маяков и швейных машинок: Как много жизни, полной пыла, страстей и мысли, глядит на нас со статистических таблиц. «.
Это ироничное описание даёт общее представление о статистике.
Термин «статистика» произошел от латинского слова «статус» (status), что означает «состояние и положение вещей».
В процессе беседы учащиеся совместно с учителем приходят к выводу: явления, которые носят массовый характер и подвержены случайной изменчивости, необходимо изучать методами статистики.
Что такое статистика?
Это наука, изучающая количественные показатели развития общества и общественного производства
Роль статистики в нашей жизни настолько значительна, что люди, часто не задумываясь и не осознавая, постоянно используют элементы статистической методологии не только в трудовых процессах, но и в повседневном быту. Работая и отдыхая, делая покупки, знакомясь с другими людьми, принимая какие-то решения, человек пользуется определённой системой имеющихся у него сведений, сложившихся вкусов и привычек, фактов, систематизирует, сопоставляет эти факты, анализирует их, делает выводы и принимает определённые решения, предпринимает конкретные действия. Таким образом, в каждом человеке заложены элементы статистического мышления, представляющего собой способности к анализу и синтезу информации об окружающем нас мире.
Можно без преувеличения сказать, что статистическими методами сегодня пронизана вся наша жизнь.
Как только человеку в его деятельности потребовались количественные характеристики, то есть числа, тут же появилась статистика. Конечно, она не называлась так, но самые первые статистические исследования можно обнаружить и в древних египетских папирусах, и на вавилонских глиняных табличках
Возникновение статистики было связано с потребностями государственного управления. Уже ранние государства — Китай, Египет, Древняя Греция — нуждались в данных о населении и его составе, имущественном положении граждан, количестве скота, земельных угодий и т.д., положивших начало статистической практике. Потребности в статистических данных многократно возросли в период становления и развития капитализма, что стимулировало формирование статистики науки.
Отсутствие строгой, научной базы статистических прогнозов, произвольное толкование статистических данных позволили в конце XIX века английскому премьер — министру Б.Дизраэли заметить: «Есть три вида лжи. Просто ложь, наглая ложь и : статистика».
В XX веке появилась математическая статистика, обладающая универсальными методами сбора, хранения и обработки информации для выработки различных прогнозов.
Одной из основных задач статистики является обработка информации. Конечно, у статистики есть много и других задач: получение и хранение информации, выработка различных прогнозов, оценка их достоверности.
Итак, задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов.
Статистическая информация — это числовые данные о массовых явлениях.
Причины введения курса «Статистика «
Без минимальной вероятностно-статистической грамотности трудно воспринимать социальную, политическую, экономическую информацию и принимать на ее основе обоснованные решения.
Современные физика, химия, биология, весь комплекс социально-экономических наук построен и развиваются на вероятностно-статистической базе.
Без знания понятий и методов теории вероятностей и статистики невозможна организация эффективного конкурентоспособного производства, внедрение новых лекарств и методов лечения в медицине.
Сегодняшний стандарт школьного математического образования ограничивается понятиями и методами описательной статистики, которая занимается первичной обработкой статистической информации:
представлением ее в виде удобно читаемых таблиц, изображением на диаграммах и вычислением наиболее показательных числовых характеристик. Именно эти простейшие методы анализа статистических данных и будут обсуждаться нами
Слайд № 5 ( тема урока)
Элементы математической статистики мы будем изучать на примере нашего класса
При проведении статистического исследования после сбора и группировки данных переходят к их анализу, используя для этого различные обобщающие показатели. Простейшими из них являются среднее арифметическое, мода, медиана, размах.
Статистические характеристики: среднее арифметическое, размах, мода и медиана.
Пример 1. Пусть ученик получил в течение первой учебной четверти следующие отметки по алгебре:
5, 2, 4, 5, 5, 4, 4, 5, 5, 5.
Найдем средний балл, то есть среднее арифметическое всех членов ряда:4,4
Заметьте, что среднее значение ряда может не совпадать ни с одним из его элементов. В примере средний балл получился 4,4. хотя все оценки выражались целыми числами.
Посмотрим еще раз на приведенный ряд. А какую итоговую отметку поставили бы этому ученику вы?
Думаю, что многие ответили бы «5». Можно привести весомый аргумент в пользу такого решения: ведь именно такую отметку ученик получал в течение четверти чаще всего. Такая числовая характеристика называется в статистике модой.
Итак, модой числового ряда называют число, которое встречается в этом ряду наиболее часто. Можно сказать, что оно в этом ряду самое модное, для нашего примера мода равна 5.
В отличие от среднего арифметического. которое можно вычислить для любого числового ряда, моды у ряда может вообще не быть. Например, пусть ученик получил по русскому языку следующие отметки: 4, 2, 3, 5.
Каждая отметка встречается а этом ряду только один раз, и среди них нет числа, встречающегося чаще Значит, у этого ряда нет моды.
Еще одной важной характеристикой числового ряда является его медиана — число ряда, которое делит его ровно пополам. Более точно, медианой числового ряда называют число этого ряда (или полу сумму двух его чисел), слева и справа от которого на
числовой прямой лежит одинаковое количество членов ряда. Чтобы найти медиану числового ряда нужно его сначала упорядочить-составить ранжированный ряд. В нашем примере с отметками он выглядит так:
2, 4, 4, 4, 5, 5, 5, 5, 5, 5.
Если ряд содержит нечетное число членов, то нужно взять число, которое находится ровно посередине.
Если ряд содержит четное число членов (как в нашем примере), то нужно взять два средних числа и найти их полу сумму:
Итак, мы ввели в рассмотрение три числовых характеристики для описания поведения числового ряда:
1. Среднее арифметическое ряда чисел — это частное от деления суммы этих чисел на число слагаемых.
2. Размах ряда чисел — это разность между наибольшим и наименьшим из этих чисел.
3. Модой ряда чисел называется число, наиболее часто встречающееся в данном ряду.
4. Медианой ряда, состоящего из нечётного количества чисел, называется число данного ряда, которое окажется посередине, если этот ряд упорядочить.
Медианой ряда, состоящего из чётного количества чисел, называется среднее арифметическое двух стоящих посередине чисел этого ряда
Рост учащихся нашего класса
157,165,165,168,165,161,165,160,162,169,171, 170,170,175,173,170,177,182,186,182,160,173, 165,162,174,177.
1) составить ранжированный ряд ;
2) определить средний рост, моду ряда, медиану ряда.
157,160,160,161,162,162,165,165, 165,165,165,168,169,170,170,170, 171,173,173,174,175,177,177,182, 186.
Средний рост 168,96 см
Мода ряда (наиболее часто встречающийся рост):165 см
Медиана ряда: 169 см
(у 12 учащихся рост меньше 169см, у 12 учащихся рост больше169см)
Слайд №13 Устная работа
Наглядное представление статистической информации. Примеры (результаты анкеты № 1) приложение №2
Обработка данных анкетирования (анкета № 2) приложение №2 , которое проведено за день до урока.
Создание электронных диаграмм.
Просмотр диаграмм слайды № 21-30
Подводя итоги, хотелось бы сказать, что статистическое наблюдение — интересная и занимательная область математики. Статистические наблюдения используются практически везде, где только можно обусловить их применение. Вместе с тем, несмотря на обширную область применения, статистические наблюдения являются довольно-таки сложным предметом и ошибки нередки. Однако, в целом наблюдения как предмет для рассмотрения представляют собой большой интерес.
1) стр 61 — 82 читать;
2) Практическое задание:
Зная свои оценки за три четверти, составить ранжированный ряд и определить среднее арифметическое, моду ряда, медиану ряда
Источник
Способы наглядного представления статистических данных
4.2. Графическое представление статистических данных
Важное место в современном статистическом анализе социально-экономических явлений и процессов занимает графический метод. Без графиков не обходится ни одно статистическое исследование — они позволяют с наименьшими временными затратами выявить закономерности в развитии явления и его структуру, а также наглядно представить взаимосвязи показателей. Графический образ часто более нагляден и понятен, чем многие страницы текста. Арсенал используемых в статистике графиков обширен. Более того, с появлением новых программных средств он непрерывно увеличивается: на замену плоскостным графикам приходят объемные, матричные, категоризованные графики и пиктографики.
График — это схематичное изображение статистической информации с помощью различных геометрических образов, которыми могут быть линии, точки, плоскостные либо объемные фигуры (круги, прямоугольники и т.д.), символы со многими элементами (звезды, лучи, многоугольники, «лица Чернова», «японские свечи», «ящики с усами» и т.д.).
Любой статистический график содержит графический образ и вспомогательные элементы. Под графическим образом понимают совокупность выбранных для изображения конкретной статистической информации линий, фигур, точек или символов, имеющих определенный формат изображения. Вспомогательные элементы графика — это, во-первых, поле графика ( пространство , на котором располагается геометрический образ, при этом длина и ширина поля графика , как правило, имеют между собой определенное соотношение), во-вторых, система координат и масштабные ориентиры (декартовы, полярные координаты , контурные линии или сетки с нанесенной на них масштабной шкалой), и, в-третьих, экспликация графика , которая представляет собой необходимый разъяснительный текст, прилагаемый к графику: его название, подписи масштабных шкал, смысловое содержание применяемых символов и знаков (легенда графика ).
Статистические графики можно классифицировать по следующим признакам:
- аналитическое предназначение;
- способ построения;
- символы геометрического образа.
По аналитическому предназначению различают графики сравнения, структуры, динамики, изображения вариационных рядов, графики взаимосвязи показателей.
По способу построения графики делятся на диаграммы и статистические карты.
Согласно используемым символам геометрического образа графики бывают точечные, линейные, фигурные (плоскостные или объемные) и пиктографики.
Для сравнения одноименных показателей, относящихся к различным временным периодам, объектам или территориям, применяют линейные графики и различные виды диаграмм: столбиковую, ленточную, фигурную; а также пиктографики.
У линейного графика по оси абсцисс отмечаются временные периоды, объекты или территории, а по оси ординат — соответствующие им значения рассматриваемого показателя. Например, по данным табл. 4.10 построим линейный график изменения удельного веса убыточных организаций за период 2002-2006 гг. для экономики в целом (рис. 4.1).
| Отрасль экономики | Год | ||||
|---|---|---|---|---|---|
| 2002 | 2003 | 2004 | 2005 | 2006 | |
| Всего в экономике, в том числе: | 53,2 | 40,8 | 39,8 | 37,9 | 43,5 |
| промышленность | 48,8 | 39,1 | 39,7 | 39,3 | 45,1 |
| сельское хозяйство | 84,4 | 52,7 | 50,7 | 46,3 | 55,6 |
| строительство | 40,6 | 37,7 | 37,2 | 35,4 | 38,6 |
| транспорт | 53,4 | 47,9 | 44,1 | 40,9 | 45,6 |
| связь | 44,3 | 28,4 | 26,1 | 25,4 | 35,1 |
| торговля и общественное питание | 45,3 | 32,7 | 31,4 | 27,7 | 31,2 |
Столбиковая диаграмма несет тот же аналитический смысл, что и линейный график . При ее построении на оси X располагаются элементы, подлежащие сравнению, которыми могут быть временные периоды, территории, либо объекты. Они находятся на одинаковом расстоянии друг от друга. Затем рисуются прямоугольники (столбики): сторона, являющаяся шириной, одинакова для всех сравниваемых элементов и располагается на оси X, высота прямоугольников откладывается по оси Y пропорционально значению сравниваемого показателя. Таким образом, ось Y должна иметь определенную масштабную шкалу, обязательно начинающуюся с нуля. Так, используя данные табл. 4.10, построим столбиковую диаграмму изменения удельного веса убыточных предприятий и организаций по всей экономике в целом (рис. 4.2).
Прямоугольники столбиковой диаграммы могут располагаться и вплотную друг к другу — расстояние между ними определяется произвольно, масштаб имеет лишь высота прямоугольников.
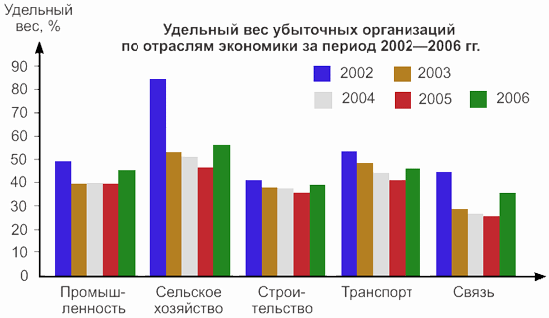
Столбиковые диаграммы могут одновременно демонстрировать изменение нескольких показателей. Для примера изобразим динамику удельного веса убыточных предприятий и организаций по отраслям экономики за несколько временных периодов (рис. 4.3).
Для четырех отраслей построим линейный график (рис. 4.4).
Ленточная (полосовая) диаграмма строится по тем же правилам, что и столбиковая, но прямоугольники, изображающие размеры показателя, располагаются не вертикально, а горизонтально. Данный вид диаграммы удобно применять в тех случаях, когда сравниваемые показатели могут принимать отрицательные значения. Например, магазин детской одежды «Сашенька» в течение года имел не только прибыль (+), но и нес убытки (рис. 4.5).
Для получения диаграмм сравнения могут использоваться и различные геометрические фигуры. Предположим, что количество заключенных договоров личного страхования, заключенных страховой компанией, составляло в 2003 г. 23 тыс., в 2004 г. — 64 тыс. Изобразим эти данные графически, для чего выберем в качестве фигурного знака квадрат. Чтобы найти стороны квадратов нужно извлечь квадратные корни из значений показателей: 
Вместо квадратов часто используются круги. Тогда изображаемые величины должны быть пропорциональны площади круга. Наглядность данного вида диаграмм тем больше, чем сильнее различаются между собой сравниваемые показатели. Действительно, если различия небольшие, то подобный график теряет свой смысл.
В динамических сравнениях, особенно если приводятся данные по месяцам года и в них присутствуют так называемые сезонные колебания, используются радиальные диаграммы. Для этого вычерчивается круг такого радиуса, чтобы при нанесении на него масштабной шкалы верхнее значение шкалы соответствовало наибольшему значению показателя. Затем весь круг делится на 12 частей (если мы рассматриваем помесячные данные) и проставляются номера либо названия месяцев около каждого радиуса. После этого на них откладываются в принятом масштабе значения показателей соответствующих месяцев, и полученные точки соединяются отрезками — образуется замкнутая ломаная линия. Пример построения радиальной диаграммы приведен на рис. 4.7.
Для изображения структуры явления используются прямоугольные или секторные диаграммы.
Продемонстрируем построение круговой секторной диаграммы на данных табл. 4.11.
| Вид основных фондов | Удельный вес инвестиций в их общем объеме, % |
|---|---|
| Жилища | 12,8 |
| Здания (кроме жилых) и сооружения | 41,9 |
| Машины, оборудование, транспортные средства | 38,9 |
| Прочие виды основных фондов | 6,4 |
Для того чтобы построить секторную диаграмму, необходимо определить величину углов секторов: 100% соответствует 360°, тогда 1% равен 3,6°. Пересчитаем наши данные:
- жилища: 12,8 * 3,6 = 46°;
- здания (кроме жилых) и сооружения: 41,9 * 3,6 = 151°;
- машины, оборудование, транспортные средства: 38,9 * 3,6 = 140°;
- прочие виды основных фондов: 6,4 * 3,6 = 23°.
Начертим круг произвольного радиуса и разделим его на четыре соответствующих сектора (рис. 4.8).
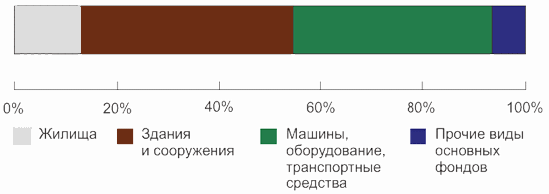
Изобразить графически структуру явления можно также с помощью ленточных (полосовых) диаграмм. В этом случае вычерчивается прямоугольник произвольной длины и ширины. Значение его длины принимается за 100%. Затем прямоугольник делится на части, соответствующие значениям долей тех компонент , из которых состоит явление. Так, по данным табл. 4.10 получим полосовую диаграмму, представленную на рис. 4.9.
Для одновременного изображения трех величин, одна из которых является произведением двух других, применяется особый график , называемый знаком Варзара. Поясним процедуру его построения на условном примере.
Знак Варзара имеет вид прямоугольника, длина и ширина которого соответствуют двум множителям произведения, а площадь — значению произведения, т.д. третьей величине. Так, в табл. 4.12 показатель «Капитализация» рассчитан как произведение рыночной стоимости акции на количество акций данного вида:
| Тип акции | Количество акций, находящихся в обращении, тыс. шт. | Рыночная стоимость акции, ден. ед. | Капитализация, тыс. ден. ед. |
|---|---|---|---|
| А | 70 | 18 | 12 492 |
| Б | 23 | 25 | 575 |
Основание прямоугольников примем за показатель количества, а высоту — за цену. Тогда площадь полученных прямоугольников будет изображать капитализацию. При построении знаков Варзара следует помнить, что основание и высота прямоугольников откладываются в своем масштабе независимо друг от друга (рис. 4.10).
Особое место в графическом анализе финансовой информации занимают биржевые статистические графики.
Для анализа данных фондовых, товарных и фьючерсных рынков чаще всего используют столбиковые биржевые графики (табл. 4.13).
| Дата торгов | Цена открытия | Максимальная цена дня | Минимальная цена дня | Цена закрытия | Объем торгов |
|---|---|---|---|---|---|
| 26 | 14,3 | 14,9 | 14,3 | 14,7 | 102 548 |
| 27 | 14,7 | 15,2 | 14,6 | 14,9 | 112 054 |
| 28 | 14,9 | 15,5 | 14,5 | 15,3 | 136 250 |
| 29 | 15,3 | 16,1 | 14,9 | 15,1 | 108 914 |
| 30 | 15,1 | 15,8 | 14,7 | 15,6 | 103 145 |
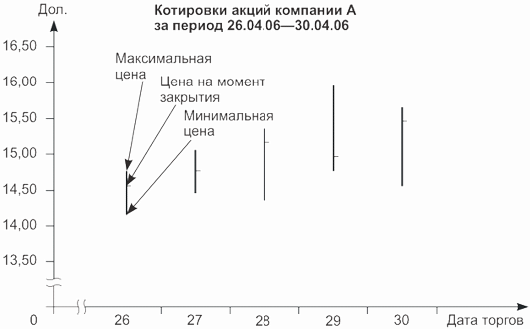
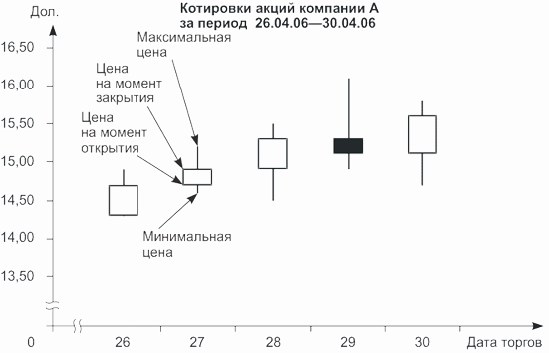
По данным табл. 4.13 построим столбиковый биржевой график (рис. 4.11).
На столбиковом биржевом графике для каждого дня строится вертикальная черта (столбик): начало столбика соответствует значению минимальной в течение дня цены на акцию, вершина — максимальной цене, горизонтальная черта на столбике — цена в момент закрытия торгов.
Для одновременного изображения цен открытия и закрытия торгов, а также минимального и максимального значений цены служит график , часто называемый в литературе «ящики с усами». Для данных табл. 4.13 он выглядит так, как показано на рис. 4.12.
Здесь, в отличие от графика , приведенного на рис. 4.11, у каждого столбика имеется еще и «ящик» (отсюда и название — «ящики с усами»). Основание белого «ящика» соответствует цене открытия торгов, высота — цене закрытия; черный цвет «ящика» означает, что цена закрытия была ниже цены открытия торгов — в этом случае на графике они меняются местами.
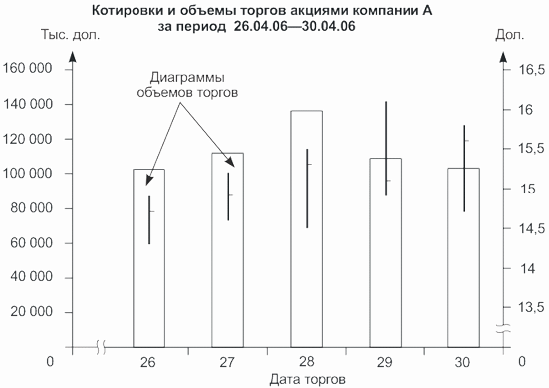
Столбиковый график можно дополнить диаграммами показателя объема торгов. Для данных табл. 4.13 получим графический образ, представленный на рис. 4.13.
Поскольку график дополняется диаграммами, показывающими объемы торгов, то он имеет две вертикальные масштабные шкалы: слева находится шкала для показателя объема торгов, справа — для котировок акций.
График «ящики с усами» также можно дополнить диаграммами показателя объема торгов (рис. 4.14).
В современных статистических пакетах прикладных программ для графического представления статистической информации предлагается особый вид графиков — пиктографики.
Пиктографики составляются для каждого наблюдения, они имеют вид графических объектов (определенных символов) со многими элементами. Значения показателей соответствуют свойствам или размерам элементов пиктографика. С изменением значений показателей при переходе от одной единицы наблюдения к другой внешний вид пиктограммы меняется. Таким образом возникает возможность визуально классифицировать наблюдения по однородным группам.
Предположим, что имеется совокупность 10 промышленных предприятий, характеризующихся следующими показателями (табл. 4.14).
| Номер предприятия | Рентабельность, % | Удельный вес рабочих в составе промышленного производственного персонала, % | Коэффициент сменности оборудования | Удельный вес потерь от брака, % | Фондоотдача на 1 руб. фондов | Среднегодовая численность промышленного производственного персонала, чел. | Среднегодовая стоимость основных производственных фондов, млн. руб. | Оборачиваемость нормируемых оборотных средств, дн. | Оборачиваемость ненормируемых оборотных средств, дн. | Непроизводственные расходы, млн. руб. |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 13,28 | 0,80 | 1,14 | 0,27 | 1,07 | 1 257 | 50,79 | 80,12 | 22,46 | 18,20 |
| 2 | 22,31 | 0,80 | 1,85 | 0,38 | 2,45 | 1 687 | 58,12 | 80,12 | 22,37 | 38,45 |
| 3 | 15,27 | 0,78 | 1,14 | 0,26 | 1,14 | 1 588 | 44,20 | 80,45 | 21,74 | 22,13 |
| 4 | 12,99 | 0,79 | 1,33 | 0,28 | 1,05 | 1 696 | 44,57 | 68,17 | 20,11 | 24,56 |
| 5 | 25,78 | 0,78 | 1,74 | 0,29 | 2,12 | 1 804 | 51,43 | 70,82 | 20,37 | 46,75 |
| 6 | 28,47 | 0,79 | 1,90 | 0,30 | 2,09 | 1 512 | 53,96 | 73,47 | 21,38 | 38,16 |
| 7 | 12,97 | 0,80 | 1,16 | 0,35 | 1,03 | 1 499 | 57,58 | 76,12 | 21,52 | 24,58 |
| 8 | 23,47 | 0,81 | 1,86 | 0,32 | 2,11 | 1 403 | 65,34 | 78,77 | 23,58 | 41,78 |
| 9 | 10,47 | 0,81 | 1,17 | 0,33 | 0,87 | 1 451 | 59,34 | 81,42 | 22,47 | 22,79 |
| 10 | 13,58 | 0,82 | 1,23 | 0,32 | 0,97 | 1 327 | 57,83 | 84,07 | 23,17 | 22,47 |
Проанализируем имеющуюся информацию графически с помощью пиктографиков.
Пиктографики «лучи» имеют вид «велосипедного колеса», в котором количество «спиц» соответствует количеству переменных. Каждая спица — числовая ось , на которой откладывается значение показателя в своем масштабе независимо от масштаба других показателей, причем шкалы начинаются не с нулевого значения, а с наименьшего в данном числовом массиве. Цель пиктографика — продемонстрировать различия в значениях аналогичных показателей у разных единиц наблюдения.
По данным табл. 4.14 построим пиктографики «лучи» (рис. 4.14а).
Как видим, на рис. 4.14а пиктографиков столько, сколько имеется наблюдений. Число лучей каждого пиктографика равно количеству показателей, которые располагаются друг за другом по часовой стрелке, начиная с первого, который находится на верхнем луче, соответствующем 12 часам, если проводить аналогию с часовым механизмом.
Итак, визуальный анализ данных показывает, что сходными по своим экономическим показателям являются предприятия 2 и 8; 5 и 6; 7 и 9.
Преимущество данного способа анализа возрастает с увеличением числа наблюдений, так как при большом их количестве все труднее становится систематизировать полученную информацию, изучая цифры табличным методом.
Другой вид часто применяющихся пиктографиков — «звезды» (рис. 4.14б). Их построение и анализ абсолютно аналогичен пиктографикам «лучи» (у «звезд» лучи не продолжаются за отметками показателей на осях).
Отметим, что в каждом конкретном случае выбор «звезд» или «лучей» — сугубо индивидуальный процесс: кому-то удобнее работать со «звездами», чем с «лучами», а кому-то наоборот.
Следующий, наиболее экзотичный, вид пиктографиков — «лица Чернова» (рис. 4.14в). Здесь для каждого наблюдения рисуется отдельное лицо. Черты лица соответствуют значениям показателей: овал лица — показатель первый, размер ушей — показатель второй, длина носа — показатель третий, форма ушей — показатель четвертый, тип улыбки — показатель пятый, угол наклона бровей — показатель шестой и т.д. Конечно, по данному графику нельзя определить конкретные значения показателей — преследуется вовсе не эта цель, но для классификации наблюдений по однородным группам, выявления взаимосвязей между показателями (если скажем, длина носа меняется с изменением овала лица) «лица Чернова» могут быть полезны.
Источник