Представление чисел в ЭВМ
Целые числа
Для числа +1101 :
| Прямой код | Обратный код | Дополнительный код |
| 0,0001101 | 0,0001101 | 0,0001101 |
Для числа -1101 :
| Прямой код | Обратный код | Дополнительный код |
| 1,0001101 | 1,1110010 | 1,1110011 |
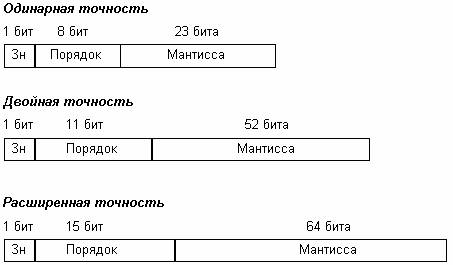
Вещественные числа (числа с плавающей точкой)
Пример .
Запишите код действительного числа, интерпретируя его как величину типа Double.
а) 446,15625;
Переводим десятичное число в двоичное представление.
| Целая часть от деления | Остаток от деления |
| 446 div 2 = 223 | 446 mod 2 = 0 |
| 223 div 2 = 111 | 223 mod 2 = 1 |
| 111 div 2 = 55 | 111 mod 2 = 1 |
| 55 div 2 = 27 | 55 mod 2 = 1 |
| 27 div 2 = 13 | 27 mod 2 = 1 |
| 13 div 2 = 6 | 13 mod 2 = 1 |
| 6 div 2 = 3 | 6 mod 2 = 0 |
| 3 div 2 = 1 | 3 mod 2 = 1 |
| 1 div 2 = 0 | 1 mod 2 = 1 |
Остаток от деления записываем в обратном порядке. Получаем число в 2-ой системе счисления: 110111110
446 = 1101111102
Для перевода дробной части числа последовательно умножаем дробную часть на основание 2. В результате каждый раз записываем целую часть произведения.
0.15625*2 = 0.313 (целая часть 0)
0.313*2 = 0.626 (целая часть 0)
0.626*2 = 1.252 (целая часть 1)
0.252*2 = 0.504 (целая часть 0)
0.504*2 = 1.008 (целая часть 1)
Получаем число в 2-ой системе счисления: 00101
0.15625 = 001012
446.15625 = 110111110,001012 = 1,1011111000101*2 8
Знак S = 0
Порядок P = 8 + 1023 = 103110 = 100000001112
Мантисса: 1011111000101
Для числа с двойной точностью мантисса занимает 52 разряда. Добавляем нули.
Мантисса: 1011 1110 0010 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000
Запишем число:
0 10000000111 1011 1110 0010 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000
В шестнадцатеричной системе счисления: 407BE2800000000016
б) -455,375.
Переводим десятичное число в двоичное представление.
| Целая часть от деления | Остаток от деления |
| 455 div 2 = 227 | 455 mod 2 = 1 |
| 227 div 2 = 113 | 227 mod 2 = 1 |
| 113 div 2 = 56 | 113 mod 2 = 1 |
| 56 div 2 = 28 | 56 mod 2 = 0 |
| 28 div 2 = 14 | 28 mod 2 = 0 |
| 14 div 2 = 7 | 14 mod 2 = 0 |
| 7 div 2 = 3 | 7 mod 2 = 1 |
| 3 div 2 = 1 | 3 mod 2 = 1 |
| 1 div 2 = 0 | 1 mod 2 = 1 |
Остаток от деления записываем в обратном порядке. Получаем число в 2-ой системе счисления: 111000111
455 = 1110001112
Для перевода дробной части числа последовательно умножаем дробную часть на основание 2. В результате каждый раз записываем целую часть произведения.
0.375*2 = 0.75 (целая часть 0)
0.75*2 = 1.5 (целая часть 1)
0.5*2 = 1 (целая часть 1)
0*2 = 0 (целая часть 0)
Получаем число в 2-ой системе счисления: 0110
0.375 = 01102
455,375 = 111000111,01102 = 1,110001110110*2 8 2
Знак S = 1
Порядок P = 8 + 1023 = 103110 = 100000001112
Мантисса: 1100 0111 0110 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000
Запишем число:
1 10000000111 1100 0111 0110 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000
В шестнадцатеричной системе счисления: -455,375 = C07C76000000000016
Дан код величины типа Double. Преобразуйте его число.
а) 408B894000000000;
Представим в двоичном коде:
010000001000 1011 1000 1001 0100 0000 0000 0000 0000 0000 0000 0000 0000 0000
где
S = 0 (положительное число)
P = 100000010002 = 1032 – 1023 = 9
M = 10111000100101
N = 1,10111000100101
С учетом P = 9, N = 1101110001,00101
1101110001 = 2 9 *1 + 2 8 *1 + 2 7 *0 + 2 6 *1 + 2 5 *1 + 2 4 *1 + 2 3 *0 + 2 2 *0+ 2 1 *0 + 2 0 *1 = 512 + 256 + 0 + 64 + 32 + 16 + 0 + 0 + 0 + 1 = 881
Для перевода дробной части необходимо разделить разряд числа на соответствующую ему степень разряда
00101 = 2 -1 *0 + 2 -2 *0 + 2 -3 *1 + 2 -4 *0 + 2 -5 *1 = 0.15625
б) C089930000000000.
Представим в двоичном коде:
1 10000001000 100110010011000000000000000000000000 0000 0000 0000 0000
где
S = 1 (отрицательное число)
P = 100000010002 = 1032 – 1023 = 9
M = 100110010011
N =1,100110010011
С учетом P = 9, N = 1100110010,011
1100110010 = 2 9 *1 + 2 8 *1 + 2 7 *0 + 2 6 *0 + 2 5 *1 + 2 4 *1 + 2 3 *0 + 2 2 *0 + 2 1 *1 + 2 0 *0 = 512 + 256 + 0 + 0 + 32 + 16 + 0 + 0 + 2 + 0 = 818
Для перевода дробной части необходимо разделить разряд числа на соответствующую ему степень разряда
011 = 2 -1 *0 + 2 -2 *1 + 2 -3 *1 = 0.375
Источник
Двоичная система счисления
Двоичная система — это один из видов позиционных систем счисления. Основание данной системы равно двум, то есть используется только два символа для записи чисел.
Немного истории
Впервые о данной системе чисел заговорил основоположник математического анализа Г.В. Лейбниц еще в XVII веке. Он доказал, что для данного множества действуют все арифметические операции: сложение, вычитание, умножение и даже деление. Однако вплоть до 30-х годов XX века данную систему не рассматривали всерьез. Но с развитием электронных устройств и ЭВМ, ученые вновь принялись к изучению данной темы, так как двоичная система отлично подходила для программирования и организации хранения данных в памяти компьютеров.
Таблица и алфавит
Алфавит двоичной системы счисления состоит всего из двух знаков: 0 и 1 . Однако это нисколько не усложняет выполнение арифметических действий.
Кроме того, двоичная система является самой удобной для быстрого перевода в другие системы счисления.
Так, чтобы перевести двоичное число в десятичное, необходимо найти значение его развернутой формы . Например:
1001102 = 1 ∙ 2 5 + 0 ∙ 2 4 + 0 ∙ 2 3 + 1 ∙ 2 2 + 1 ∙ 2 2 + 0 ∙ 2 0 = 32 + 0 + 0 + 4 + 2 + 0 = 3810
Чтобы наоборот перевести число в двоичную из десятичной, необходимо выполнить его деление на 2 с остатком, а затем записать все остатки в обратном порядке, начиная с частного:
| Делимое | 38 | 19 | 9 | 4 | 2 |
|---|---|---|---|---|---|
| Делитель | 2 | 2 | 2 | 2 | 2 |
| Частное | 19 | 9 | 4 | 2 | 1 |
| Остаток | 0 | 1 | 1 | 0 | 0 |
Для перевода в другие системы необходимо:
- Перевести двоичный код в десятичный.
- Выполнить деление десятичного числа на основание той системы, в которую требуется перевести.
Однако можно воспользоваться и более быстрым и удобным способом: разделить знаки двоичного числа на условные группы слева на право (для восьмеричной — по 3 знака; для шестнадцатеричной — по 4 знака), а затем воспользоваться таблицей перевода:
| Двоичная | Восьмеричная | Шестнадцатеричная |
|---|---|---|
| 0 | 0 | 0 |
| 001 | 1 | 1 |
| 010 | 2 | 2 |
| 011 | 3 | 3 |
| 100 | 4 | 4 |
| 101 | 5 | 5 |
| 110 | 6 | 6 |
| 111 | 7 | 7 |
| 1000 | 8 | |
| 1001 | 9 | |
| 1010 | A | |
| 1011 | B | |
| 1100 | C | |
| 1101 | D | |
| 1110 | E | |
| 1111 | F |
110010012 = 11 001 001 = 011 001 001 = 3118
110010012 = 1100 1001 = С916
Представление двоичных чисел
В двоичной системе также существует понятие «отрицательных» чисел. И для того, чтобы провести какую-либо операцию с ними в двоичном коде, необходимо представить его в виде дополнительного кода. Запись положительного числа при этом не меняется ни для одного из кодов.
Чтобы найти дополнительный код отрицательного числа, необходимо воспользоваться его прямым и дополнительным кодами.
Прямой код предполагает приписывание единицы в начале без изменений записи:
| A > 0 | Aпр = 0A | 1010112; Aпр = 01010112 |
| A ≤ 0 | Aпр = 1|A| | -1010112; Aпр = 11010112 |
Для записи обратного кода цифры заменяют на противоположное значение, первую единицу от прямого кода оставляют без изменений:
| A > 0 | Aобр = 0A | 1010112; Aобр = 01010112 |
| A ≤ 0 | Aобр = 1 A | -1010112; Aобр = 10101002 |
Дополнительный код предполагает использование обратного кода, с той лишь разницей, что к отрицательному числу прибавляют единицу:
| A > 0 | Aдоп = 0A | 1010112; Aдоп = 01010112 |
| A ≤ 0 | Aдоп = 1 A + 1 | -1010112; Aдоп = 10101012 |
Применение двоичной системы в информатике
Двоичная система получила особое распространение в программировании цифровых устройств, так как она соответствует требованиям многих технических устройств, поддерживающих два состояния (есть ток, нет тока). Кроме того, является более простой и надежной для кодирования информации. Именно поэтому программный код большей части ЭВМ основан именно на двоичной системе счисления.
Источник