Способы представлений логических операций

Логические операции и их свойства

Вы будете перенаправлены на Автор24

Конъюнкция или логическое умножение (в теории множеств – это пересечение)

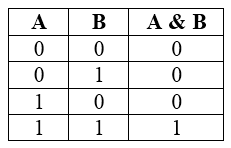
Конъюнкция является сложным логическим выражением, которое истинно в том и только том случае, когда оба простых выражения являются истинными. Такая ситуация возможно лишь в единственном случае, во всех остальных случаях конъюнкция ложна.

Обозначение: &, $\wedge$, $\cdot$.

Таблица истинности для конъюнкции

1. Если хотя бы одно из подвыражений конъюнкции ложно на некотором наборе значений переменных, то и вся конъюнкция будет ложной для этого набора значений.
2. Если все выражения конъюнкции истинны на некотором наборе значений переменных, то и вся конъюнкция тоже будет истинна.
3. Значение всей конъюнкции сложного выражения не зависит от порядка записи подвыражений, к которым она применяется (как в математике умножение).

Дизъюнкция или логическое сложение (в теории множеств это объединение)

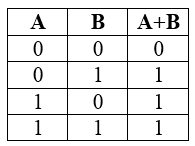
Дизъюнкция является сложным логическим выражением, которое истинно практически всегда, за исключением, когда все выражения ложны.

Таблица истинности для дизъюнкции

1. Если хотя бы одно из подвыражений дизъюнкции истинно на некотором наборе значений переменных, то и вся дизъюнкция принимает истинное значение для данного набора подвыражений.
2. Если все выражения из некоторого списка дизъюнкции ложны на некотором наборе значений переменных, то и вся дизъюнкция этих выражений тоже ложна.
3. Значение всей дизъюнкции не зависит от порядка записи подвыражений (как в математике – сложение).

Готовые работы на аналогичную тему

Отрицание, логическое отрицание или инверсия (в теории множеств это отрицание)

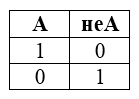
Отрицание — означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО и в итоге получаем, что если исходное выражение истинно, то отрицание исходного – будет ложно и наоборот, если исходное выражение ложно, то его отрицание будет истинно.

Обозначения: не $A$, $\bar$, $¬A$.

Таблица истинности для инверсии

«Двойное отрицание» $¬¬A$ является следствием суждения $A$, то есть имеет место тавтология в формальной логике и равно самому значению в булевой логике.

Импликация или логическое следование

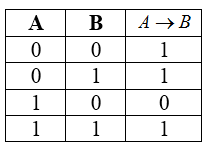
Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть, данная логическая операция связывает два простых логических выражения, из которых первое является условием ($A$), а второе ($A$) является следствием условия ($A$).

Обозначения: $\to$, $\Rightarrow$.

Таблица истинности для импликации

1. $A \to B = ¬A \vee B$.
2. Импликация $A \to B$ ложна, если $A=1$ и $B=0$.
3. Если $A=0$, то импликация $A \to B$ истинна при любом значении $B$, (из лжи может следовать истинна).

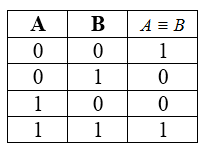
Эквивалентность или логическая равнозначность

Эквивалентность — это сложное логическое выражение, которое истинно на равных значениях переменных $A$ и $B$.

Обозначения: $\leftrightarrow$, $\Leftrightarrow$, $\equiv$.

Таблица истинности для эквивалентности

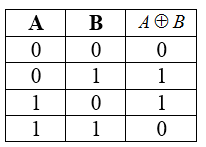
Строгая дизъюнкция или сложение по модулю 2 ( в теории множеств это объединение двух множеств без их пересечения)

Строгая дизъюнкция истинна, если значения аргументов не равны.

Для функции трёх и более переменных результат выполнения операции будет истинным только тогда, когда количество аргументов равных $1$, составляющих текущий набор — нечетное. Такая операция естественным образом возникает в кольце вычетов по модулю 2, откуда и происходит название операции.

Обозначения: $A \oplus B$ (в языках программирования), $A≠B$, $A \wedge B$ (в языках программирования).

Таблица истинности для операции сложения по модулю два

Свойства строгой дизъюнкции:

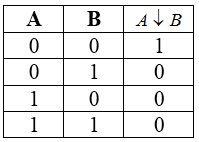
Стрелка Пирса

Бинарная логическая операция, булева функция над двумя переменными. Названа в честь Чарльза Пирса и введена в алгебру логики в $1880—1881$ гг.

Обозначения: $\downarrow$ , ИЛИ-НЕ

Таблица истинности для стрелки Пирса

Стрелка Пирса, как и конъюнкция, дизъюнкция, отрицание, образует базис для булевых функций двух переменных. При помощи стрелки Пирса, можно построить все остальные логические операции, например:

$X \downarrow X = ¬X$— отрицание

$(X \downarrow Y) \downarrow (X \downarrow Y) \equiv X \vee Y$ — дизъюнкция

$(X \downarrow X) \downarrow (Y \downarrow Y) \equiv X \wedge Y$ — конъюнкция

$((X \downarrow X) \downarrow Y) \downarrow ((X \downarrow X) \downarrow Y) = X \to Y$ — импликация

В электронике стрелка Пирса представлена в виде элемента, который носит название «операция 2ИЛИ-НЕ» (2-in NОR).

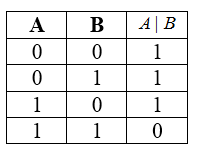
Штрих Шеффера

Булева функция двух переменных или бинарная логическая операция. Введена в рассмотрение Генри Шеффером в 1913 г.

Обозначения: $|$, эквивалентно операции И-НЕ.

Таблицей истинности для функции штрих Шеффера

Штрих Шеффера образует базис для всех булевых функций двух переменных. Применяя штрих Шеффера можно построить остальные операции, например,

$X \mid X = ¬X$ — отрицание

$(X \mid Y) \mid (X \mid Y) = (X \wedge Y)$ — конъюнкция

$(X \mid X) \mid (Y \mid Y) = X \vee Y$ — дизъюнкция

Для электроники это означает, что реализация схем возможна с использованием одного типового элемента (правда это дорогостоящий элемент).

Порядок выполнения логических операций в сложном логическом выражении

1. Инверсия(отрицание);
2. Конъюнкция (логическое умножение);
3. Дизъюнкция и строгая дизъюнкция (логическое сложение);
4. Импликация (следствие);
5. Эквивалентность (тождество).

Для того чтобы изменить указанный порядок выполнения логических операций, необходимо использовать скобки.

Общие свойства

Для набора из $n$ логических переменных существует ровно $2^n$ различных значений. Таблица истинности для логического выражения от $n$ переменных содержит $n+1$ столбец и $2^n$ строк.

Источник

Способы представлений логических операций

2) Логическое сложение или дизъюнкция:

Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженbя ложны.
Обозначение: F = A v B.

Таблица истинности для дизъюнкции

A	B	F
1	1	1
1	0	1
0	1	1
0	0	0

3) Логическое отрицание или инверсия:

Инверсия — это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.

Обозначение: F = ¬ A.

Таблица истинности для инверсии

A	¬ А
1	0
0	1

4) Логическое следование или импликация:

Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.

«A → B» истинно, если из А может следовать B.

Обозначение: F = A → B.

Таблица истинности для импликации

A	B	F
1	1	1
1	0	0
0	1	1
0	0	1

5) Логическая равнозначность или эквивалентность:

Эквивалентность — это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.

Источник

6.3. Способы представления логических функций

Табличный способ представления логической функции.

В данном случае ЛФ представля-

ется своей таблицей истинности .

Например, представление ЛФ трех аргументов f ( x 1 , x 2 , x 3 ) ее таблицей истинности:

Табличный способ является максимально наглядным, но в случае сложных функций алгебры логики (ФАЛ) он недостаточно компактен.

Аналитический (алгебраический) способ представления логической функции

Аналитический (алгебраический) способ представления логической функции – это аналитическая запись функции в виде формулы, по которой можно реализовать логическое устройство, состоящее из логических элементов, каждый из которых реализует элементарную логическую операцию. В результате операции, выполняемой логическим элементом, на его выходе появляется сигнал «да» – 1 или «нет» – 0, таким образом, это действие может быть выражено двоичным кодом.

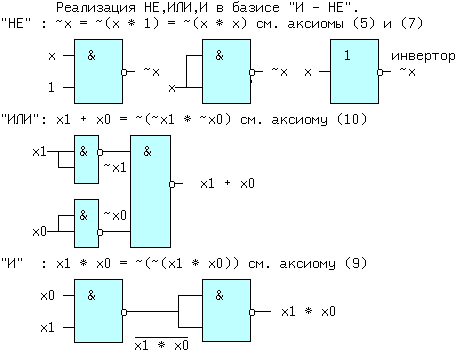
Любая сложная логическая операция может быть разложена на элементарные логические функции – «НЕ» (логическое отрицание), «ИЛИ» (дизъюнкция), «И» (конъюнкция). Например,

f 1 ( x 1 , x 2 , x 3 ) = x 3 + x 1 x 2 + x 2 x 3 + x 1 x 2 x 3

f 2 ( x 1 , x 2 , x 3 ) = ( x 1 + x 2 ) ( x 2 + x 3 ) ( x 1 + x 2 + x 3 )

Макстерм H (дизъюнктивный терм) – это ЛФ, связывающая все переменные в прямой и инверсной форме (литералы) знаком дизъюнкции (например, для f 2 ( x 1 , x 2 , x 3 ) : x 1 + x 2 + x 3 – макстерм

максимального ранга, так как присутствуют все переменные функции). Элементарная сумма – это дизъюнкция нескольких переменных или их отрицаний (например, для f 2 ( x 1 , x 2 , x 3 ): x 1 + x 2 ).

Минтерм F (конъюнктивный терм) – это ЛФ, связывающая все переменные в прямой и инверсной форме (литералы) знаком конъюнкции (например, для f 1 ( x 1 , x 2 , x 3 ): x 1 x 2 x 3 – минтерм

максимального ранга, так как присутствуют все переменные функции). Элементарное произведение – это конъюнкция нескольких переменных или их отрицаний (например, для f 1 ( x 1 , x 2 , x 3 ):

Нормальные формы аналитического представления ЛФ :

• нормальная дизъюнктивная форма ( НДФ ) – это ∑ F i или F i , где F i – минтермы любого

ранга, включая единичный, ∑ и

– знаки логического сложения;

нормальная конъюнктивная форма ( НКФ ) – это П H i или H i , где H i – макстермы любого

включая единичный, П и

– знаки логического умножения;

совершенная нормальная дизъюнктивная форма ( СНДФ ) – это ∑ F i или

F i , где F i – мин-

термы только максимального ранга;

совершенная нормальная конъюнктивная форма ( СНКФ ) – это П H i или

H i , где H i – мак-

стермы только максимального ранга.

Любая совершенная нормальная форма (СНФ) отличается от нормальной тем, что всегда содержит термы только максималь-ного ранга и дает однозначное представление логической функции.

Любая таблично заданная ФАЛ (ЛФ) может быть пред-ставлена аналитически в виде дизъюнкции конечного числа минтермов, т.е. НДФ и СНДФ. На каждом из минтермов функция равна единице:

f ( x 1 , x 2 . x n ) = F 0 + F 1 + . + F n -1 = ∑ F i = F i ,

i – номера наборов, на которых функция равна единице.

СНДФ функции находится следующим образом: формируется дизъюнкция произведений (минтермов) всех аргументов с количе-ством слагаемых, равным числу наборов, на которых функция равна единице; в каждом минтерме над аргументом, значение которого равно нулю, ставится знак отрицания. Например, записать в аналитической форме функцию, заданную таблично:

Источник

Способы представлений логических операций

1.1 ОСНОВНЫЕ ПОЛОЖЕНИЯ АЛГЕБРЫ ЛОГИКИ

В отличие от аналоговых электронных устройств, в цифровых устройствах (ЦУ) входные и выходные сигналы могут принимать ограниченное количество состояний. В соответствии с логическим соглашением (ГОСТ 2.743-82), в зависимости от конкретной физической реализации элементов ЦУ, более положительному значению физической величины, «H» — уровень, соответствует состояние «логическая 1«, а менее положительному значению ,»L — уровень» — «логический 0«. Такое соглашение называется положительной логикой. Обратное соотношение называется отрицательной логикой. В ГОСТ’е 19480 — 89 даны наименования, определения и условные обозначения основных параметров и характеристик цифровых микросхем.

Теоретической основой проектирования ЦУ является алгебра-логики или булева алгебра, оперирующая логическими переменными. Для логических переменных, принимающих только два значения,существуют 4 основных операции. Операция логическое «И» (AND) конъюнкция или логическое умножение, обозначается * или /\. Операция логическое «ИЛИ» (OR), дизъюнкция или логическое сложение, обозначается + или \/ . Операция логическое «НЕ» (NOT), изменение значения, инверсия или отрицание, обозначается чертой над логическим выражением. Инверсия иногда будет в тексте обозначаться знаком «

«. Операция эквивалентности обозначается «=» . Следующие соотношения являются аксиомами.

(1)	0 + 0 = 0	1 * 1 = 1	(1′)
(2)	1 + 1 = 1	0 * 0 = 0	(2′)
(3)	1 + 0 = 0 + 1 = 1	0 * 1 = 1 * 0 = 0	(3′)
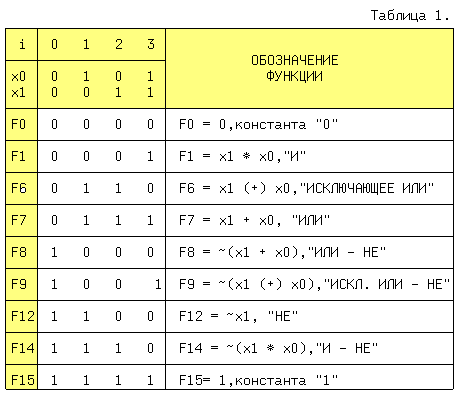
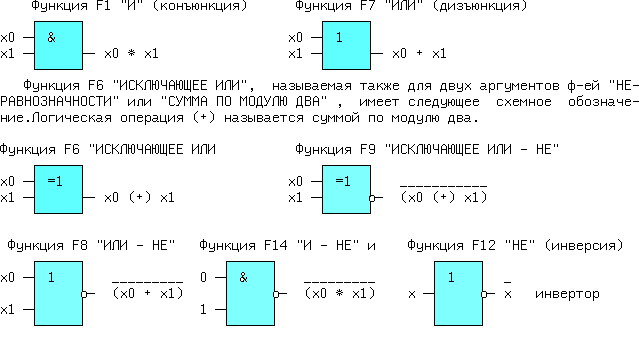
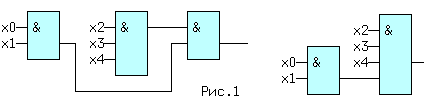
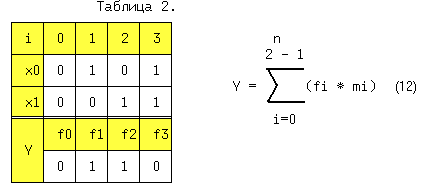
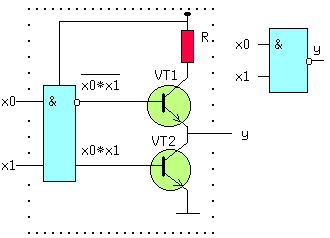
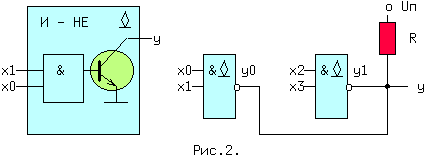
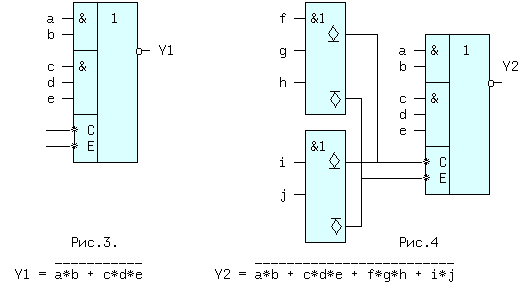
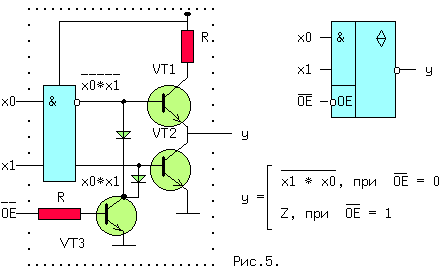
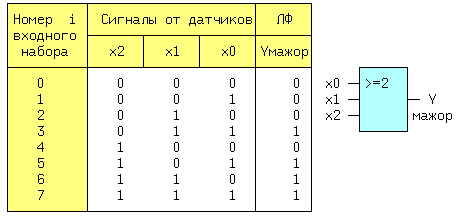
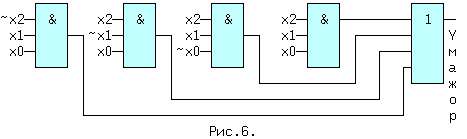
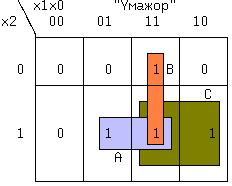
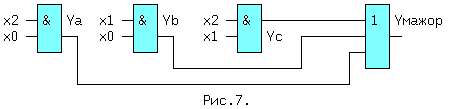
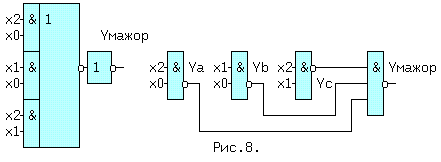
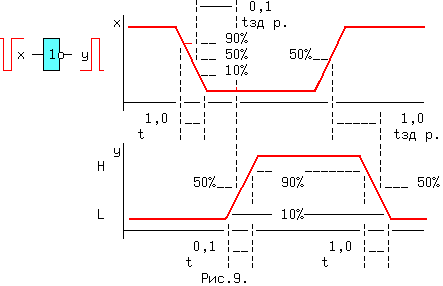
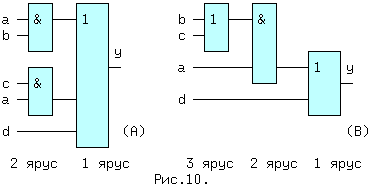
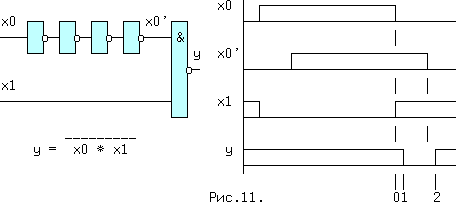
(4)	Из (1, 2) и (1′,2′) следует: x + x = x и x * x = x. (5) Из (1, 3) и (2′,3′) следует: x + 0 = x и 0 * x = 0. (6) Из (2, 3) и (1′,3′) следует: 1 + x = 1 и x * 1 = x. (7) Из (3) и (3′) следует: x + Из (4) и (4′) следует: И, наконец, из (1,1′), (2,2′), (3,3′) и (4,4′) следует: Последние выражения (10) называют принципом двойственности или теоремой Де Моргана (инверсия логической суммы равна логическому произведению инверсий и наоборот). Соотношения двойственности для n переменных, часто записывают в виде: На функции И и ИЛИ распространяются обычные алгебраические законы — переместительный, сочетательный и распределительный, которые легко доказываются методом перебора: x1 op x0 = x0 op x1 — переместительный, x2 op x1 op x0 = (x2 op x1) op x0 — сочетательный и x2*(x1+x0) = (x2*x1) + (x2*x0) и x2 + (x1*x0) = (x2+x1) * (x2+x0) — распределительный, где операция op может быть, либо И, либо ИЛИ. Наряду с тремя основными логическими функциями, называемыми также переключательными, существуют и другие. 1.2 ПЕРЕКЛЮЧАТЕЛЬНЫЕ ФУНКЦИИ Для n — логических переменных (аргументов) существует 2 n их комбинаций или двоичных наборов. На каждом таком наборе может быть определено значение функции 0 или 1. Если значения функции отличаются хотя бы на одном наборе, функции — разные. Общее число переключательных функций (ПФ) от n аргументов равно N=2 2 n . Для n=2, N=16. При n=3, N=256 и далее очень быстро растет. Практическое значение имеют 16 функций от 2-х переменных, т.к. любое сложное выражение можно рассматривать как композицию из простейших. В таблице 1 приведены некоторые из ПФ для n=2. i-номер набора входных переменных x1 и x0. ЗАПОМНИТЕ СЛЕДУЮЩИЕ ОПРЕДЕЛЕНИЯ. Функция «И» равна единице, если равны единице ВСЕ ее аргументы. Функция «ИЛИ» равна единице, если равен единице ХОТЯ БЫ один аргумент. Функция «ИСКЛЮЧАЮЩЕЕ ИЛИ» (XOR) равна единице, если равен единице ТОЛЬКО один ее аргумент. 1.3 УСЛОВНЫЕ ОБОЗНАЧЕНИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ НА СХЕМАХ Количество входов логического элемента, участвующих в формировании логической функции, называется коэффициентом объединения — Коб ( не путать с коэффициентом разветвления). У всех выше приведенных схем, за исключением инвертора, коэффициент объединения равен двум. Промышленностью выпускаются схемы с Коб=2,3,4,8. Для получения схем с другим числом входов основные элементы можно объединять. Например, если требуется пятивходовая схема И, то ее можно получить, используя сочетательный закон следующим способом: x0 * x1 * x2 * x3 * x4 = (x0*x1) * (x2*x3*x4) = (x0*x1) * x2 * x3 * x4, т.е. требуются две двухвходовые и одна трехвходовая схемы И, для первого варианта, либо одна двухвходовая и одна четырехвходовая — для второго (рис.1). Можно использовать и восьмивходовую схему И, подав на незадействованные входы «1», либо некоторые из переменных, в соответствии с выражениями (5) или (7). 1.4 СПОСОБЫ ПРЕДСТАВЛЕНИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ Целью проектирования цифрового устройства является получение его логической функции (ЛФ) и соответствующей ей схемной реализации. ЛФ могут иметь различные формы представления: 1) словесное, 2) графическое, 3) табличное, 4) алгебраическое, 5) на алгоритмическом языке (например VHDL) и 6) схемное. В качестве примера, рассмотрим функцию Y от двух переменных x1 и x0, заданную словесным описанием: Y=1, если переменные НЕ РАВНЫ и Y=0, если x1=x0. Такую ЛФ удобно назвать функцией НЕРАВНОЗНАЧНОСТИ. Переходим к табличному представлению Y (таблица 2). Табличное представление значений ЛФ для всех наборов входных переменных называется таблицей истинности. В общем виде переход от табличного представления к алгебраическому может осуществляться по формуле (12), одной из основных в алгебре логики. Выражение (12) называется совершенной дизъюнктивной нормальной формой ЛФ (СДНФ). mi — минтерм или логическое произведение всех переменных i-го двоичного набора, входящих в прямом виде, если значение этой переменной в наборе равно 1, и в инверсном виде, если ее значение равно 0. fi — значение ЛФ на i — ом наборе. Доказательство (12) базируется на теореме разложения, в соответствии с которой любую ЛФ f(..) от n-переменных можно разложить по переменной xi в виде: f(x(n-1). xi,. . x0) = xi*f(x(n-1). 0. x0) + xi*f(x(n-1). 1. x0). Это выражение для xi=0 равно 0*f(x(n-1). 0. x0) + 0*f(x(n-1). 1. x0) = f(x(n-1). 0. x0). При xi=1 оно будет равно 1*f(x(n-1). 1. x0) + 1*f(x(n-1). 1. x0) = f(x(n-1). 1. x0), т.е. при любых значениях xi теорема разложения справедлива. Теорему разложения можно применить n раз и тогда ЛФ будет разложена по всем своим переменным. В виде примера рассмотрим функцию F=f(x1,x0) от двух переменных. Разложение этой функции по переменной x1 даст: F= x1*f(0,x0) + x1*f(1,x0) . Продолжая эту операцию для переменной x0, получим: Выражение (12.1) позволяет записать все переключательные функции от двух переменных, используя только три основных логических операции. Рассмотрим разложение функций F7-«ИЛИ» и F1-«И», для чего необходимо обратиться к соответствующим строчкам таблицы 1. Функция И на двоичных наборах входных переменных x1 и x0 (00,01,10,11) принимает значения 0,0,0,1. Записывая выражение (12.1) для этих значений получим: F1(x1,x0 ) = x0*0 + x1*x0*1 = x1*x0, что соогласуется с ее определением. Таким же образом, находим алгебраическое выражение функции F7-«ИЛИ», которая, соответственно, на тех же входных наборах принимает значения: 0,1,1,1. Тогда, в соответствии с (12.1), F7(x1,x0) = x0*1 + x1*x0*1. Вынося за скобки в двух последних слагаемых x1, получим F7 = x0*1 + x0*1). На основании аксиомы (8), выражение в скобке равно «1» и F7 = x1*x0*1 + x1. Применяя распределительный закон, найдем ( Возвращаясь к таблице 2, получим Y = 0* x0 = x1 (+) x0 = F6 (функцияия неравнозначности). С помощью формулы (12) любую, сколь угодно сложную, логическую функцию можно представить в виде трех основных ЛФ: «И», «ИЛИ», «НЕ», представляющих собой логический базис. 1.5 ЛОГИЧЕСКИЙ БАЗИС Набор простейших ЛФ, позволяющих реализовать любую другую функцию называется логическим базисом (ЛБ). Функции И, ИЛИ, НЕ не являются минимальным ЛБ, т.к. сами могут быть представлены через другие функции, например через F8(ИЛИ -НЕ) или F14(И — НЕ). Следовательно базис «И — НЕ» является минимальным. Реализацию НЕ,И,ИЛИ в базисе «ИЛИ — НЕ» произвести самостоятельно, используя перечисленные аксиомы. 1.6 СХЕМНЫЕ ОСОБЕННОСТИ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ Приведенные выше логические элементы (ЛЭ) И, ИЛИ, НЕ, И-НЕ и другие могут иметь некоторые схемотехнические особенности. 1.6.1 БАЗОВЫЙ ЛОГИЧЕСКИЙ ЭЛЕМЕНТ На рисунке приведена упрощенная схема И-НЕ и его условное обозначение. Напряжения на базах транзисторов VT1 и VT2 находятся в противофазе и, если x0*x1=1, то нижний транзистор открыт, а верхний закрыт, так как (x0*x1)=0 . Потенциал коллектора VT2 в этом случае примерно равен нулю и следовательно y=0. При других значениях x0 и x1 нижний транзистор закрыт, а верхний открыт и на выходе схемы — высокий уровень, т.е. схема работает как элемент И-НЕ. Выходы нескольких БЛЭ категорически нельзя соединять вместе, потому что, если n-1 элементов находятся в состоянии «1», а n-ый в состоянии «0», то n-1 транзисторов VT1 будут «сливать» (sink) токи в единственный транзистор VT2 n-го элемента. Суммарный ток может превысить допустимое значение и VT2 выйдет из строя. 1.7 ЭЛЕМЕНТ С ОТКРЫТЫМ КОЛЛЕКТОРОМ Логический элемент И-НЕ с открытым коллектором (ОК) (см.рис.2. слева) обозначается в поле элемента ромбом с чертой внизу. К открытому коллектору снаружи могут подключаться резисторы, обмотки реле и двигателей, светодиоды и т.д. Открытые коллекторы нескольких элементов в отличие от базового логического элемента могут соединяться вместе, образуя «монтажное И» (рис.2 — справа) для прямых значений переменных т.к. y=y0*y1=1 при y0=y1=1. Иногда такую схему называют «монтажное ИЛИ«, потому что y = (x0*x1 + x2*x3) (рис.2). Логический элемент И с открытым эмиттером, обозначается ромбом, но с чертой сверху. 1.8 ЭЛЕМЕНТЫ «И — ИЛИ — НЕ» И РАСШИРИТЕЛИ Такие схемы объединяют несколько элементов И, подключенных выходами к элементу ИЛИ-НЕ (рис.3). Если количества переменных a,b. e недостаточно, используются элементы-расширители, подключаемые к входам расширения C и E (входы для открытых коллектора и эмиттера). Символ &1 обозначает функцию И, объединяемую по ИЛИ (рис.4). Здесь и далее символом * обозначаются вспомогательные входы у логических элементов. В этих схемах, как и вообще в элементах ИЛИ, неиспользуемый вход ИЛИ д.б. подключен к 0. Поэтому, если одна из секций И незадействована, на один из ее входов необходимо подать 0. В противном случае Y всегда будет равен 0. Это особенность схем, выполненных по ТТЛ(Ш) технологии, т.к. неподключенный логический вход этих схем эквивалентен логической 1 (правда при этом ухудшаются некоторые характеристики микросхемы). 1.9 ТРИСТАБИЛЬНЫЕ ЭЛЕМЕНТЫ Наряду с двумя логическими состояниями существует третье технологическое состояние, когда выход элемента отключается от внутренней схемы. При этом сопротивление между выходом и «землей» становится очень большим и выход микросхемы не оказывает никакого влияния на подключенные к нему выходы других микросхем. Выходы нескольких таких элементов также могут соединяться вместе. Такое включение , разновидность «монтажного И», применяется там, где несколько источников сигналов по очереди подключаются к входам одного или нескольких приемников, не мешая друг другу. Третье состояние называют также высокоимпедансным или Z — состоянием. Схема И-НЕ с Z-состоянием выхода приведена на рис.5. слева, а ее условное обозначение — справа. OE=0, транзистор VT3 закрыт и включенные встречно диоды не оказывают влияния на логические выходы элемента И. Напряжения на базах транзисторов VT1 и VT2 находятся в противофазе и, если x0*x1=1, то верхний транзистор закрыт, а нижний открыт. Потенциал коллектора VT2 примерно равен нулю и следовательно y=0. При других значениях x0 и x1 нижний транзистор заперт, а верхний открыт и на выходе схемы — высокий уровень, т.е. при OE=0 схема работает как обычный элемент И-НЕ. Картина существенно изменится при OE=1. Транзистор VT3 откроется до насыщения и на базах транзисторов VT1 и VT2 потенциал опустится примерно до нуля, запирая их. Выход «y» окажется отключенным от внутренней логической схемы. На схемах тристабильные элементы обозначаются ромбом с поперечной чертой или буквой Z. Такие элементы используются там, где необходима передача инфориации по одной линии от нескольких источников к одному или нескольким приемникам. Причем, так как линия одна, то чтобы выходы пассивных источников не искажали информацию на выходе активного источника, они должны переводиться в третье состояние. Z — состояние используется по этой причине в микросхемах памяти, шинных формирователях. Дополнительный инверсный вход относится к категории управляющих или функциональных. Функция входа зашифрована в его обозначении (Output Enable — разрешение выхода ( OE)),а значение активного уровня на этом входе,при котором функция выполняется, равно 1, если вход прямой, и равно 0, если вход инверсный , как на схеме. 1.10 МИНИМИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ Полученные по формуле СДНФ (12) выражение может быть преобразовано (не всегда) к виду, имеющему меньшее число переменных и операций по сравнению с исходным. Такое преобразование называется минимизацией. Рассмотрим пример. Имеется три двоичных датчика xi. Необходимо реализовать ЛФ Yмажор принимающую значение 1, когда равны 1 значения двух и более датчиков. Такая функция называется мажоритарной. Ее таблица истинности имеет вид: По формуле (12): Yмажор = x0 + x2*x1*x0. (3,5,6,7 — строчки таблицы ). Полученному выражению соответствует схема на рис.6. Схема содержит 4 трехвходовых элемента «И» и 1 четырехвходовый элемент «ИЛИ». Нахождение минимальной формы ЛФ производится методом алгебраических преобразова- ний, с помощью таблиц Карно или машинными методами для больших проектов. 1.11 ТАБЛИЦА КАРНО Таблица Карно (ТК) это видоизмененная запись таблицы истинности. Для функции мажоритарности из последнего примера (ТК) выглядит следующим образом: Правила построения ТК с ледующие: 1)Количество клеток ТК равно количеству строк таблицы истинности. 2)Слева и сверху располагаются значения аргументов. Порядок размещения аргументов таков, что в двух соседних по горизонтали и вертикали клетках отличается значение только одного аргумента (поэтому соседними считаются и клетки, находящиеся на противоположных краях таблицы). 3)В клетки заносятся соответствующие значения ЛФ. 4)Единичные клетки объединяются в прямоугольники (импликанты) по 2^i клеток. 5)Для каждого прямоугольника записывается произведение тех аргументов, которые в соседних клетках не изменяют своего значения. 6)Переменные входят в произведение в прямом виде, если их значение в соседних клетках равно 1, в противном случае в инверсном. 7)Полученные произведения складываются по ИЛИ в искомую ЛФ. В примере имеется 3 прямоугольника — A,B,C, причем Ya = x2*x0 (x1 в соседних клетках меняет свое значение, поэтому в конъюнкцию не входит). Yb = x1*x0 и Yс = x2*x1. Yмажор = Ya + Yb + Yc = x2*x0 + x1*x0 + x2*x1. (13) Соответствующая схема (рис.7.) проще, чем на рис.6. 1.12 ПРЕОБРАЗОВАНИЕ ЛФ К БАЗИСУ «И-НЕ» И «И-ИЛИ-НЕ» Применяя к выражению (13) аксиому двойного отрицания (9) получим: ( x2*x0 + x1*x0 + x2*x1)) (14) Формуле (14) соответствует схема (рис.8,слева) в базисе И-ИЛИ-НЕ. Применяя к выражению (14) соотношение двойственности (11) получим (x2*x1)) . Последнему выражению соответствует схема в базисе И-НЕ (рис.8, справа). 1.13 ВРЕМЕННЫЕ ПАРАМЕРЫ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ Рассмотрим реакцию инвертора на изменение входного сигнала (рис.9). Инерционные свойства инвертора приводят к задержке сигнала при его прохождении от входа к выходу. Процесс изменения напряжения от низкого уровня L к высокому H, называется фронтом сигнала (положительным перепадом, положительным фронтом), а обратный процесс — спадом (отрицательным перепадом, отрицательным фронтом). Если существенно их взаимное расположение, то фронт может быть передним и задним. Длительность фронтов на рис.9 обозначена t1,0 — отрицательный и t0,1 — положительный. Величинами tзд.р.0,1 и tзд.р.1,0 обозначается время задержки распространения сигнала от входа до выхода при переходе из 0 в 1 и наоборот (рис.9). Минимальная длительность импульса на входе элемента tи.мин пропорциональна среднему значению tзд.р.ср. равному полусумме tзд.р.0,1 и tзд.р.1,0. Максимальная частота входных импульсов Fмакс обратно пропорциональна tзд.р.ср. Из сказанного следует, что быстродействие элемента тем выше, чем меньше tзд.р.ср. Определения вышеуказанных величин с их отечественными и международными обозначениями приведены в разделе обозначения некоторых параметров микросхем. Быстродействие схемы зависит также от алгебраической формы представления ЛФ. Пусть y = a*b + c*a + d = a*(b+c)+d. Первой форме (ДНФ) соответствует схема (A), а второй — схема (B) см. рис.10. 1.14 ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛОГИЧЕСКИХ СХЕМАХ Отличие времени задержки tзд.р. от нуля при прохождении сигнала через логическую схему может приводить к возникновению помех в выходном сигнале. Эти помехи имеют вид коротких импульсов, и в некоторых случаях приводят к серьезным сбоям в работе схем. Рассмотрим устройство на рис.11. Если элементы схемы не вносят задержки сигнала, а x0 и x1 находятся в противофазе, т.е. x0 = x1) = 1. Если же каждый из пяти ЛЭ имеет задержку tзд.р., тогда x0′ запаздывает относительно x0 на 4tзд.р. и на выходе схемы возникает незапланированный «отрицательный» импульс (интервал 1..2), сдвинутый на tзд.р. элемента И-НЕ (интервал 0..1). Процесс прохождения входных сигналов до общего выхода называется состязаниями или «гонками». 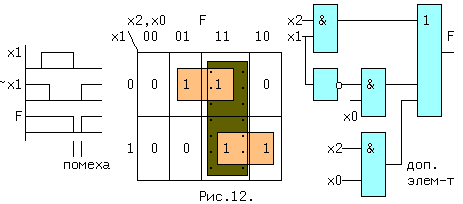Вредный эффект «гонок» может быть устранен несколькими способами, один из которых заключается в добавлении к ЛФ дополнительного слагаемого. Пусть некоторая ЛФ равна F = x1*x2 + x1*x0, тогда при x2=x0=1 может появиться помеха, вызванная тем, что сигнал x1 задержан относительно x1 на величину задержки инвертора (см. рис.12). Добавление лишнего импликанта (в таблице обведен точками) устраняет проблему, т.к.при критической ситуации, когда x2=x0=1, дополнительная составляющая x0*x2=1 и функция F = x1*x2 + x1*x0 + x0*x2 равна всегда 1 при x2=x0=1. В устройствах индикации такие короткие помехи можно игнорировать, так как они будут незаметны для глаз. Источник Читайте также:  Перечислите способы уборки зерновых культур Оцените статью Вам также может понравиться Ясень семена способ распространения Ясень обыкновенный Fraxinus excelsior – так в ботанической Ярлыки способы создания ярлыков ос windows Создаем ярлыки на рабочем столе Windows Создаем ярлыки Японское удобрение фуджима способ применения Удобрения Фуджима Знаете потрясающее удобрение, палочка Японский чай способ заварки Технология заваривания японского чая Известно, что Правообладателям Политика конфиденциальности Контакты