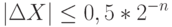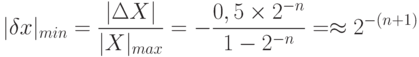Представление чисел в ЭВМ
Целые числа
Для числа +1101 :
| Прямой код | Обратный код | Дополнительный код |
| 0,0001101 | 0,0001101 | 0,0001101 |
Для числа -1101 :
| Прямой код | Обратный код | Дополнительный код |
| 1,0001101 | 1,1110010 | 1,1110011 |
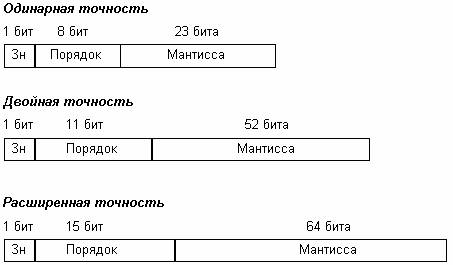
Вещественные числа (числа с плавающей точкой)
Пример .
Запишите код действительного числа, интерпретируя его как величину типа Double.
а) 446,15625;
Переводим десятичное число в двоичное представление.
| Целая часть от деления | Остаток от деления |
| 446 div 2 = 223 | 446 mod 2 = 0 |
| 223 div 2 = 111 | 223 mod 2 = 1 |
| 111 div 2 = 55 | 111 mod 2 = 1 |
| 55 div 2 = 27 | 55 mod 2 = 1 |
| 27 div 2 = 13 | 27 mod 2 = 1 |
| 13 div 2 = 6 | 13 mod 2 = 1 |
| 6 div 2 = 3 | 6 mod 2 = 0 |
| 3 div 2 = 1 | 3 mod 2 = 1 |
| 1 div 2 = 0 | 1 mod 2 = 1 |
Остаток от деления записываем в обратном порядке. Получаем число в 2-ой системе счисления: 110111110
446 = 1101111102
Для перевода дробной части числа последовательно умножаем дробную часть на основание 2. В результате каждый раз записываем целую часть произведения.
0.15625*2 = 0.313 (целая часть 0)
0.313*2 = 0.626 (целая часть 0)
0.626*2 = 1.252 (целая часть 1)
0.252*2 = 0.504 (целая часть 0)
0.504*2 = 1.008 (целая часть 1)
Получаем число в 2-ой системе счисления: 00101
0.15625 = 001012
446.15625 = 110111110,001012 = 1,1011111000101*2 8
Знак S = 0
Порядок P = 8 + 1023 = 103110 = 100000001112
Мантисса: 1011111000101
Для числа с двойной точностью мантисса занимает 52 разряда. Добавляем нули.
Мантисса: 1011 1110 0010 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000
Запишем число:
0 10000000111 1011 1110 0010 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000
В шестнадцатеричной системе счисления: 407BE2800000000016
б) -455,375.
Переводим десятичное число в двоичное представление.
| Целая часть от деления | Остаток от деления |
| 455 div 2 = 227 | 455 mod 2 = 1 |
| 227 div 2 = 113 | 227 mod 2 = 1 |
| 113 div 2 = 56 | 113 mod 2 = 1 |
| 56 div 2 = 28 | 56 mod 2 = 0 |
| 28 div 2 = 14 | 28 mod 2 = 0 |
| 14 div 2 = 7 | 14 mod 2 = 0 |
| 7 div 2 = 3 | 7 mod 2 = 1 |
| 3 div 2 = 1 | 3 mod 2 = 1 |
| 1 div 2 = 0 | 1 mod 2 = 1 |
Остаток от деления записываем в обратном порядке. Получаем число в 2-ой системе счисления: 111000111
455 = 1110001112
Для перевода дробной части числа последовательно умножаем дробную часть на основание 2. В результате каждый раз записываем целую часть произведения.
0.375*2 = 0.75 (целая часть 0)
0.75*2 = 1.5 (целая часть 1)
0.5*2 = 1 (целая часть 1)
0*2 = 0 (целая часть 0)
Получаем число в 2-ой системе счисления: 0110
0.375 = 01102
455,375 = 111000111,01102 = 1,110001110110*2 8 2
Знак S = 1
Порядок P = 8 + 1023 = 103110 = 100000001112
Мантисса: 1100 0111 0110 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000
Запишем число:
1 10000000111 1100 0111 0110 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000
В шестнадцатеричной системе счисления: -455,375 = C07C76000000000016
Дан код величины типа Double. Преобразуйте его число.
а) 408B894000000000;
Представим в двоичном коде:
010000001000 1011 1000 1001 0100 0000 0000 0000 0000 0000 0000 0000 0000 0000
где
S = 0 (положительное число)
P = 100000010002 = 1032 – 1023 = 9
M = 10111000100101
N = 1,10111000100101
С учетом P = 9, N = 1101110001,00101
1101110001 = 2 9 *1 + 2 8 *1 + 2 7 *0 + 2 6 *1 + 2 5 *1 + 2 4 *1 + 2 3 *0 + 2 2 *0+ 2 1 *0 + 2 0 *1 = 512 + 256 + 0 + 64 + 32 + 16 + 0 + 0 + 0 + 1 = 881
Для перевода дробной части необходимо разделить разряд числа на соответствующую ему степень разряда
00101 = 2 -1 *0 + 2 -2 *0 + 2 -3 *1 + 2 -4 *0 + 2 -5 *1 = 0.15625
б) C089930000000000.
Представим в двоичном коде:
1 10000001000 100110010011000000000000000000000000 0000 0000 0000 0000
где
S = 1 (отрицательное число)
P = 100000010002 = 1032 – 1023 = 9
M = 100110010011
N =1,100110010011
С учетом P = 9, N = 1100110010,011
1100110010 = 2 9 *1 + 2 8 *1 + 2 7 *0 + 2 6 *0 + 2 5 *1 + 2 4 *1 + 2 3 *0 + 2 2 *0 + 2 1 *1 + 2 0 *0 = 512 + 256 + 0 + 0 + 32 + 16 + 0 + 0 + 2 + 0 = 818
Для перевода дробной части необходимо разделить разряд числа на соответствующую ему степень разряда
011 = 2 -1 *0 + 2 -2 *1 + 2 -3 *1 = 0.375
Источник
Способы представления чисел в ЭВМ
Как мы уже знаем, применяются два основных способа представления чисел — с фиксированной и плавающей запятой . Большинство универсальных ЭВМ работает с числами, представленными с плавающей запятой , а большинство специализированных — с фиксированной запятой .
Однако целый ряд машин работает с числами в этих двух форматах.
В общем виде способ представления чисел сильно влияет на характер программирования. Так, программирование для ЭВМ, работающих в системе с фиксированной запятой , значительно усложняется, поскольку помимо алгоритмических трудностей этот процесс требует ещё отслеживания положения запятой.
Фиксированная запятая
Оговоримся, что разрядная сетка машины имеет постоянное число разрядов — n .
При представлении чисел с фиксированной запятой считают, что запятая всегда находится перед старшим разрядом, а все числа, которые участвуют в вычислениях, считаются по абсолютной величине меньше единицы:
Введём две характеристики чисел: диапазон изменения и точность представления.
Диапазон изменения характеризуется теми пределами, в которых могут находиться числа, с которыми оперирует машина.
Отличное от нуля самое малое число:
Таким образом, диапазон чисел, с которыми работает ЭВМ, есть:
Иными словами, числа, которые выходят за диапазон изменения, в ЭВМ не могут быть представлены точно. Если
то такое число воспринимается как нуль.
то такое число воспринимается как бесконечно большое. Этим двум случаям соответствуют понятия машинного нуля и машинной бесконечности .
При оптимальном округлении абсолютная ошибка:
Минимальная относительная ошибка:
так как 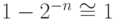
Максимальная относительная ошибка:
Ошибка представления числа зависит от величины самого числа и способа округления:
Заметим, что для малых чисел ошибка может достигать большой величины.
Источник
Способы представления чисел в ЭВМ
Как мы уже знаем, применяются два основных способа представления чисел — с фиксированной и плавающей запятой . Большинство универсальных ЭВМ работает с числами, представленными с плавающей запятой , а большинство специализированных — с фиксированной запятой .
Однако целый ряд машин работает с числами в этих двух форматах.
В общем виде способ представления чисел сильно влияет на характер программирования. Так, программирование для ЭВМ, работающих в системе с фиксированной запятой , значительно усложняется, поскольку помимо алгоритмических трудностей этот процесс требует ещё отслеживания положения запятой.
Фиксированная запятая
Оговоримся, что разрядная сетка машины имеет постоянное число разрядов — n .
При представлении чисел с фиксированной запятой считают, что запятая всегда находится перед старшим разрядом, а все числа, которые участвуют в вычислениях, считаются по абсолютной величине меньше единицы:
Введём две характеристики чисел: диапазон изменения и точность представления.
Диапазон изменения характеризуется теми пределами, в которых могут находиться числа, с которыми оперирует машина.
Отличное от нуля самое малое число:
Таким образом, диапазон чисел, с которыми работает ЭВМ, есть:
Иными словами, числа, которые выходят за диапазон изменения, в ЭВМ не могут быть представлены точно. Если
то такое число воспринимается как нуль.
то такое число воспринимается как бесконечно большое. Этим двум случаям соответствуют понятия машинного нуля и машинной бесконечности .
При оптимальном округлении абсолютная ошибка:
Минимальная относительная ошибка:
так как 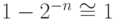
Максимальная относительная ошибка:
Ошибка представления числа зависит от величины самого числа и способа округления:
Заметим, что для малых чисел ошибка может достигать большой величины.
Источник