Способы повышения кпд простых механизмов

Простые механизмы. КПД простых механизмов

1. Простые механизмы — приспособления, которые сконструировал и использовал человек, чтобы облегчить работу по перемещению тяжёлых предметов. К ним относят: рычаг, блок, наклонную плоскость. Разновидностями этих механизмов являются: клин, ворот и винт.

Все простые механизмы позволяют преобразовать силу, действующую на тело: либо уменьшить её, либо изменить её направление.

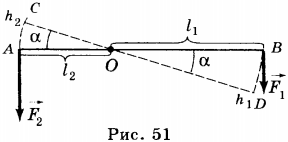
2. Рычаг — это стержень, вращающийся вокруг неподвижной опоры или оси (рис. 51). На рисунке показан рычаг, который может вращаться вокруг точки О, расположенный между концами рычага. К одному концу рычага подвешен груз, действующий на рычаг с силой ​ \( F_1 \) ​, равной весу груза. Действуя на длинный конец рычага с силой ​ \( F_2 \) ​, человек поднимает груз. При этом сила \( F_1 \) ​ стремится повернуть рычаг по часовой стрелке, а груз \( F_2 \) — против часовой стрелки.

Плечом силы называют кратчайшее расстояние (перпендикуляр) от точки опоры до линии действия силы. Так, плечом силы ​ \( F_1 \) ​ является расстояние ОА ​ \( (l_1) \) ​, плечом силы \( F_2 \) — расстояние ОВ \( (l_2) \) .

Из эксперимента следует, что рычаг находится в равновесии, если произведение силы, вращающей рычаг по часовой стрелке, и её плеча равно произведению силы, вращающей рычаг против часовой стрелки, и её плеча, т.е. ​ \( F_1l_1=F_2l_2 \) ​. Произведение силы, действующей на рычаг, и её плеча называют моментом силы: ​ \( Fl=M \) ​. Соответственно, если рычаг находится в равновесии, то ​ \( M_1=M_2 \) ​.

Условие равновесия рычага можно записать по-другому:​ \( \frac=\frac \) ​. Это равенство означает, что рычаг находится в равновесии, если силы, действующие на него, обратно пропорциональны их плечам. Оно называется условием равновесия рычага.

Рычаг другого типа вращается вокруг точки, находящейся на конце рычага. Примером такого рычага может служить тачка. Когда используется такой рычаг, то вес груза направлен вниз, а человек действует на свободный конец рычага с силой, направленной вверх. Для такого рычага также справедливо условие равновесия, приведенное выше.

3. При подъеме груза работа силы, действующей на груз, равна ​ \( A_1=F_1h_1 \) ​, работа силы, приложенной к другому концу рычага, равна \( A_2=F_2h_2 \) . Рассмотрение треугольников AOC и BOD позволяет сделать вывод о том, что они подобны и ​ \( \frac=\frac \) ​ или ​ \( \frac=\frac \) .​ Поскольку ​ \( F_1l_1=F_2l_2 \) ​, то ​ \( F_1h_1=F_2h_2 \) ​, т.е. ​ \( A_1=2 \) ​. Таким образом, рычаг, позволяя выиграть в силе, не даёт выигрыша в работе.

4. Ещё одним простым механизмом является блок. Блок — это колесо с желобом, по которому пропускается трос и которое может вращаться относительно оси О (см. рис. ниже).

Если ось блока закреплена, то блок не перемещается, и он называется неподвижным.

Неподвижный блок можно рассматривать как рычаг, вращающийся вокруг точки, лежащей посередине рычага. Плечи такого рычага равны друг другу: OA = OB. В соответствии с условием равновесия рычага приложенные к блоку силы тоже равны: ​ \( P=F \) ​. Следовательно, неподвижный блок не даёт выигрыша в силе, но он позволяет поднимать груз, прикладывая силу, направленную не вверх, а вниз, что облегчает перемещение груза.

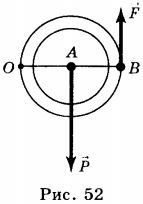
Чтобы получить выигрыш в силе используют подвижный блок (рис. 53). К нему непосредственно прикрепляется груз, один конец троса закрепляется, а к другому прикладывают силу и, таким образом, перебирая трос, поднимают блок с грузом.

В этом случае точкой вращения блока является точка А (см. рис. 52).

Плечи действующих сил равны соответственно: AO и AB, при этом AB = 2AO. В соответствии с условием равновесия рычага: ​ \( P=2F \) ​. Таким образом, подвижный блок даёт выигрыш в силе в 2 раза: ​ \( F=P/2 \) ​.

Измерив расстояние ​ \( h_1 \) ​, которое проходит груз, и расстояние ​ \( h_2 \) ​, на которое перемещается конец троса, можно обнаружить, что расстояние ​ \( h_2=2h_1 \) ​. Таким образом, подвижный блок даёт выигрыш в силе в 2 раза и в 2 раза проигрыш в пути. Соответственно, работа ​ \( Ph_1=Fh_2 \) ​, т.е. ​ \( A_1=2 \) ​. Подвижный блок, так же как и рычаг, не даёт выигрыша в работе.

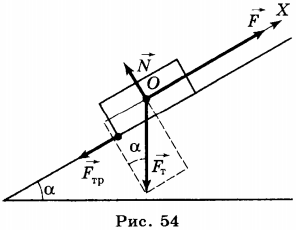
5. Наклонная плоскость используется в том случае, если нужно поднять объемный тяжёлый груз на какую-либо высоту (рис. 54).

Например, нужно погрузить ящик с металлическими деталями в кузов грузовика. В этом случае кладут массивную доску так, что она образует наклонную плоскость, один конец которой находится на земле, а другой на грузовике, и по этой плоскости втаскивают ящик. Чтобы поднять ящик вертикально вверх нужно приложить к нему силу, равную его весу ​ \( P \) ​. Перемещая равномерно ящик по наклонной плоскости, в отсутствие трения прикладывают силу, равную ​ \( F=P\sin\alpha \) ​, т.е. меньшую веса ящика, но при этом, выигрывая в силе, проигрывают в расстоянии. Работа по подъёму ящика по вертикали равна работе, совершаемой при его перемещении вдоль наклонной плоскости. Это справедливо, если сила сопротивления движению пренебрежимо мала. При наличии трения перемещение ящика вдоль наклонной плоскости требует совершения большей работы, чем при его движении вертикально вверх. В этом случае говорят о коэффициенте полезного действия (КПД) наклонной плоскости. Он равен отношению полезной работы ко всей совершённой работе: ​ \( \mathbf<КПД>=A_п/A_с\cdot 100 \% \) ​, где ​ \( A_п \) ​ — полезная работа, ​ \( A_п=mgh \) ​; ​ \( A_с \) ​ — совершённая работа при перемещении ящика вдоль наклонной плоскости, ​ \( A_c=Fl \) ​, где ​ \( F \) ​ — приложенная сила, ​ \( l \) ​ — длина наклонной плоскости.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Исследуя условия равновесия рычага, ученик выполнил соответствующую лабораторную работу. В таблице представлены значения сил и их плеч для рычага, находящегося в равновесии. Определите, чему равно плечо ​ \( l_1 \) ​?

1) 12,8 м
2) 2,5 м
3) 0,8 м
4) 0,25 м

2. Ученик выполнял лабораторную работу по исследованию условий равновесия рычага. Результаты для сил и их плеч, которые он получил, представлены в таблице.

Чему равна сила ​ \( F_1 \) ​, если рычаг находится в равновесии?

1) 100 Н
2) 50 Н
3) 25 Н
4) 9 Н

3. Рычаг находится в равновесии под действием двух сил. Сила ​ \( F_1 \) ​ = 6 Н. Чему равна сила \( F_2 \) , если длина рычага 50 см, а плечо силы \( F_1 \) равно 30 см?

1) 0,1 Н
2) 3,6 Н
3) 9 Н
4) 12 Н

4. Выигрыш в силе, приложенной к грузу, нельзя получить с помощью

1) подвижного блока
2) неподвижного блока
3) рычага
4) наклонной плоскости

5. С помощью неподвижного блока в отсутствие трения силе

1) выигрывают в 2 раза
2) не выигрывают, но и не проигрывают
3) проигрывают в 2 раза
4) возможен и выигрыш, и проигрыш

6. С помощью подвижного блока в отсутствие трения

1) выигрывают в работе в 2 раза
2) проигрывают в силе в 2 раза
3) не выигрывают в силе
4) выигрывают в силе в 2 раза

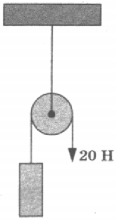
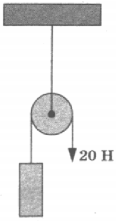
7. На рисунке изображён неподвижный блок, с помощью которого, прикладывая к свободному концу нити силу 20 Н, равномерно поднимают груз. Если трением пренебречь, то масса поднимаемого груза равна

1) 4 кг
2) 2 кг
3) 0,5 кг
4) 1 кг

8. Наклонная плоскость даёт выигрыш в силе в 2 раза. В работе при отсутствии силы трения эта плоскость

1) даёт выигрыш в 2 раза
2) даёт выигрыш в 4 раза
3) не даёт ни выигрыша, ни проигрыша
4) даёт проигрыш в 2 раза

9. Вдоль наклонной плоскости длиной 5 м поднимают груз массой 40 кг, прикладывая силу 160 Н. Чему равна высота наклонной плоскости, если трение при движении груза пренебрежимо мало?

1) 1,25 м
2) 2 м
3) 12,5 м
4) 20 м

10. Груз массой 10 кг поднимают по наклонной плоскости длиной 2 м и высотой 0,5 м, прикладывая силу 40 Н. Чему равен КПД наклонной плоскости?

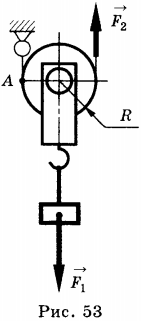
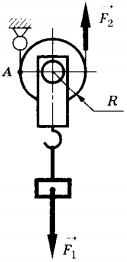
11. Груз поднимают с помощью подвижного блока радиусом ​ \( R \) ​ (см. рисунок). Установите соответствие между физическими величинами (левый столбец) и формулами, по которым они определяются (правый столбец).

Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) плечо силы ​ \( \vec_1 \) ​ относительно точки A
Б) плечо силы \( \vec_2 \) относительно точки A
B) момент силы \( \vec_1 \) относительно точки A

ФОРМУЛЫ
1) ​ \( F_1R \) ​
2) \( 2F_1R \)
3) \( \frac \)
4) ​ \( R \) ​
5) ​ \( 2R \) ​

12. Из перечня приведённых ниже высказываний выберите два правильных и запишите их номера в таблицу.

1) Любой простой механизм даёт выигрыш в силе.
2) Ни один простой механизм не даёт выигрыша в работе.
3) Наклонная плоскость выигрыша в силе не даёт.
4) Коэффициент полезного действия показывает, какая часть совершенной работы является полезной.
5) Неподвижный блок даёт выигрыш в силе в 2 раза.

Часть 2

13. Чему равна сила, с которой действуют на брусок массой 0,2 кг, перемещая его по наклонной плоскости длиной 1,6 м и высотой 0,4 м, если КПД наклонной плоскости 80%.

Источник

Коэффициент полезного действия (КПД)

О чем эта статья:

КПД: понятие коэффициента полезного действия

Представьте, что вы пришли на работу в офис, выпили кофе, поболтали с коллегами, посмотрели в окно, пообедали, еще посмотрели в окно — вот и день прошел. Если вы не сделали ни одного дела по работе, то можно считать, что ваш коэффициент полезного действия равен нулю.

В обратной ситуации, когда вы сделали все запланированное — КПД равен 100%.

По сути, КПД — это процент полезной работы от работы затраченной.

Вычисляется по формуле:

Формула КПД

η = (Aполезная/Aзатраченная) * 100%

η — коэффициент полезного действия [%]

Aполезная — полезная работа [Дж]

Aзатраченная — затраченная работа [Дж]

Есть такое философское эссе Альбера Камю «Миф о Сизифе». Оно основано на легенде о неком Сизифе, который был наказан за обман. Его приговорили после смерти вечно таскать огромный булыжник вверх на гору, откуда этот булыжник скатывался, после чего Сизиф тащил его обратно в гору. То есть он делал совершенно бесполезное дело с нулевым КПД. Есть даже выражение «Сизифов труд», которое описывает какое-либо бесполезное действие.

Давайте пофантазируем и представим, что Сизифа помиловали и камень с горы не скатился. Тогда, во-первых, Камю бы не написал об этом эссе, потому что никакого бесполезного труда не было. А во-вторых, КПД в таком случае был бы не нулевым.

Полезная работа в этом случае равна приобретенной булыжником потенциальной энергии. Потенциальная энергия прямо пропорционально зависит от высоты: чем выше расположено тело, тем больше его потенциальная энергия. То есть, чем выше Сизиф прикатил камень, тем больше потенциальная энергия, а значит и полезная работа.

Потенциальная энергия

Еп = mg

Еп — потенциальная энергия [Дж]

m — масса тела [кг]

g — ускорение свободного падения [м/с^2]

На планете Земля g ≃ 9,8 м/с^2

Затраченная работа здесь — это механическая работа Сизифа. Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.

Механическая работа

А = FS

A — механическая работа [Дж]

F — приложенная сила [Н]

И как же достоверно определить, какая работа полезная, а какая затраченная?

Все очень просто! Задаем два вопроса:

1. За счет чего происходит процесс?
2. Ради какого результата?

В примере выше процесс происходит ради того, чтобы тело поднялось на какую-то высоту, а значит — приобрело потенциальную энергию (для физики это синонимы). Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.

КПД в механике

Главный секрет заключается в том, что эта формула подойдет для всех видов КПД.

КПД

η = (Aполезная/Aзатраченная) * 100%

η — коэффициент полезного действия [%]

Aполезная — полезная работа [Дж]

Aзатраченная — затраченная работа [Дж]

Дальше мы просто заменяем полезную и затраченную работы на те величины, которые ими являются.

Давайте разберемся на примере задачи.

Задача

Чтобы вкатить санки массой 4 кг в горку длиной 12 метров, мальчик приложил силу в 15 Н. Высота горки равна 2 м. Найти КПД этого процесса. Ускорение свободного падения принять равным g ≃9,8 м/с^2

Запишем формулу КПД.

η = (Aполезная/Aзатраченная) * 100%

Теперь задаем два главных вопроса:

Ради чего все это затеяли?

Чтобы санки в горку поднять — то есть ради приобретения телом потенциальной энергии. Значит в данном процессе полезная работа равна потенциальной энергии санок.

Потенциальная энергия

Еп = mgh

Еп — потенциальная энергия [Дж]

m — масса тела [кг]

g — ускорение свободного падения [м/с^2]

На планете Земля g ≃9,8 м/с^2

За счет чего процесс происходит?

За счет мальчика, он же тянет санки. Значит затраченная работа равна механической работе

Механическая работа

А = FS

A — механическая работа [Дж]

F — приложенная сила [Н]

Заменим формуле КПД полезную работу на потенциальную энергию, а затраченную — на механическую работу:

η = Eп/A * 100% = mgh/FS * 100%

η = 4*9,8*2/15*12 * 100% = 78,4/180 * 100% ≃ 43,6 %

Ответ: КПД процесса приблизительно равен 43,6 %

КПД в термодинамике

В термодинамике КПД — очень важная величина. Она полностью определяет эффективность такой штуки, как тепловая машина.

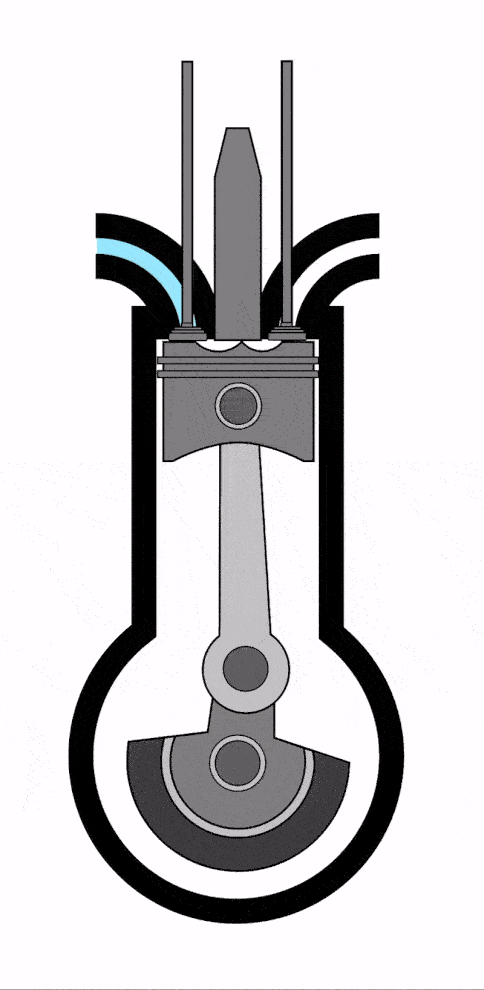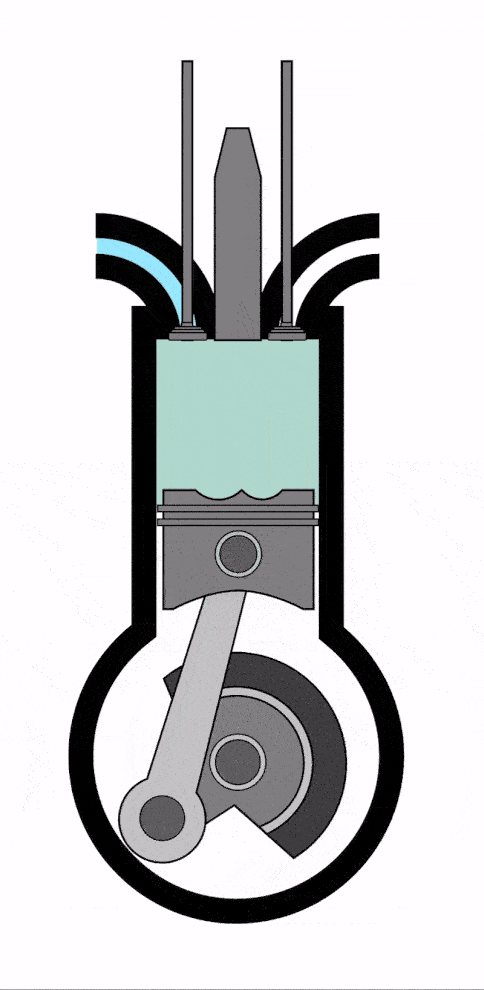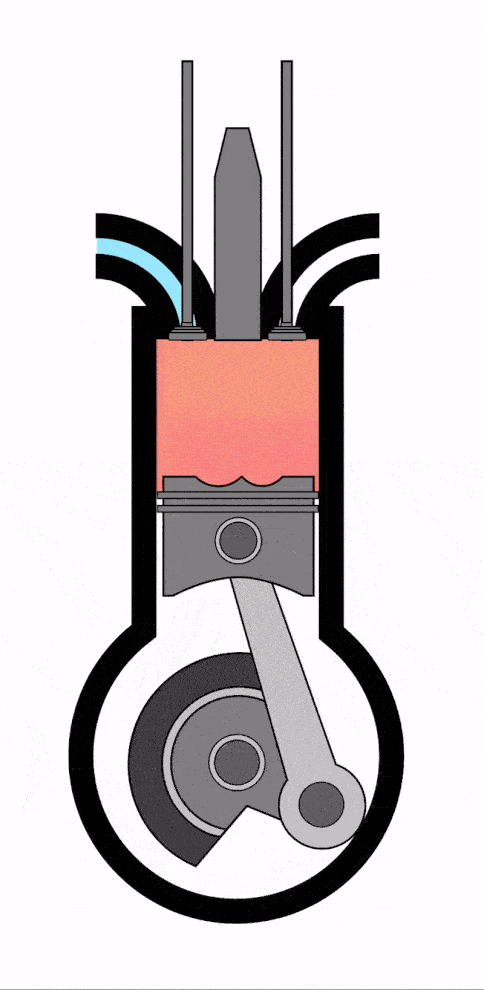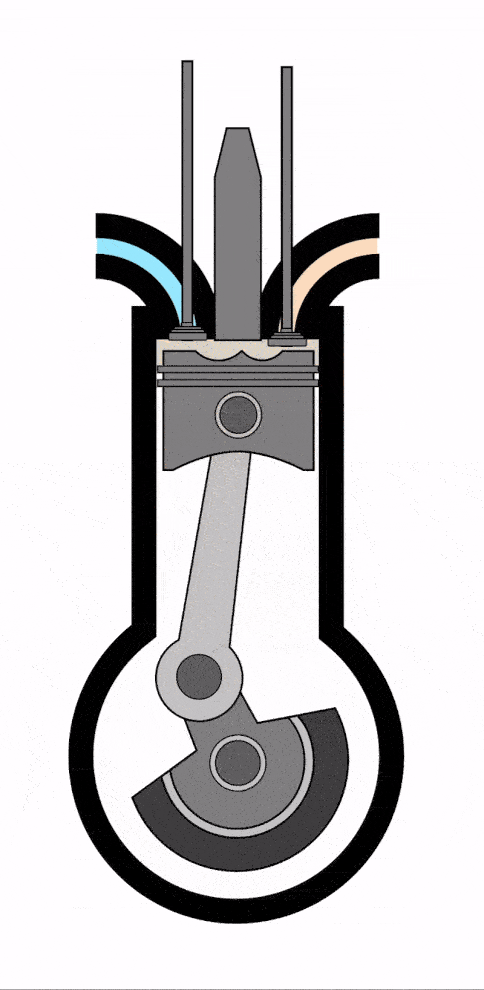
• Тепловой двигатель (машина) – это устройство, которое совершает механическую работу циклически за счет энергии, поступающей к нему в ходе теплопередачи.

Схема теплового двигателя выглядит так:

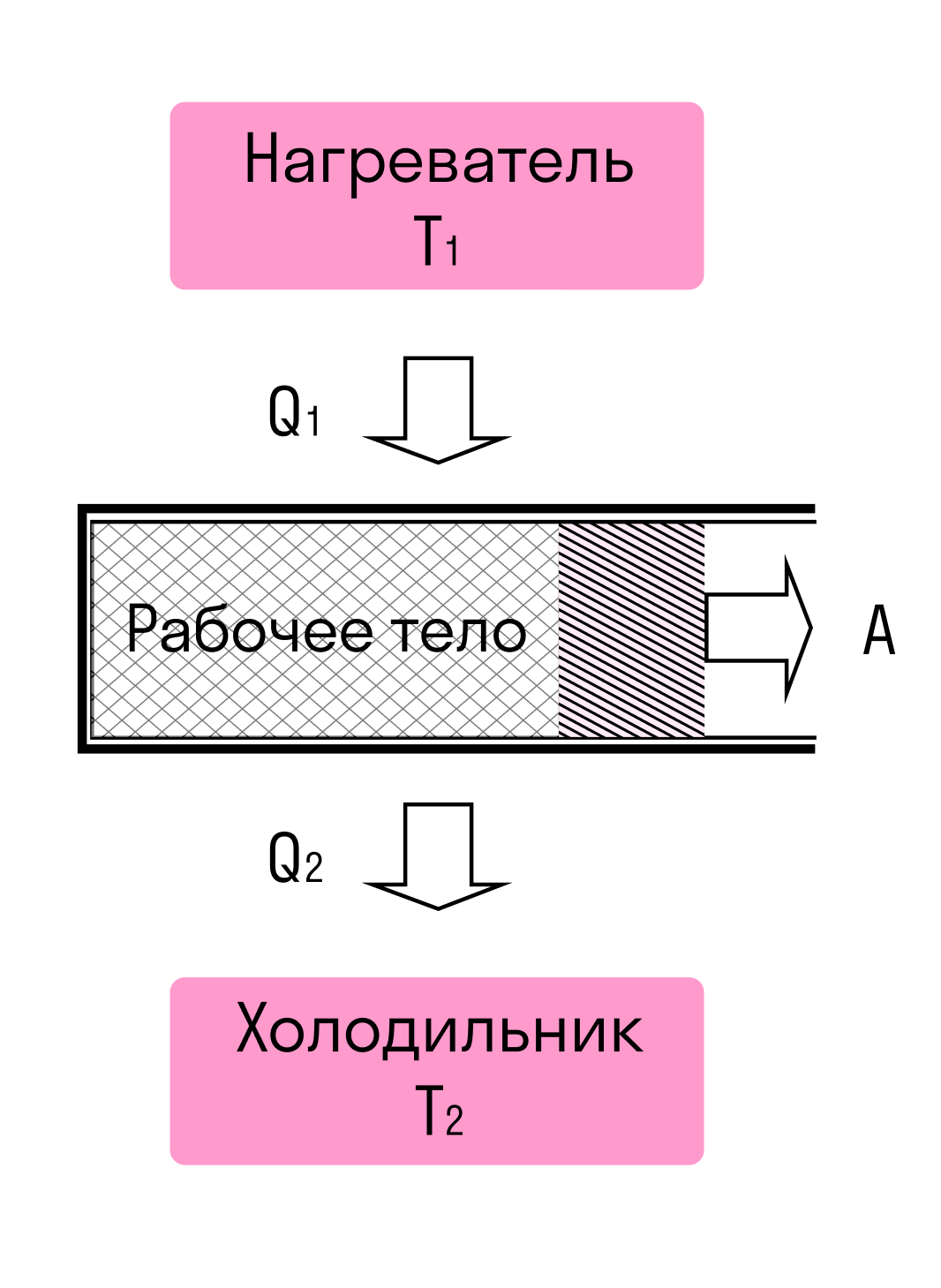
У теплового двигателя обязательно есть нагреватель, который (не может быть!) нагревает рабочее тело, передавая ему количество теплоты Q1 или Qнагревателя (оба варианта верны, это зависит лишь от учебника, в котором вы нашли формулу).

• Рабочее тело — это тело, на котором завязан процесс (чаще всего это газ). Оно расширяется при подводе к нему теплоты и сжимается при охлаждении. Часть переданного Q1 уходит на механическую работу A. Из-за этого производится движение.

Оставшееся количество теплоты Q2 или Qхолодильника отводится к холодильнику, после чего возвращается к нагревателю и процесс повторяется.

КПД такой тепловой машины будет равен:

КПД тепловой машины

η = (Aполезная/Qнагревателя) * 100%

η — коэффициент полезного действия [%]

Aполезная — полезная работа (механическая) [Дж]

Qнагревателя — количество теплоты, полученное от нагревателя[Дж]

Если мы выразим полезную (механическую) работу через Qнагревателя и Qхолодильника, мы получим:

A = Qнагревателя — Qхолодильника.

Подставим в числитель и получим такой вариант формулы.

КПД тепловой машины

η = Qнагревателя — Qхолодильника/Qнагревателя * 100%

η — коэффициент полезного действия [%]

Qнагревателя — количество теплоты, полученное от нагревателя[Дж]

Qхолодильника — количество теплоты, отданное холодильнику [Дж]

А возможно ли создать тепловую машину, которая будет работать только за счет охлаждения одного тела?

Точно нет! Если у нас не будет нагревателя, то просто нечего будет передавать на механическую работу. Любой такой процесс — когда энергия не приходит из ниоткуда — означал бы возможность существования вечного двигателя.

Поскольку свидетельств такого процесса в мире не существует, то мы можем сделать вывод: вечный двигатель невозможен. Это второе начало термодинамики.

Запишем его, чтобы не забыть:

Невозможно создать периодическую тепловую машину за счет охлаждения одного тела без изменений в других телах.

Задача

Найти КПД тепловой машины, если рабочее тело получило от нагревателя 20кДж, а отдало холодильнику 10 кДж.

Решение:

Возьмем формулу для расчета КПД:

η = Qнагревателя — Qхолодильника/Qнагревателя * 100%

η = 20 — 10/20 *100% = 50%

Ответ: КПД тепловой машины равен 50%

Идеальная тепловая машина: цикл Карно

Давайте еще чуть-чуть пофантазируем: какая она — идеальная тепловая машина. Кажется, что это та, у которой КПД равен 100%.

На самом деле понятие «идеальная тепловая машина» уже существует. Это тепловая машина, у которой в качестве рабочего тела взят идеальный газ. Такая тепловая машина работает по циклу Карно. Зависимость давления от объема в этом цикле выглядит следующим образом

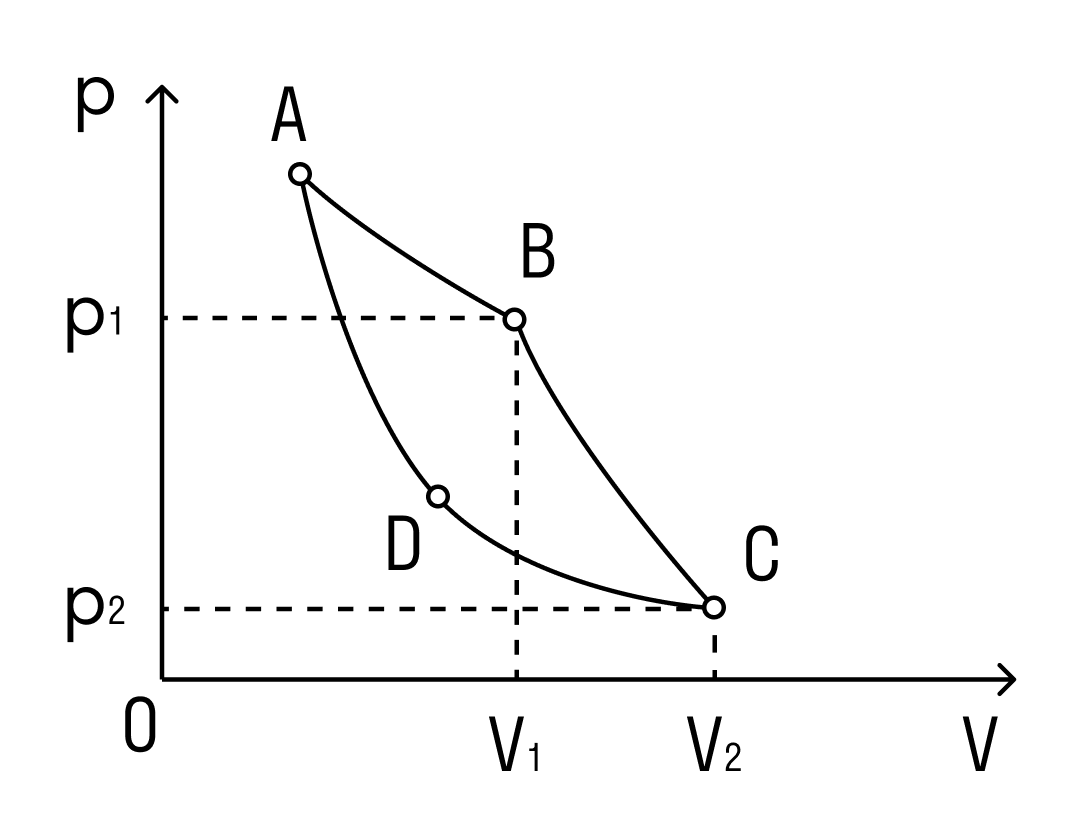
А КПД для цикла Карно можно найти через температуры нагревателя и холодильника.

КПД цикла Карно

η = Tнагревателя — Tхолодильника /Tнагревателя *100%

η — коэффициент полезного действия [%]

Tнагревателя — температура нагревателя[Дж]

Tхолодильника — температура холодильника [Дж]

КПД в электродинамике

Мы каждый день пользуемся различными электронными устройствами: от чайника до смартфона, от компьютера до робота-пылесоса — и у каждого устройства можно определить, насколько оно эффективно выполняет задачу, для которой оно предназначено, просто посчитав КПД.

КПД

η = Aполезная/Aзатраченная *100%

η — коэффициент полезного действия [%]

Aполезная — полезная работа [Дж]

Aзатраченная — затраченная работа [Дж]

Для электрических цепей тоже есть нюансы. Давайте разбираться на примере задачи.

Задачка, чтобы разобраться

Найти КПД электрического чайника, если вода в нем приобрела 22176 Дж тепла за 2 минуты, напряжение в сети — 220 В, а сила тока в чайнике 1,4 А.

Решение:

Цель электрического чайника — вскипятить воду. То есть его полезная работа — это количество теплоты, которое пошло на нагревание воды. Оно нам известно, но формулу вспомнить все равно полезно 😉

Количество теплоты, затраченное на нагревание

Q — количество теплоты [Дж]

c — удельная теплоемкость вещества [Дж/кг*˚C]

tконечная — конечная температура [˚C]

tначальная — начальная температура [˚C]

Работает чайник, потому что в розетку подключен. Затраченная работа в данном случае — это работа электрического тока.

Работа электрического тока

A = (I^2)*Rt = (U^2)/R *t = UIt

A — работа электрического тока [Дж]

U — напряжение [В]

R — сопротивление [Ом]

То есть в данном случае формула КПД будет иметь вид:

η = Q/A *100% = Q/UIt *100%

Переводим минуты в секунды — 2 минуты = 120 секунд. Теперь намм известны все значения, поэтому подставим их:

η = 22176/220*1,4*120 *100% = 60%

Ответ: КПД чайника равен 60%.

Давайте выведем еще одну формулу для КПД, которая часто пригождается для электрических цепей, но применима ко всему. Для этого нужна формула работы через мощность:

Работа электрического тока

A — работа электрического тока [Дж]

Подставим эту формулу в числитель и в знаменатель, учитывая, что мощность разная — полезная и затраченная. Поскольку мы всегда говорим об одном процессе, то есть полезная и затраченная работа ограничены одним и тем же промежутком времени, можно сократить время и получить формулу КПД через мощность.

КПД

η = Pполезная/Pзатраченная *100%

η — коэффициент полезного действия [%]

Pполезная — полезная мощность [Дж]

Pзатраченная — затраченная мощность [Дж]

Источник