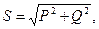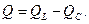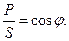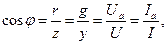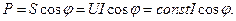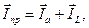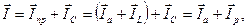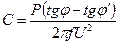Способы повышения коэффициента мощности цепи переменного тока

Коэффициент мощности и способы его повышения

Коэффициентом мощности называется отношение активной (средней за период) мощности Р к полной (кажущейся) мощности S.

(56)

коэффициент мощности =

Полная мощность, как это следует из треугольника мощности (рис. 29):

где Q – реактивная мощность. Кроме того, справедливы следующие соотношения: S = UI, P = UIcosφ, Q = UIsinφ, где U, I, φ – соответственно действующие значения напряжения и тока и угол сдвига по фазе между напряжением и током на входе потребителя переменного тока. В общем случае результирующая реактивная мощность определяется как разность индуктивной Q_L и емкостной Q_C мощностей

(57)

Нетрудно видеть (рис. 29), что коэффициент мощности может быть представлен как косинус угла сдвига φ между напряжением и током

(58)

Коэффициент мощности можно также получить как отношение активной составляющей к полной величине: сопротивления или проводимости, напряжения или тока эквивалентной последовательной и параллельной цепей, то есть

(59)

как это следует из соответствующих подобных треугольников.

Как известно [2], площадь поперечного сечения проводов линий электропередач и электрических сетей, обмоток электрических машин и трансформаторов выбирается из условий нагрева, то есть по величине тока I, который при заданном напряжении пропорционален полной мощности S = UI. Энергия, преобразуемая из электрической необратимо в другие виды (механическую, тепловую, химическую и др.), то есть используемая человеком для практических целей, пропорциональна активной энергии и соответствующей ей активной мощности Р, которая, как следует из выражения (58), может быть представлена в виде:

(60)

Поскольку U = const (стандартная величина напряжения, подаваемого на зажимы приемника), то одна и та же величина активной мощности Р может передаваться приемнику при большем токе и низком cosφ, или меньшем токе и более высоком значении коэффициента мощности cosφ.

Поэтому выгодно повышать cosφ на входе приемника, поскольку при этом снижается ток I в питающей линии, что позволяет увеличить ее пропускную способность, то есть передать дополнительную активную мощность, а также снизить потери напряжения на входе приемника и потери энергии на нагревание проводов линии электропередачи.

Большинство приемников электрической энергии переменного тока имеет индуктивный характер, то есть они потребляют индуктивную мощность Q_L (асинхронные двигатели, трансформаторы, электромагниты, выпрямители, магнитные пускатели и т.д.). Для уменьшения индуктивной мощности, передаваемой по линии, и повышения тем самым cosφ существует ряд мероприятий, в том числе искусственное повышение cosφ с помощью батареи конденсаторов, которое рассмотрим в этом разделе применительно к однофазному активно-индуктивному приемнику или одной фазе симметричного трехфазного приемника.

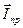
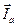
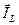
На рисунке 30а показана эквивалентная схема приемника, который представлен в виде двух параллельно включенных ветвей: активной r и катушки индуктивности L. Согласно первому закону Кирхгофа вектор действующее значение тока приемника равен геометрической сумме активного и индуктивного токов:

(61)

где величина тока .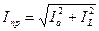

Векторная диаграмма напряжения U питающей линии и токов эквивалентной схемы показана на рисунке 30б. Если стороны заштрихованного векторного треугольника токов умножить на напряжение U, то получится подобный исходному треугольник мощностей приемника со сторонами P, Q и S (рис. 30б)

На рисунке 31а показана схема, на которой параллельно приемнику с помощью ключа K можно включить компенсирующий конденсатор с емкостью С.

Если ключ K разомкнут, то по питающей линии течет ток I = I_пр, чему соответствует векторная диаграмма на рисунке 30б.

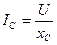
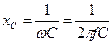
Чтобы уменьшить ток I линии, необходимо замкнуть ключ K (рис. 31а). При этом в цепи конденсатора потечет ток , опережая напряжение U на угол π/2, причем – емкостное сопротивление конденсатора при частоте питающей сети f = 50 Гц (ω = 2πf – угловая частота).

Согласно первому закону Кирхгофа при замкнутом ключе K (рис. 31а)

(62)

где I_p = I_L – I_C – реактивный ток, поступающий из сети. Соответствующая равенству (62) векторная диаграмма показана на рисунке 31б. Из диаграммы видно, что при включенном конденсаторе ток линии изменяется до величины I cosφ).

Оказывается, что экономически целесообразно повышать cosφ до величины cosφ¢ = 0,85¸0,9 при отстающем токе I, так как при достижении резонанса cosφ¢ = 1,0 или перекомпенсации, то есть опережающем токе (φ cosφ.

Можно показать, что величина емкости С при этом должна рассчитываться по формуле

(63)

Вывод этой зависимости приведен в [7].

Необходимо помнить, что при включении компенсирующего конденсатора (рис. 31а) сам приемник продолжает работать с тем же самым током I_пр и низким cosφ, а коэффициент мощности cosφ¢ повышается на входе всей установки, включающей сам приемник и компенсирующий конденсатор.

Источник

Коэфициент мощности, способы его повышения.

Коэффицие́нт мо́щности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.

Коэффициент мощности

показывает, насколько рационально используется электрическая энергия. Чем ближе , тем лучше, так как больше удельный вес Р в S, а именно активная мощность Р и совершает полезную работу.
Для повышения существует два способа:
1. Естественный способ. Для повышения можно использовать потребители, которые не используют реактивную мощность (машины постоянного тока); асинхронные двигатели, соответствующие требуемой мощности, или специальные электрические машины (синхронные компенсаторы).
2. Искусственный способ (рис. 1.21). Для повышения нужно уменьшить угол сдвига фаз между током и напряжением либо к нагрузке, носящей активно-индуктивный характер, параллельно подключить батарею емкостей.

Рис. 1.21. Схема (а) и векторная диаграмма (б) при искусственном
увеличении коэффициента мощности (––– – до подключения С;
— — — – после подключения С)

Для цепи, показанной на рис. 1.21, а, имеем
, .
Так как , то .

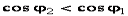
Трехфазная система ЭДС. Фазные и линейные напряжения.

Совокупность трех синусоид смещенных относительно друг друга во времени на 1/3 периода(120град).

Источником трехфазной цепи явл синхронный генератор который состоит из неподвижного статора и вращающегося ротора.

Ротор представляет собой электромагнит питаемый постоянным током

Статор состоит из сердечника и трех групп катушек(фаз).

Напряжения ua,ub,uc фазное напряжение генератора измеряют между началом и концом фазы.

Фазное либо между линейным и нейтральным проводом uab,ubc,uca uл линейное напряжение генератора измеряется между началом двух фаз, либо между двумя линейными проводами.

Классификация и способы включения приемников в трехфазную сеть.

Приемники трехфазной цепи может быть:

1)трехфазными(двигатели, трансформаторы, 3-фазное оборудование).

2)Однофазными(бытовые, осветительные приборы прочее).

Звезда

Принимается когда наминальное напряжение потребителя соотвествует фазному напряжению источника.

Применяется когда наминальное напряжение потребителя соотвествует линейному напряжению источника

Трехфазная сеть при соединении приемников по схеме «звезда».назначение нейтрального провода.

Соединение звезда может быть двух видов:

1)Четырехпроходная звезда или звезда с нейтральным проводом

Применяется при не симметричной нагрузке.

2)Звезда Четырехпроходная либо без нейтрального провода

Применяется при симметричной нагрузке.

UA,UB,UC-фазные напряжения источника

Ua,Ub,Uc-фазное напряжение потребителя

IA,IB,IC-линейны токи – токи проводящих проводов

Ia,Ib,Ic-фазные токи потребителя

Iа=

Ib=

Iа=

14.Трехфазная цепь при соединении приемников по схеме «треугольник ».Симметричный режим работы.

Мощность трехфазной цепи.

Активная и реактивная мощности трехфазной цепи, как для любой сложной цепи, равны суммам соответствующих мощностей отдельных фаз:

В симметричном режиме мощности отдельных фаз равны, а мощность всей цепи может быть получена путем умножения фазных мощностей на число фаз:

В полученных выражениях заменим фазные величины на линейные. Для схемы звезды верны соотношения Uф/Uл/√3, I_ф=I_л, тогда получим:

Для схемы треугольника верны соотношения: Uф=Uл ; Iф=Iл / √3 , тогда получим:

Следовательно, независимо от схемы соединения (звезда или треугольник) для симметричной трехфазной цепи формулы для мощностей имеют одинаковый вид:

В приведенных формулах для мощностей трехфазной цепи подразумеваются линейные значения величин U и I, но индексы при их обозначениях не ставятся.

Активная мощность в электрической цепи измеряется прибором, называемым ваттметром, показания которого определяется по формуле:

где U_w, I_w — векторы напряжения и тока, подведенные к обмоткам прибора.

Для измерения активной мощности всей трехфазной цепи в зависимости от схемы соединения фаз нагрузки и ее характера применяются различные схемы включения измерительных приборов. Для измерения активной мощности симметричной трехфазной цепи применяется схема с одним ваттметром, который включается в одну из фаз и измеряет активную мощность только этой фазы. Активная мощность всей цепи получается путем умножения показания ваттметра на число фаз: P=3W=3U_фI_фcos(φ). Схема с одним ваттметром может быть использована только для ориентированной оценки мощности и неприменима для точных и коммерческих измерений.

При отсутствии нулевого провода линейные (фазные) ток связаны между собой уравнением 1-го закона Кирхгофа: I_A+I_B+I_C=0. Сумма показаний двух ваттметров равна:

Таким образом, сумма показаний двух ваттметров равна активной трехфазной мощности, при этом показание каждого прибора в отдельности зависит не только величины нагрузки но и от ее характера.

На рис. 40.4 показана векторная диаграмма токов и напряжений для симметричной нагрузки. Из диаграммы следует, что показания отдельных ваттметров могут быть определены по формулам:

16.Переходные процессы в линейных электрических цепях, основные понятия ,законы.

Переходный процесс возникает в электрической цепи призматического режима ее работы под воздействием выключений при включении и выключении источников,потребителей либо при аварийных режимах на участках цепи(ХХ и КЗ).Переходный процесс с индуктивностью либо емкостью не может протекать мгновенно,т.к.энергия магнитного поля индуктивности или электрического поля емкости не может изменяться скачком.Любое изменение в электрической цепи вызывает изменение режима работы,наз коммутацией.

Законы коммутации:1) Ток индуктивного элемента не может изменяться скачком. Il(-0)=Il(0)=Il(+0);2)Напряжение на емкостном элементе не может изменяться скачком Uc(-0)= Uc (0)= Uc (+0)

17.Переходные процессы в электрической цепи с индуктивным элементов.(рассмотреть на примере задачи)

Электромагнит постоянного тока имеет сопротивление R=11 Ом и индуктивность L=0,44 Гн. Напряжение источника U=220 В. Рассчитать сопротивление R_p реостата, шунтирующего обмотку электромагнита, при котором напряжение на обмотке в момент отключения электромагнита не превысит утроенного значения напряжения источника.

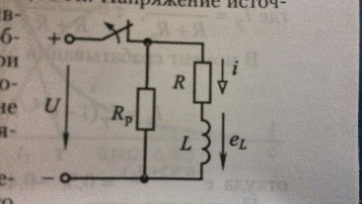
Решение. Установившееся значение тока электромагнита, включенного под напряжение, I=U/R=20 А. Электрическое состояние цепи при отключенном источнике напряжения характеризуется уравнением

Решение которого i=Ae -(R+R _p )/ L * t .

Поскольку ток в индуктивности не изменяется скачком, то в момент размыкания ключа(t=0) i(0)=20=Ae 0 , значит А=20, и ток в переходном режиме

Напряжение на обмотке электромагнита

Сопротивление R_p расчитываем так, что бы в момент отключения (t=0) u_ЭМ было больше либо равно 3U:

3U>=20 R_pe 0 ; R_p Pt P-корень 1+RCP=0

Источник