Способы повышения коэффициента мощности реферат

Коэфициент мощности, способы его повышения.

Коэффицие́нт мо́щности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.

Коэффициент мощности

показывает, насколько рационально используется электрическая энергия. Чем ближе , тем лучше, так как больше удельный вес Р в S, а именно активная мощность Р и совершает полезную работу.
Для повышения существует два способа:
1. Естественный способ. Для повышения можно использовать потребители, которые не используют реактивную мощность (машины постоянного тока); асинхронные двигатели, соответствующие требуемой мощности, или специальные электрические машины (синхронные компенсаторы).
2. Искусственный способ (рис. 1.21). Для повышения нужно уменьшить угол сдвига фаз между током и напряжением либо к нагрузке, носящей активно-индуктивный характер, параллельно подключить батарею емкостей.

Рис. 1.21. Схема (а) и векторная диаграмма (б) при искусственном
увеличении коэффициента мощности (––– – до подключения С;
— — — – после подключения С)

Для цепи, показанной на рис. 1.21, а, имеем
, .
Так как , то .

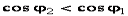
Трехфазная система ЭДС. Фазные и линейные напряжения.

Совокупность трех синусоид смещенных относительно друг друга во времени на 1/3 периода(120град).

Источником трехфазной цепи явл синхронный генератор который состоит из неподвижного статора и вращающегося ротора.

Ротор представляет собой электромагнит питаемый постоянным током

Статор состоит из сердечника и трех групп катушек(фаз).

Напряжения ua,ub,uc фазное напряжение генератора измеряют между началом и концом фазы.

Фазное либо между линейным и нейтральным проводом uab,ubc,uca uл линейное напряжение генератора измеряется между началом двух фаз, либо между двумя линейными проводами.

Классификация и способы включения приемников в трехфазную сеть.

Приемники трехфазной цепи может быть:

1)трехфазными(двигатели, трансформаторы, 3-фазное оборудование).

2)Однофазными(бытовые, осветительные приборы прочее).

Звезда

Принимается когда наминальное напряжение потребителя соотвествует фазному напряжению источника.

Применяется когда наминальное напряжение потребителя соотвествует линейному напряжению источника

Трехфазная сеть при соединении приемников по схеме «звезда».назначение нейтрального провода.

Соединение звезда может быть двух видов:

1)Четырехпроходная звезда или звезда с нейтральным проводом

Применяется при не симметричной нагрузке.

2)Звезда Четырехпроходная либо без нейтрального провода

Применяется при симметричной нагрузке.

UA,UB,UC-фазные напряжения источника

Ua,Ub,Uc-фазное напряжение потребителя

IA,IB,IC-линейны токи – токи проводящих проводов

Ia,Ib,Ic-фазные токи потребителя

Iа=

Ib=

Iа=

14.Трехфазная цепь при соединении приемников по схеме «треугольник ».Симметричный режим работы.

Мощность трехфазной цепи.

Активная и реактивная мощности трехфазной цепи, как для любой сложной цепи, равны суммам соответствующих мощностей отдельных фаз:

В симметричном режиме мощности отдельных фаз равны, а мощность всей цепи может быть получена путем умножения фазных мощностей на число фаз:

В полученных выражениях заменим фазные величины на линейные. Для схемы звезды верны соотношения Uф/Uл/√3, I_ф=I_л, тогда получим:

Для схемы треугольника верны соотношения: Uф=Uл ; Iф=Iл / √3 , тогда получим:

Следовательно, независимо от схемы соединения (звезда или треугольник) для симметричной трехфазной цепи формулы для мощностей имеют одинаковый вид:

В приведенных формулах для мощностей трехфазной цепи подразумеваются линейные значения величин U и I, но индексы при их обозначениях не ставятся.

Активная мощность в электрической цепи измеряется прибором, называемым ваттметром, показания которого определяется по формуле:

где U_w, I_w — векторы напряжения и тока, подведенные к обмоткам прибора.

Для измерения активной мощности всей трехфазной цепи в зависимости от схемы соединения фаз нагрузки и ее характера применяются различные схемы включения измерительных приборов. Для измерения активной мощности симметричной трехфазной цепи применяется схема с одним ваттметром, который включается в одну из фаз и измеряет активную мощность только этой фазы. Активная мощность всей цепи получается путем умножения показания ваттметра на число фаз: P=3W=3U_фI_фcos(φ). Схема с одним ваттметром может быть использована только для ориентированной оценки мощности и неприменима для точных и коммерческих измерений.

При отсутствии нулевого провода линейные (фазные) ток связаны между собой уравнением 1-го закона Кирхгофа: I_A+I_B+I_C=0. Сумма показаний двух ваттметров равна:

Таким образом, сумма показаний двух ваттметров равна активной трехфазной мощности, при этом показание каждого прибора в отдельности зависит не только величины нагрузки но и от ее характера.

На рис. 40.4 показана векторная диаграмма токов и напряжений для симметричной нагрузки. Из диаграммы следует, что показания отдельных ваттметров могут быть определены по формулам:

16.Переходные процессы в линейных электрических цепях, основные понятия ,законы.

Переходный процесс возникает в электрической цепи призматического режима ее работы под воздействием выключений при включении и выключении источников,потребителей либо при аварийных режимах на участках цепи(ХХ и КЗ).Переходный процесс с индуктивностью либо емкостью не может протекать мгновенно,т.к.энергия магнитного поля индуктивности или электрического поля емкости не может изменяться скачком.Любое изменение в электрической цепи вызывает изменение режима работы,наз коммутацией.

Законы коммутации:1) Ток индуктивного элемента не может изменяться скачком. Il(-0)=Il(0)=Il(+0);2)Напряжение на емкостном элементе не может изменяться скачком Uc(-0)= Uc (0)= Uc (+0)

17.Переходные процессы в электрической цепи с индуктивным элементов.(рассмотреть на примере задачи)

Электромагнит постоянного тока имеет сопротивление R=11 Ом и индуктивность L=0,44 Гн. Напряжение источника U=220 В. Рассчитать сопротивление R_p реостата, шунтирующего обмотку электромагнита, при котором напряжение на обмотке в момент отключения электромагнита не превысит утроенного значения напряжения источника.

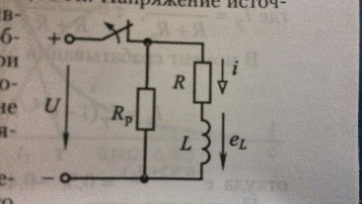
Решение. Установившееся значение тока электромагнита, включенного под напряжение, I=U/R=20 А. Электрическое состояние цепи при отключенном источнике напряжения характеризуется уравнением

Решение которого i=Ae -(R+R _p )/ L * t .

Поскольку ток в индуктивности не изменяется скачком, то в момент размыкания ключа(t=0) i(0)=20=Ae 0 , значит А=20, и ток в переходном режиме

Напряжение на обмотке электромагнита

Сопротивление R_p расчитываем так, что бы в момент отключения (t=0) u_ЭМ было больше либо равно 3U:

3U>=20 R_pe 0 ; R_p Pt P-корень 1+RCP=0

Источник

СПОСОБЫ ПОВЫШЕНИЯ КОЭФФИЦИЕНТА МОЩНОСТИ

Одной из причин низкого значения является неполная загрузка асинхронных электродвигателей, так как активная мощность определяется активной нагрузкой, тогда как реактивная зависит от общей мощности двигателя, его типа и загрузки. Следовательно, неправильный выбор типа двигателя и его мощности (с запасом) приводит к понижению значения

Важнейшим условием рационального использования электроэнергии (т. е. повышения является полная загрузка электродвигателя и недопущение его длительной работы на холостом ходу, правильный выбор типа двигателя и его мощности. Такой способ повышения называют естественным.

Если применение естественного способа не дает нужных результатов, то могут быть применены и способы искусственного повышения

Одним из наиболее распространенных способов искусственного повышения является компенсация сдвига фаз между напряжением и общим током в цепи потребителя (или группы потребителей). Например, параллельно двигателю Д подключают конденсатор (рис. 1-24). Компенсация сводится к тому, что за счет емкостного тока конденсатора уменьшается сдвиг по фазе между током и напряжением в цепи двигателя. Путем подбора емкости конденсатора С можно довести значение сдвига по фазе до нуля.

Физическая сущность явления компенсации состоит в том, что двигатель, например, в четные четверти периода запасает энергию в магнитном поле, а в нечетные — отдает ее, а конденсатор, наоборот, в нечетные четверти периода запасает энергию в электрическом поле, а в четные — отдает ее. Причем энергия, накапливаемая в магнитном поле двигателя и в электрическом поле конденсатора, является «обменной» (неиспользуемой)

энергией. Таким образом, обменная энергия будет частично или полностью «циркулировать» междумагнитным полем двигателя и электрическим полем конденсатора. При установившемся режиме работыисточник тока и линия электропередачи будут частично или полностью разгружены от «обменной» энергии.

Однако искусственные методы не позволяют в данной цепи избавиться от «обменной» энергии, они могут лишь локализовать ее, освобождая при этом сети и их станции. Практическое применение конденсаторов для компенсации несколько ограничено из-за их высокой стоимости. Поэтому на практике получили широкое распространение так называемые синхронные компенсаторы — синхронные двигатели облегченной конструкции, работающие на холостом ходу и создающие емкостный ток

Повышение коэффициента мощности в цепях синусоидального тока

Большинство современных потребителей электрической энергии имеют индуктивный характер нагрузки, токи которой отстают по фазе от напряжения источника. Так для асинхронных двигателей, трансформаторов,сварочных аппаратов и других реактивный ток необходим для создания вращающегося магнитного поля у электрических машин и переменного магнитного потока трансформаторов. Активная мощность таких потребителей при заданных значениях тока и напряжения зависит от cosφ: P = UICosφ, I = P / UCosφ Снижение коэффициента мощности приводит к увеличению тока. Косинус фи особенно сильно снижается при работе двигателей и трансформаторов вхолостую или при большой недогрузке. Если в сети есть реактивный ток мощность генератора, трансформаторных подстанции и сетей используется не полностью. С уменьшением cosφ значительно возрастают потери энергии на нагрев проводов и катушек электрических аппаратов. Например, если активная мощность остается постоянной, обеспечивается током 100 А при cosφ=1, то при понижении cosφ до 0,8 и той же мощности сила тока в сети возрастает в 1,25 раза (Iа = Iсети х cosφ, Iс = Iа / cosφ ). Потери на нагрев проводов сети и обмоток генератора (трансформатора) Pнагр = I 2 сети х Rсети пропорциональны квадрату тока, то есть они возрастают в 1,25 2 = 1,56 раза. При cosφ= 0,5 сила тока в сети при той же активной мощности равна 100 / 0,5 = 200 А, а потери в сети возрастают в 4 раза (!). Возрастают потери напряжения в сети, что нарушает нормальную работу других потребителей. Счетчик потребителя во всех случаях отсчитывает одно и то же количество потребляемой активной энергии в единицу времени, но в последнем случае генератор подает в сеть силу тока, в 2 раза большую, чем в первом. Нагрузка же генератора (тепловой режим) определяется не активной мощностью потребителей, а полной мощностью в киловольт-амперах, то есть произведением напряжения на силу тока, протекающего по обмоткам. Если обозначить сопротивление проводов линии Rл, то потери мощности в ней можно определить так: Таким образом, чем выше потребителя, тем меньше потери мощности в линии и дешевле передача электроэнергии. Коэффициент мощности показывает, как используется номинальная мощность источника. Так, для питания приемника 1000 кВт при φ= 0,5 мощность генератора должна быть S = P / cosφ = 1000 / 0,5 = 2000 кВА, а при cosφ = 1 S = 1000 кВА. Следовательно, повышение коэффициента мощности увеличивает степень использования мощности генераторов. Для повышения коэффициента мощности (cosφ) электрических установок применяют компенсацию реактивной мощности. Увеличения коэффициента мощности (уменьшения угла φ — сдвига фаз тока и напряжения) можно добиться следующими способами: 1) заменой мало загруженных двигателей двигателями меньшей мощности, 2) понижением напряжения 3) выключением двигателей и трансформаторов, работающих на холостом ходу, 4) включением в сеть специальных компенсирующих устройств, являющихся генераторами опережающего (емкостного) тока. На мощных районных подстанциях для этой цели специально устанавливают синхронные компенсаторы — синхронные перевозбужденные электродвигатели. Синхронные компенсаторы Чтобы повысить экономичность энергетических установок наиболее часто используют батареи конденсаторов, подключаемые параллельно индуктивной нагрузке (рис. 2 а). Рис. 2 Включение конденсаторов для компенсации реактивной мощности: а — схема, б, в — векторные диаграммы Для компенсации cosφ в электрических установках до нескольких сотен кВА применяют косинусные конденсаторы. Их выпускают на напряжение от 0,22 до 10 кВ. Емкость конденсатора, необходимую для повышения cosφ от существующего значения cosφ1 до требуемого cosφ2, можно определить по диаграмме (рис. 2 б, в). При построении векторной диаграммы в качестве исходного вектора принят вектор напряжения источника. Если нагрузка представляет собой индуктивный характер, то вектор тока I1 отстает от вектора напряжения на угол φ1Iа совпадает по направлению с напряжением, реактивная составляющая тока Iр отстает от него на 90° (рис. 2 б). После подключения к потребителю батареи конденсаторов ток I определяется как геометрическая сумма векторов I1 и Ic. При этом вектор емкостного тока опережает вектор напряжения на 90° (рис. 2, в). Из векторной диаграммы видно, что φ2 2 ) х (tgφ1 — tgφ2). На практике обычно коэффициент мощности повышают не до 1,0, а до 0,90 — 0,95, так как полная компенсация требует дополнительной установки конденсаторов, что часто экономически не оправдано.

Резонанс напряжений и токов в цепи переменного тока. Векторные диаграммы, частотные и энергетические характеристики. Понятие о расчете сложных (с несколькими источниками питания) цепей.

Явление резонанса. Электрическая цепь, содержащая индуктивность и емкость, может служить колебательным контуром, где возникает процесс колебаний электрической энергии, переходящей из индуктивности в емкость и обратно. В идеальном колебательном контуре эти колебания будут незатухающими. При подсоединении колебательного контура к источнику переменного тока угловая частота источника ? может оказаться равной угловой частоте ?₀, с которой происходят колебания электрической энергии в контуре. В этом случае имеет место явление резонанса, т. е. совпадения частоты свободных колебаний ?₀, возникающих в какой-либо физической системе, с частотой вынужденных колебаний ?, сообщаемых этой системе внешними силами.

Резонанс в электрической цепи можно получить тремя способами: изменяя угловую частоту ? источника переменного тока, индуктивность L или емкость С. Различают резонанс при последовательном соединении L и С — резонанс напряжений и при параллельном их соединении — резонанс токов. Угловая частота ?₀, при которой наступает резонанс, называется резонансной, или собственной частотой колебаний резонансного контура.

Резонанс напряжений. При резонансе напряжений (рис. 196, а) индуктивное сопротивление X_Lравно емкостному Х_си полное сопротивление Z становится равным активному сопротивлению R:

Z = ?( R 2 + [?₀L — 1/(?₀C)] 2 ) = R

В этом случае напряжения на индуктивности U_L и емкости U_c равны и находятся в противофазе (рис. 196,б), поэтому при сложении они компенсируют друг друга. Если активное сопротивление цепи R невелико, ток в цепи резко возрастает, так как реактивное сопротивление цепи X = X_L—X_с становится равным нулю. При этом ток I совпадает по фазе с напряжением U и I=U/R. Резкое возрастание тока в цепи при резонансе напряжений вызывает такое же возрастание напряжений U_L и U_c, причем их значения могут во много раз превышать напряжение U источника, питающего цепь.

Угловая частота ?0, при которой имеют место условия резонанса, определяется из равенства ?_oL = 1/(?₀С).

Рис. 196. Схема (а) и векторная диаграмма (б) электрической цепи, содержащей R, L и С, при резонансе напряжений

Если плавно изменять угловую частоту ? источника, то полное сопротивление Z сначала начинает уменьшаться, достигает наименьшего значения при резонансе напряжений (при ?_o), а затем увеличивается (рис. 197, а). В соответствии с этим ток I в цепи сначала возрастает, достигает наибольшего значения при резонансе, а затем уменьшается.

Резонанс токов. Резонанс токов может возникнуть при параллельном соединении индуктивности и емкости (рис. 198, а). В идеальном случае, когда в параллельных ветвях отсутствует активное сопротивление (R₁=R₂ = 0), условием резонанса токов является равенство реактивных сопротивлений ветвей, содержащих индуктивность и емкость, т. е. ?_oL = 1/(?_oC). Так как в рассматриваемом случае активная проводимость G = 0, ток в неразветвленной части
цепи при резонансе I=U?(G 2 +(B_L-B_C) 2 )= 0. Значения токов в ветвях I₁ и I₂ будут равны (рис. 198,б), но токи будут сдвинуты по фазе на 180° (ток IL в индуктивности отстает по фазе от напряжения U на 90°, а ток в емкости I с опережает напряжение U на 90°). Следовательно, такой резонансный контур представляет собой для тока I бесконечно большое сопротивление и электрическая энергия в контур от источника не поступает. В то же время внутри контура протекают токи I_L и I_с, т. е. имеет место процесс непрерывного обмена энергией внутри контура. Эта энергия переходит из индуктивности в емкость и обратно.

Как следует из формулы (74), изменяя значения емкости С или индуктивности L, можно изменять частоту колебаний ?₀ электрической энергии и тока в контуре, т. е. осуществлять настройку контура на требуемую частоту. Если бы в ветвях, в которых включены индуктивность и емкость, не было активного сопротивления, этот процесс колебания энергии продолжался бы бесконечно долго, т. е. в контуре возникли бы незатухающие колебания энергии и токов I_L и I_с. Однако реальные катушки индуктивности и конденсаторы всегда поглощают электрическую энергию (из-за наличия в катушках активного сопротивления проводов и возникновения

Рис. 197. Зависимость тока I и полного сопротивления Z от ? для последовательной (а) и параллельной (б) цепей переменного тока

Рис. 198. Электрическая схема (а) и векторные диаграммы (б и в) при резонансе токов

в конденсаторах токов смещения, нагревающих диэлектрик), поэтому в реальный контур при резонансе токов поступает от источника некоторая электрическая энергия и по неразветвленной части цепи протекает некоторый ток I.

Условием резонанса в реальном резонансном контуре, содержащем активные сопротивления R₁и R₂, будет равенство реактивных проводимостей B_L= B_Cветвей, в которые включены индуктивность и емкость.

Из рис. 198, в следует, что ток I в неразветвленной части цепи совпадает по фазе с напряжением U, так как реактивные токи 1_L и I_с равны, но противоположны по фазе, вследствие чего их векторная сумма равна нулю.

Если в рассматриваемой параллельной цепи изменять частоту ?_о источника переменного тока, то полное сопротивление цепи начинает увеличиваться, достигает наибольшего значения при резонансе, а затем уменьшается (см. рис. 197,б). В соответствии с этим ток I начинает уменьшаться, достигает наименьшего значения I_min = I_a при резонансе, а затем увеличивается.

В реальных колебательных контурах, содержащих активное сопротивление, каждое колебание тока сопровождается потерями энергии. В результате сообщенная контуру энергия довольно быстро расходуется и колебания тока постепенно затухают. Для получения незатухающих колебаний необходимо все время пополнять потери энергии в активном сопротивлении, т. е. такой контур должен быть подключен к источнику переменного тока соответствующей частоты ?₀.

Явления резонанса напряжения и тока и колебательный контур получили весьма широкое применение в радиотехнике и высокочастотных установках. При помощи колебательных контуров мы получаем токи высокой частоты в различных радиоустройствах и высокочастотных генераторах. Колебательный контур — важнейший элемент любого радиоприемника. Он обеспечивает его избирательность, т. е. способность выделять из радиосигналов с различной длиной волны (т. е. с различной частотой), посланных различными радиостанциями, сигналы определенной радиостанции.

Резонанс напряжений

Если в цепь переменного тока включены последовательно катушка индуктивности и конденсатор, то они по-своему воздействуют на генератор, питающий цепь, и на фазовые соотношения между током и напряжением.

Катушка индуктивности вносит сдвиг фаз, при котором ток отстает от напряжения на четверть периода, конденсатор же, наоборот, заставляет напряжение в цепи отставать по фазе от тока на четверть периода. Таким образом, действие индуктивного сопротивления на сдвиг фаз между током и напряжением в цепи противоположно действию емкостного сопротивления.

Это приводит к тому, что общий сдвиг фаз между током и напряжением в цепи зависит от соотношения величин индуктивного и емкостного сопротивлений.

Если величина емкостного сопротивления цепи больше индуктивного, то цепь носит емкостный характер, т. е. напряжение отстает по фазе от тока. Если же, наоборот, индуктивное сопротивление цепи больше емкостного, то напряжение опережает ток, и, следовательно, цепь носит индуктивный характер.

Общее реактивное сопротивление Хобщ рассматриваемой нами цепи определяется путем сложения индуктивного сопротивления катушки XL и емкостного сопротивления конденсатора ХС.

Но так как действие этих сопротивлений в цепи противоположно, то одному из них, а именно Хс приписывается знак минус, и общее реактивное сопротивление определяется по формуле:

Хобщ = XL -ХС, XL = ?L, ХС = 1 / ?С

Применив к этой цепи закон Ома, получим:

Формулу эту можно преобразовать следующим образом:

U = I Хобщ = I (XL -ХС) = IXL -IХС

В полученном равенстве IXL —действующее значение слагающей общего напряжения цепи, идущей на преодоление индуктивного сопротивления цепи, а IХС—действующее значение слагающей общего напряжения цепи, идущей на преодоление емкостного сопротивления.

Таким образом, общее напряжение цепи, состоящей из последовательного соединения катушки и конденсатора, можно рассматривать как состоящее из двух слагаемых, величины которых зависят от величин индуктивного и емкостного сопротивлений цепи.

Мы считали, что такая цепь не обладает активным сопротивлением. Однако в тех случаях, когда активное сопротивление цепи не настолько уже мало, чтобы им можно было пренебречь, общее сопротивление цепи определяется следующей формулой:

где R — общее активное сопротивление цепи, XL -ХС — ее общее реактивное сопротивление. Переходя к формуле закона Ома, мы вправе написать: U = I / Z

Источник