Способы построения сопряжения урок

ПЛАН-КОНСПЕКТ УРОКА ПО ЧЕРЧЕНИЮ ТЕМА: «СОПРЯЖЕНИЯ»
план-конспект урока (7 класс) по теме

ПЛАН-КОНСПЕКТ УРОКА ПО ЧЕРЧЕНИЮ ТЕМА: «СОПРЯЖЕНИЯ»

Скачать:

Вложение	Размер
doklad2.doc	126 КБ

Предварительный просмотр:

МОУ ООШ с. СЕРЕДНИКОВО

ПЛАН-КОНСПЕКТ УРОКА ПО ЧЕРЧЕНИЮ ТЕМА: «СОПРЯЖЕНИЯ»

Учитель: Кравцова Н.А.

с. Середниково 2010

Тема урока: «Сопряжения»

Цели и задачи урока: познакомить учащихся с определением сопряжения; выяснить значение сопряжений и их применение; научить выполнять графические построения плавных переходов прямых линий, прямой и кривой, кривых линий; приучать школьников эстетически воспринимать результаты своего графического труда.

Оборудование: чертежные инструменты и принадлежности, карточки задания, электронная презентация.

1. Организационный этап.
2. Повторение пройденного материала.

1. Работа у доски:

А) разделить окружность на три шесть равных частей;

Б) разделить окружность на четыре и восемь равных частей;

2. Один учащийся работает с индивидуальной карточкой: на чертеже построить проекции трех точек, грани и ребра на всех трех видах. Остальные учащиеся слушают отвечающих у доски, дополняют, исправляют.

III. Объяснение нового материала.

1 объявление целей и задач урока

2. вступительная беседа

Построение сопряжений, различных линий и других фигур с помощью циркуля

встречается часто при выполнении чертежей.

Сопряжением называется плавный переход одной линии в другую.

Применение сопряжений настолько разнообразно и многопланово, что все

примеры их использования невозможно рассмотреть. Сопряжение в технических деталях, изделиях, мебели, предметах обихода применяют для увеличения прочности, удобного и безопасного обращения, эстетики внешней формы.

3. Сейчас вы будете учиться сопрягать элементы деталей. Начнем с самого простого построения: плавного перехода двух прямых линий, пересекающихся под прямым, острым и тупым углами. Основа всех таких построений — это знание радиуса сопряжения, нахождение центра сопряжения и построение точек сопряжения (основные элементы построения сопряжения).

4. Объяснение построения сопряжений с демонстрацией на мониторе. От каждой сопрягаемой прямой проводим параллельные прямые па расстоянии, равном радиусу сопряжения (радиус сопряжения обычно известен и указан на чертеже). В точке пересечения этих прямых находится точка О — центр сопряжения. Найдем точки сопряжения. Проведем перпендикуляры из центра сопряжения к заданным прямым. Полученные точки являются точками сопряжения. Из найденного центра раствором циркуля, равным радиусу сопряжения проведем дугу, соединяющую точки сопряжения (сопрягающую дугу), она является плавным переходом одной линии в другую.

Ученики работают в тетрадях, выполняя сопряжения острого и тупого углов.

5. Сопряжение прямой линии и кривой (дуги окружности). Для нахождения центра сопряжения из точки О окружности проводят дугу вспомогательной окружности радиуса r+rl. На расстоянии rl от прямой проводят параллельную ей прямую до пересечения с дугой. Точка О1 будет точкой сопряжения. Соединив прямой точки О и О1, т.е. центры окружности и сопрягаемой дуги, получаем точку сопряжения М. Проведя из точки О1 перпендикуляр к прямой, определяют вторую точку сопряжения Н. Циркулем соединяют точки М и Н (точки сопряжения) и получают плавный переход от окружности к прямой.

6. Переход от одной окружности к другой будет плавным, если окружности касаются. Точка сопряжения находится на прямой, соединяющей их центры.

IV. Закрепление нового материала (ответы на вопросы)

1. что называют сопряжением?
2. назовите основные элементы сопряжения?
3. где применяют сопряжение?
4. каково значение сопряжений?

V. Практическая работа.

Учащиеся получают листы формата А4, где они должны построить сопряжение двух прямых линий (радиус сопряжения равен 10).

Домашнее задание Параграф 15 стр. 102 — 106, задание № 41 стр. 105.

Источник

Сопряжения

В этой небольшой статье, будут рассмотрены основные виды сопряжений и Вы узнаете о том, как построить сопряжение углов, прямых линий, окружностей и дуг, окружностей с прямой.

Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.

Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.

Ниже будут рассмотрены основные типы сопряжений.

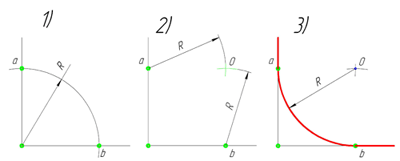
Сопряжение углов (Сопряжение пересекающихся прямых)

Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)

В данном примере будет рассмотрено построение сопряжения прямого угла заданным радиусом сопряжения R. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.

Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)

Ещё один пример сопряжения угла. В этом примере будет построено сопряжение
острого угла. Для построения сопряжения острого угла раствором циркуля,равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a
и b. Сопряжение острого угла построено.

Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)

Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.

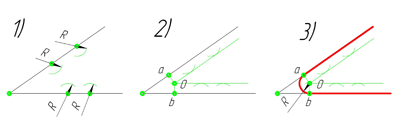
Сопряжение параллельных прямых линий

Построим сопряжение двух параллельных прямых. Нам задана точка сопряжения a, лежащая на одной прямой. Из точки a проведём перпендикуляр до пересечения его с другой прямой в точке b. Точки a и b являются точками сопряжения прямых линий. Проведя из каждой точки дугу, радиусом больш отрезка ab, найдём центр сопряжения — точку О. Из центра сопряжения проведём дугу заданного радиуса сопряжения R.

Сопряжение окружностей(дуг) с прямой линией

Внешнее сопряжение дуги и прямой линии

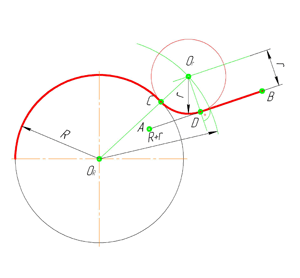
В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R.

Сначала найдём центр сопряжения. Для этого проведём прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса сопряжения r, и дугу, из центра окружности O R радиусом R+r. Точка пересечения дуги и прямой и будет центром сопряжения – точкой О r .

Из центра сопряжения, точки О r , опустим перпендикуляр на прямую AB. Точка D, полученная на пересечении перпендикуляра и отрезка AB, и будет точкой сопряжения. Найдём вторую точку сопряжения на дуге окружности. Для этого соединим центр окружности О R и центр сопряжения О r линией. Получим вторую точку сопряжения – точку C. Из центра сопряжения проведём дугу сопряжения радиусом r, соединив точки сопряжения.

Внутреннее сопряжение прямой линии с дугой

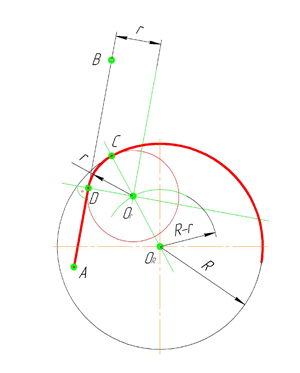
По аналогии строится внутреннее сопряжение прямой линии с дугой. Рассмотрим пример построения сопряжения радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиуса R. Найдём центр сопряжения. Для этого построим прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса r, и дугу, из центра окружности O R радиусом R-r. Точка О r , полученная на пересечении прямой и дуги, и будет центром сопряжения.

Из центра сопряжения(точка О r ) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.

Для нахождения второй точки сопряжения на дуге окружности, соединим центр сопряжения Оr и центр окружности О R прямой линией. На пересечении линии с дугой окружности получим вторую точку сопряжения – точку C. Из точки О r , центра сопряжения, проведём дугу радиусом r, соединив точки сопряжения.

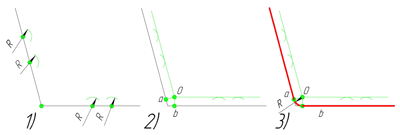
Сопряжение окружностей (дуг)

Внешнее сопряжение дуг окружностей

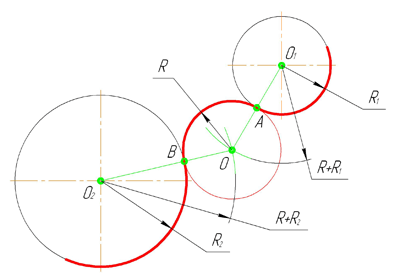
Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей(дуг) O1( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.

Внутреннее сопряжение дуг окружностей

Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.

Смешанное сопряжение дуг окружностей

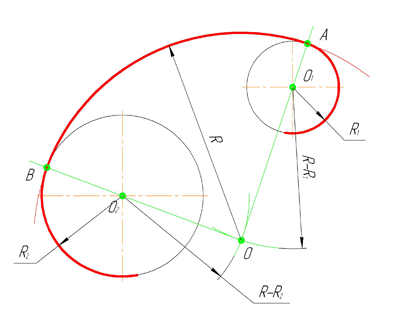
Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.

Источник

Открытый урок по черчению на тему: «Сопряжение»

МКОУ СОШ с. Карман

Открытый урок по черчению в

8 классе на тему:

Учитель ИЗО и черчения

Тема урока: Сопряжения.

— Формирование новых понятий.

— Систематизация обобщения знаний.

— Развитие творческого мышления.

— Развитие умений и навыков работы с чертежными

— Формирование качеств творческой личности.

-Интерес к народному творчеству

— Показ важности изучаемой темы.

— Показ значимости приобретенных знаний.

— Формирование умений осуществлять контроль.

— Воспитать аккуратность, четкость, самостоятельность

Оборудование для учащихся:

тетради, чертежные инструменты, карточки-задания, учебник, формат А4

для учителя: учебник, чертежные инструменты, проектор, экран, презентация с примерами по теме. Плакаты:

Чертежи плоских деталей.

Построение сопряжений прямых линий. Элементы сопряжений.

Наглядное изображение с чертежом данной детали.

Организационная часть (2 минуты)

Повторение пройденного материала (5 минут)

Изложение нового материала (20 минут)

Закрепление пройденного на уроке (15минут)

Итог урока. Задание на дом (3 минут)

Приветствие ребят. Выявление дежурных и отсутствующих.

2. Повторение пройденного материала «Геометрические построения»

Проверка творческой работы по пройденной теме.

Фронтальный опрос: (задание на карточках-«раскрасках» с заранее вычерченными окружностями)

1-й вариант — задание: разделить окружность на 4 равных части;

2-й вариант — разделить окружность на 3 равные частей.

Сдача работ 1 и 2-го варианта и проверка чертежей через изображения на мониторе.

Демонстрируются наиболее яркие и простые примеры использования сопряжений в технике, архитектуре, дизайне и т.д.

Затем сами школьники приводят аналогичные примеры из их быта и жизненного опыта.

3. Изложение нового материала

Сегодня на уроке мы познакомимся с сопряжениями линий.

На карточках даны детали, рассмотрите их и дайте ответы на вопросы.

— Сравните форму данных деталей и скажите, чем они отличаются друг от друга?

— Посмотрите на чертежи подобных деталей и скажите, чем они отличаются друг от друга?

— Какое из этих изображений вы могли бы построить прямо сейчас?

— При помощи какого чертежного инструмента можно построить округления углов?

Плавные переходы линий встречаются при моделировании одежды, когда строится выкройка; в чертежах деталей, в орнаментах различных народов; в украшениях и т.д.

Плавный переход одной линии в другую называется сопряжением .

Где применяется сопряжение?

Сопряжение применяется для того, чтобы построить контур технической детали, (показ двух технических деталей), где можно наблюдать плавные переходы одной поверхности в другую. Для того чтобы построить чертежи данных деталей, необходимо знать способы построения сопряжений. Плавные переходы одной поверхности в другую на технических деталях применяются для того, чтобы повысить стойкость и увеличить прочность.

Плавные переходы одной поверхности в другую применяют в эстетических целях. (Показ предметов с красивыми контурными линиями).

Говоря о красоте плавных линий, нельзя не сказать о том, что они применяются в архитектуре.

Я думаю, что убедила вас в том, что знание способов построения сопряжений линий необходимо.

Сначала мы рассмотрим сопряжение прямых линий, когда они располагаются под прямым углом, под острым углом и под тупым углом.

Рассмотрим элементы сопряжений на примере построения сопряжения тупого угла, причем стороны угла называются сопрягаемыми линиями.

Радиус сопряжений R

Центр сопряжений т. О

Точки сопряжений т. А и т. В

Центр (т. О) лежит на пересечении прямых, которые параллельны сопрягаемым линиям и находятся на расстоянии равном радиусу дуги сопряжения. Затем находим точки сопряжения. Они лежат на пересечении перпендикуляров проведенных из центра дуги сопряжения к сопрягаемым линиям. Затем опорную ножку циркуля ставим в центр и проводим дугу сопряжения плавно соединяя т. А с т. В.

Какие элементы сопряжения необходимо знать, чтобы построить дугу сопряжения?

Показать построение сопряжения острого угла на доске (учащиеся данную работу выполняют в тетрадях).

При построении напомнить о типах линий. После того, как построение закончено чертеж обвести основной сплошной толстой линией, начиная с дуги сопряжения. Теперь давайте, выполним построение сопряжения тупого угла. Один ученик данную работу делает у доски, остальные в тетрадях.

Сопряжение прямой и окружности дугой заданного радиуса.

Рассмотрим это на примере построения фронтальной проекции детали «Опора» Будем считать, что большая часть построения проекции уже сделана; необходимо отобразить плавный переход цилиндрической части поверхности к плоской. Для этого необходимо выполнить сопряжение окружности (дуги окружности) с прямой линией заданным радиусом:

1.найдем центры сопряжения как точки пересечения четырех вспомогательных линий: двух прямых, параллельных верхнему ребру основания «Опоры

и удаленных от нее на расстояние, равное радиусу сопряжения, и двух вспомогательных дуг, отстоящих от заданной дуги (цилиндрической поверхности) «Опоры» на расстояние, равное радиусу сопряжения;

2. найдем точки сопряжения как точки пересечения: а) заданных прямых (ребер «Опоры») с перпендикулярами, опущенными к ним из центров сопряжения; б) заданной дуги, изображающей на чертеже цилиндрическую поверхность опоры, с прямыми, соединяющими центры сопряжения с центром сопрягаемой дуги;

3. из центров сопряжения проводим дуги радиусом сопряжения от одной точки сопряжения до другой. Обводим изображение.

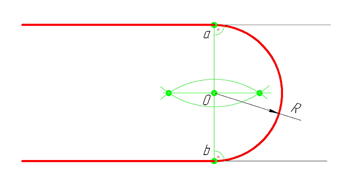
Сопряжение дуг окружностей дугами заданного радиуса.

Рассмотрим это на примере построения фронтальной проекции формы для выпечки печенья, имеющей плавные переходы одной поверхности в другую:

1. проведем вертикальную и горизонтальные осевые линии. На них найдем центры и проведем три дуги радиусом R;

2. найдем центр сопряжения двух верхних окружностей как точку пересечения вспомогательных дуг радиусами, равными сумме радиусов заданной окружности (R) и сопряжения (R ₁ ), т. е. R + R ₁ ;

3. найдем точки сопряжения как точки пересечения заданных окружностей с прямыми, соединяющими центр сопряжения с центрами окружностей. Такое сопряжение называют внешним сопряжением;

4. построим сопряжения двух окружностей дугой заданного радиуса сопряжения R ₂ • Сначала найдем центр сопряжения пересечением дуг вспомогательных окружностей, радиусы которых равны разности радиуса сопряжения R ₂ и радиуса окружности R, т. е. R ₂ — R. Точки сопряжения получены на пересечении окружности с продолжением линии, соединяющей центр сопряжения с центром окружности. Из центра сопряжения проведем дугу радиусом R ₂ • Такое сопряжение называется внутренним сопряжением;

5. аналогичные построения выполним с другой стороны от оси симметрии.

Источник