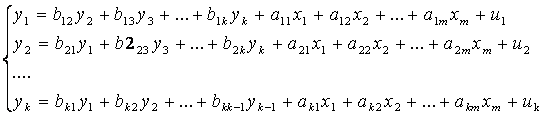Способы построения систем эконометрических уравнений

Системы эконометрических уравнений

Вы будете перенаправлены на Автор24

Характеристика систем независимых и одновременных уравнений

В социальных науках в последнее время всё активнее применяются методы статистических исследований, объектом которых выступают сложные системы. Для того, чтобы дать описание и объяснение механизма их функционирования, недостаточно построить изолированные уравнения регрессии. Как правило, изменение одной переменной сопровождается изменением других переменных.

Отсюда следует, что особо значима проблема описания структуры связей между переменными, которая может быть решена применением системы уравнений. Например, если объектом исследования является спрос, который рассматривается как отношение количества потребляемых товаров и цен на них, в то же время требуется изучить предложение этих товаров. Благодаря этому можно определить искомое равновесное состояние на рынке.

Существуют два основных способа построения системы уравнений.

В самом общем виде система независимых уравнений, где каждая зависимая переменная Y рассматривается как функция одного и того же набора факторов Х, записывается на эконометрическом языке следующим образом:

Рисунок 1. Система независимых уравнений. Автор24 — интернет-биржа студенческих работ

В каждом уравнении, рассматриваемом в самостоятельном порядке, набор факторов Х может варьироваться. Решение этой системы сводится к определению конкретных значений параметров А. Для этого используется широко известный метод наименьших квадратов (МНК), поскольку каждое уравнение этой системы является уравнением регрессии.

Однако этот метод не применим в отношении системы, так называемых, одновременных (совместных, взаимозависимых) уравнений, которая предполагает разное расположение зависимых переменных (в одних уравнениях – в левой части, в других уравнениях – в правой части).

Готовые работы на аналогичную тему

Рисунок 2. Система одновременных уравнений. Автор24 — интернет-биржа студенческих работ

Подобную систему уравнений в эконометрической науке зачастую называют структурной формой модели. Каждое из её уравнений не может рассматриваться самостоятельно, а для нахождения их параметров используются специальные методы оценивания.

Описание структурной и приведенной форм эконометрической модели

Структурная форма модели (то есть система одновременных уравнений) включает в себя две категории переменных:

• эндогенные (внутренние) переменные, представляющие собой зависимые переменные, которые обозначаются в математической записи как Y, а их число равняется числу уравнений в системе;
• экзогенные (внешние) переменные, представляющие собой предопределенные переменные, которые оказывают непосредственное влияние на эндогенные переменные, но каким-либо образом не зависят от них, а обозначаются в математической записи как Х.

Самая простая структурная форма модели включает в себя два уравнения: первое – Y1 = B12 ⋅ Y2 + A11 ⋅ X1 + E1, второе – Y2 = B21 ⋅ Y1 + A22 ⋅ X2 + E2. В этой системе уравнений эндогенными переменными являются Y1 и Y2, а экзогенными – Х1 и Х2, а Е1 и Е2 – это свободные члены.

Представленное деление переменных на эндогенные и экзогенные определяется, прежде всего, конкретными аспектами теоретической концепции принятой модели. Так, в одних моделях экономические переменные могут быть рассмотрены в качестве эндогенных переменных, а уже в других – в качестве экзогенных. Экзогенными переменными всегда признаются внеэкономические переменные (например, территориальная удаленность).

Кроме того, эндогенные переменные, характеризующие текущий период, в последующем периоде уже могут использоваться в качестве экзогенных переменных. Например, объем потребления в текущем периоде, помимо прочего, определяется объемами потребления в прошлых годах.

На значения эндогенной переменной оказывает влияние изменение любой экзогенной переменной, что возможно увидеть благодаря структурной формы модели. Она также предоставляет возможность получить целевые значения эндогенных переменных, потому что исследователь может выбрать, изменить и управлять экзогенными переменными (лучше через них выражать объекты регулирования).

В системе одновременных уравнений выделяют такие элементы, как структурные коэффициенты. Коэффициенты при экзогенных переменных обозначаются как А, коэффициенты при эндогенных переменных – как В.

Также имеют место быть свободные члены. Ими обозначаются не учитываемые отклонения теоретически рассчитанных переменных от фактически существующих параметров.

Структурные коэффициенты модели оцениваются посредством применения метода наименьших квадратов. Однако этот метод в результате даёт смещенные и несостоятельные оценки. Чтобы нивелировать это, в эконометрике предлагают преобразовать структурную форму модели в приведенную.

Она предполагает, что система одновременных уравнений будет преобразована в систему независимых уравнений посредством перенесения всех эндогенных переменных в левую часть уравнений, а экзогенных – в правую часть. Тогда уже применение метода наименьших квадратов становится возможным: значения эндогенных переменных могут быть выражены через экзогенные. Однако приведенная форма модели с аналитической точки зрения уступает структурной форме, поскольку в ней не оценивается взаимосвязь между эндогенными переменными.

Для структурной модели существует возможность получения единственно возможного решения. Для этого нужно уменьшить число структурных коэффициентов благодаря приравниванию некоторых из них нулю.

Источник

Системы эконометрических уравнений

Пример . Рассмотрим модель зависимости общей величины расходов на питание от располагаемого личного дохода (х) и цены продуктов питания (р):у = а₀ + а₁х + а₂р + ε. Определим класс модели и вид переменных модели: регрессионная модель с одним уравнением; эндогенная переменная — расходы на питание, экзогенные переменные — располагаемый личный доход и цена продуктов питания.

Принципиальные сложности применения систем эконометрических уравнений связаны с ошибками спецификации модели.

Система уравнений в эконометрических исследованиях может быть построена по-разному. Выделяют следующие 3 вида систем уравнений.

1. Система независимых уравнений, когда каждая зависимая переменная (y ) рассматривается как функция только от предопределенных переменных (х):
   
2. Система рекурсивных уравнений, когда в каждом последующем уравнении системы зависимая переменная представляет функцию от зависимых и предопределенных переменных предшествующих уравнений:

От структурной формы легко перейти к так называемой приведенной форме модели. Число уравнений в приведенной форме равно числу эндогенных переменных модели. В каждом уравнении приведенной формы эндогенная переменная выражается через все предопределенные переменные модели:

Так как правая часть каждого из уравнений приведенной формы содержит только предопределенные переменные и остатки, а левая часть только одну из эндогенных переменных, то такая система является системой независимых уравнений. Поэтому параметры каждого из уравнений системы в приведенной форме можно определить независимо обычным МНК.
Зная оценки этих приведенных коэффициентов можно определить параметры структурной формы модели. Но не всегда, а только если модель является идентифицируемой.

Проблема идентификации

Количество структурных и приведенных коэффициентов одинаково в модели идентифицируемой.

Правила идентификации

Ранг данной матрицы равен 1, что меньше К-1=2, следовательно, 1-ое уравнение модели неидентифицированно.
Составим матрицу А для 2-ого уравнения системы. Во 2-ом уравнении отсутствуют переменные y₃, x₂, х₃:
y₃ x ₂ x₃
b₁₃ a ₁₃ 0 — в 1-ом уравнении
1 a₃₂ a₃₃ — в 3-ем уравнении
Ранг данной матрицы равен 2, что равно К-1=2, следовательно, 2-ое уравнение модели точно идентифицированно.
Составим матрицу А для 3-его уравнения системы. В 3-ем уравнении отсутствуют переменные y₁, x₂:
y ₁ x ₂
1 a₁₂ — в 1-ом уравнении
b₂₁ 0 — во 2-ом уравнении
Ранг данной матрицы равен 1, что меньше К-1=2, следовательно, 3-е уравнение модели неидентифицированно.

Сделаем выводы: 1-ое и 3-е уравнения системы неидентифицированны (т.к. не выполняются достаточные условия идентификации, а в случае 1-ого уравнения и необходимое условие также). 2-ое уравнение системы сверхидентифицированно. Следовательно, система в целом является неидентифицируемой.
Для оценки параметров 2-ого уравнения можно применить двухшаговый МНК. Параметры 1-ого и 3-его уравнений определить по коэффициентам приведенной формы нельзя. Поэтому модель должна быть модифицирована.

Источник

Тема 10. Системы эконометрических уравнений

10.1. Общее понятие о системах уравнений, используемых в эконометрике

Объектом статистического изучения в социальных науках являются сложные системы. Построение изолированных уравнений регрессии недостаточно для описания таких систем и объяснения механизма их функционирования.

Поэтому при моделировании экономических ситуаций часто необходимо построение систем уравнений, когда одни и те же переменные могут выступать и в роли объясняющих и в роли объясняемых. Так, если изучается модель спроса как отношение цен и количества потребляемых товаров, то одновременно для прогнозирования спроса необходима модель предложения товаров, в которой рассматривается также взаимосвязь между количеством и ценой предлагаемых благ. Это позволяет достичь равновесия между спросом и предложением.

Система уравнений в эконометрических исследованиях может быть построена по-разному.

Системы уравнений здесь могут быть построены по-разному.

Возможна система независимых уравнений, когда каждая зависимая переменная y рассматривается как функция одного и того же набора факторов x:

(1)

Набор факторов x_j в каждом уравнении может варьироваться.

Каждое уравнение системы независимых уравнений может рассматриваться самостоятельно. Для нахождения его параметров используется МНК. По существу, каждое уравнение этой системы является уравнением регрессии.

Если зависимая переменная одного уравнения выступает в виде факторав другом уравнении, то исследователь может строить модель в видесистемы рекурсивных уравнений:

(2)

В данной системе зависимая переменная включает в каждое последующее уравнение в качестве факторов все зависимые переменные предшествующих уравнений наряду с набором факторов. Каждое уравнение этой системы может рассматриваться самостоятельно, и его параметры определяются методом наименьших квадратов (МНК).

Наибольшее распространение в эконометрических исследованиях получила система взаимозависимых уравнений. В ней одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других уравнениях – в правую часть системы:

(3)

Система взаимозависимых уравнений получила название системы совместных, одновременных уравнений. Тем самым подчеркивается, что в системе одни и те же переменные одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других. В эконометрике эта система уравнений называется также структурной формой модели.

В отличие от предыдущих систем каждое уравнение системы одновременных уравнений не может рассматриваться самостоятельно, и для нахождения его параметров традиционный МНК неприменим. С этой целью используются специальные приемы оценивания.

10.2. Структурная и приведенная формы модели

Экономическая модель как система одновременных уравнений может быть представлена в структурной или приведённой форме. В структурной форме её уравнения имеют исходный вид, отражая непосредственную связь между переменными.

Структурная форма модели обычно содержит эндогенные и экзогенные переменные.

Эндогенные переменные (внутренние) – это зависимые переменные, число которых равно числу уравнений в системе. Они обозначаются через y.

Экзогенные переменные (внешние) – это предопределенные переменные (задаваемые извне, независимые), влияющие на эндогенные переменные. Они обозначаются через x.

Классификация переменных на эндогенные и экзогенные зависит от теоретической концепции принятой модели. Экономические переменные могут выступать в одних моделях как эндогенные, а в других – как экзогенные переменные. Внеэкономические переменные (например, климатические условия) входят в систему как экзогенные переменные. В качестве экзогенных переменных можно рассматривать значения эндогенных переменных за предшествующий период времени (лаговые переменные). Например, потребление текущего года y_t может зависеть также и от уровня потребления в предыдущем году y_t-1.

Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной. Целесообразно в качестве экзогенных переменных выбирать такие переменные, которые могут быть объектом регулирования. Меняя их и управляя ими, можно заранее иметь целевые значения эндогенных переменных.

Простейшая структурная форма модели имеет вид:

(4)

Коэффициенты при эндогенных и – при экзогенных переменных называются структурными коэффициентами модели. Все переменные в модели выражены в отклонениях иот среднего уровня, поэтому свободный член в каждом уравнении отсутствует.

Использование МНК для оценивания структурных коэффициентов модели дает смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма преобразуется в приведенную.

Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:

(5)

коэффициенты приведенной формы модели.

По своему виду приведенная форма модели ничем не отличается от системы независимых уравнений. Применяя МНК, можно оценить , а затем оценить значения эндогенных переменных через экзогенные.

Коэффициенты приведённой формы представляют собой нелинейные функции коэффициентов структурной формы модели.

Рассмотрим это положение на примере простейшей структурной модели, выразив коэффициенты приведенной формы модели через коэффициенты структурной модели.

Для структурной модели вида (4) приведенная форма модели имеет вид

(6)

Из первого уравнения (4) можно выразить следующим образом (ради упрощения опускаем случайную величину):.

Подставляя во второе уравнение (4), имеем ,

Откуда .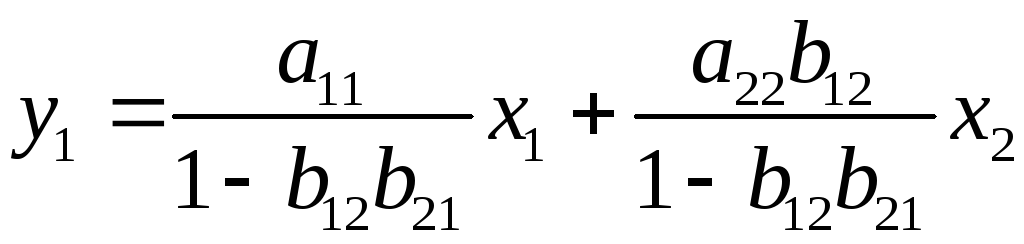

Аналогично выразим из второго уравнения системы (4) и подставив в первое, получим:.

Т.о. система (4) принимает вид:

Таким образом, можно сделать вывод о том, что коэффициенты приведенной формы модели (6) будут выражаться через коэффициенты структурной формы следующим образом:

Следует заметить, что приведенная форма модели хотя и позволяет получить значения эндогенной переменной через значения экзогенных переменных, но аналитически она уступает структурной форме модели, так как в ней отсутствуют оценки взаимосвязи между эндогенными переменными.

Источник