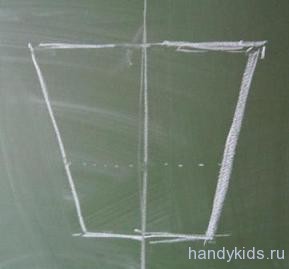Способы построения симметричной фигуры

Как изобразить симметричный предмет 2.

Мы с вами уже разобрали способы построения симметричных фигур. Вспомним: на глаз (наиболее творческий но сложный) или с помощью линейки. Можно ещё отмеряя карандашом — этот способ наименее удачный, хуже только мерить пальцами.

Сегодня начнём с дорисовывания симметричного узора.

Как действовать будем? Сначала пусть на-глазок.

И сейчас расскажу вам про ещё один простой, но эффективный способ измерения. Если узор у нас слишком сложный, проверим свой глазомер с помощью полоски бумаги, которая заменит нам сегодня линейку. Размеры различных деталей мы можем отмечать, делая засечки!

Отметили длину детали и далее сравним с нашими предварительными набросками:

Ну,что я вижу: точка, нарисованная на-глазок оказывается чуть-чуть не на месте. Что ж, придётся передвинуть — в соответствии с более точными измерениями.

Продолжим проверку точности:

Отличный, хорошо проверенный способ когда нет линейки.

Что ж, вполне похоже получилось. Узорчик что надо.

Ладно, теперь ещё применим наши уменья и навыки для построения симметричных фигур на доске. Дело это посложнее будет из-за крупных размеров.

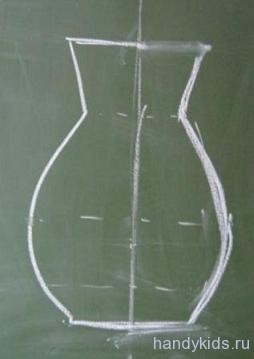
Условное ведро нарисовали. Усложним задачу. Дано: половина крынки.

Я старалась. И, нарисовав, оценивала результаты и рассматривая вблизи и издали. Но, вот ведь, не стоит быть слишком самоуверенной — на фотографии видно, что крыночка слегка завалилась. Ладно, я не упираюсь — важно уметь признать свои ошибки и избегать повторения впредь.

Как нарисовать симметричный предмет или фигуру вам рассказала Марина Новикова.

Уменье правильно рисовать симметричные предметы нам много раз пригодится. Например:

Источник

Осевая и центральная симметрии. Проводим урок с ЭФУ

Повторение материала

Из курса математики 5 класса учащиеся уже узнали, как выглядят и строятся фигуры, имеющие ось симметрии. Перед изучением темы «Осевая и центральная симметрии» будет целесообразно повторить материал 5 класса. Следует разъяснить учащимся, что построение фигуры во многих случаях возможно по положению ключевых точек.

Для закрепления этого интуитивно-наглядного понимания, учитель может предложить детям перегнуть лист бумаги, на котором изображены симметричные фигуры.

.

Понятие симметрии

Слово «симметрия» происходит от греческого symmetria, что означает соразмерность. В нашем случае, симметрия — это свойство геометрических фигур к отображению.

Учитель: Симметрия используется в рисунках, орнаментах, архитектуре с давних времен. Где еще симметрию могут использовать люди?
Ученики: при строительстве домов; в изготовлении предметов быта.
Учитель: верно, но ведь симметрия распространена не только там, где творил человек! Мы видим симметричные объекты природы каждый день. Назовите мне три таких объекта!
Ученики: Бабочка, цветы, форма листа! Морская звезда, снежинка, яблоко в разрезе.

Симметрий, как это не покажется вам странным и любопытным, много, но мы будем рассматривать две симметрии на плоскости: относительно точки и прямой.

Осевая симметрия

Осевая симметрия — это симметрия относительно проведённой прямой (оси).

Заметим, что любые две фигуры, симметричные относительно некоторой прямой, равны (Рис.131). Все точки фигуры, имеющей ось симметрии, не принадлежащие этой оси, можно разделить на пары симметричных точек (Рис. 132).

Центральная симметрия

Симметрию относительно точки называют центральной симметрией.

Фигуры, имеющие центр симметрии — понятие, воспринимающееся учащимися сложнее, чем фигуры, имеющие ось симметрии. Для удобства восприятия и понимания, рекомендуется привести как можно больше примеров из окружающей природы.

В зависимости от уровня математической подготовки учащихся класса, можно обратить их внимание на то, что прямая — это фигура, имеющая бесконечно много осей и центров симметрии.

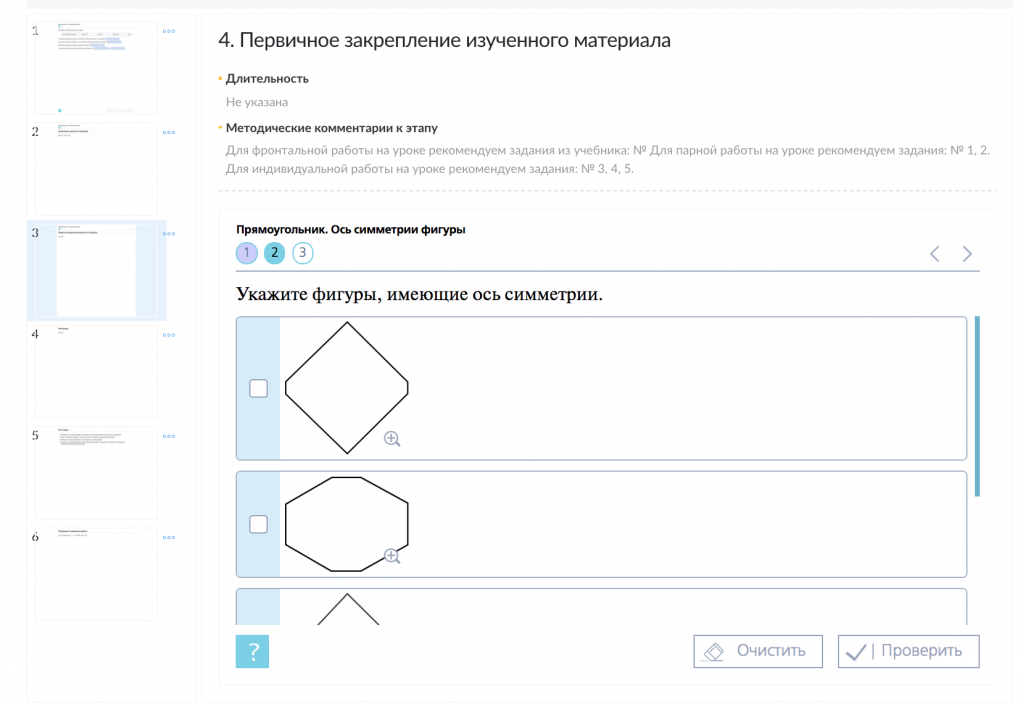
С помощью заданий из «Классной работы» материал можно закрепить в различных графических форматах.

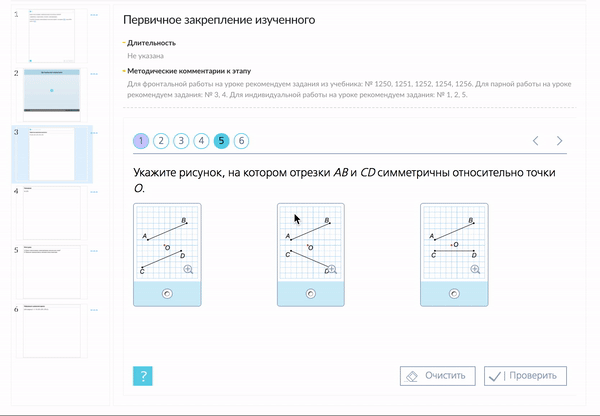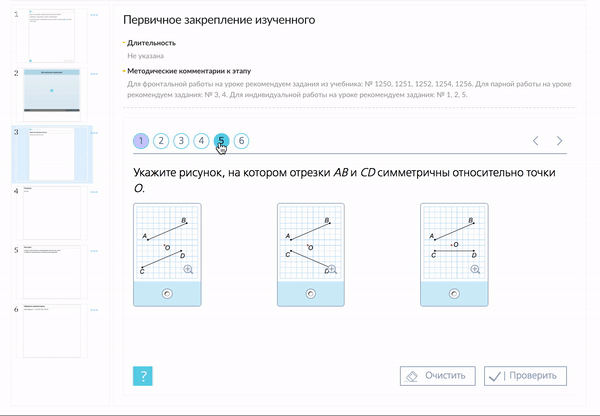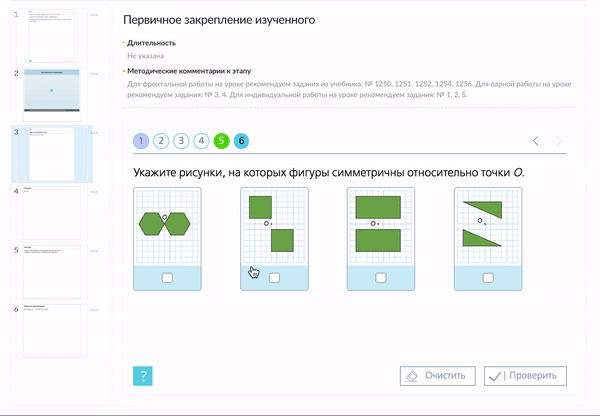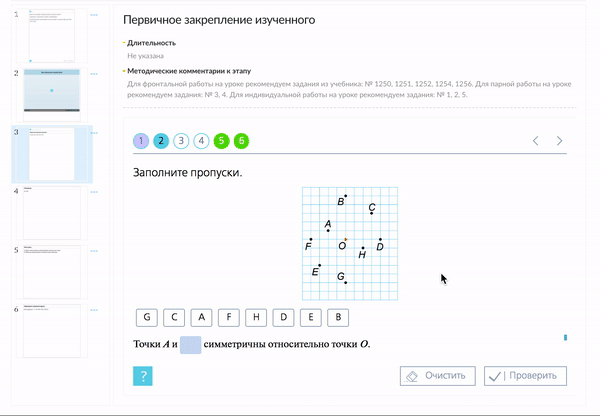
Актуализация знаний

Предложите ребятам решить задание № 1260. Какие печатные буквы русского алфавита имеют 1) вертикальную ось симметрии; 2) горизонтальную ось симметрии; 3) горизонтальную и вертикальную оси?

Готовый яркий раздаточный материал «Алфавит» вы можете скачать в конце этой статьи.

Также рекомендуем вам применять на уроке различные методы преподнесения информации: как визуальный, так и аудио. Попробуйте аудиодиктант.

Источник

Геометрия. 8 класс

Конспект
Рассмотрим прямую a и точку, не принадлежащую ей.

Точки А и А₁ называются симметричными относительно прямой а, если:
— эта прямая проходит через середину отрезка АА₁
— а ⊥ АА₁.
Прямая a называется осью симметрии. Если точка принадлежит прямой а, то она симметрична сама себе.
Составим алгоритм построения точки, симметричной данной.
Алгоритм построения
• Провести прямую b перпендикулярную прямой а
• Отложить от точки О на прямой b расстояние, равное ОА
• Получить точку А₁

Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры.

(Цвет линий и букв черный)
Равносторонний треугольник имеет три оси симметрии. Неразвернутый угол имеет одну ось симметрии – прямую, содержащую биссектрису угла.

Подумайте, какие из данных фигур имеют ось симметрии и сколько?
Рассмотрим симметрию относительно точки.
Симметрия относительно точки
Две точки А и А₁ называются симметричными относительно точки О, если О – середина отрезка АА₁.

Составим алгоритм построения точки, симметричной данной относительно точки О.
Алгоритм построения
• Соединить точку А и точку О прямой и продолжить прямую за точку О
• От точки О отложить расстояние равное ОА
• Получить точку А₁

Фигура называется симметричной относительно центра, если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре.

Центр симметрии имеет круг, квадрат.

Подумайте, какие из данных фигур имеют центр симметрии?

Слово «симметрия» греческое (συμμετρία), оно означает «соразмерность, пропорциональность, одинаковость в расположении частей», неизменность при каких-либо преобразованиях.
В словаре С.И. Ожегова симметрия – это соразмерность, пропорциональность частей чего-нибудь, расположенных по обе стороны от середины, центра.
С симметрией мы часто встречаемся в природе, архитектуре, искусстве, технике и быту. Симметрия в одежде – это символ строгости. Симметрия в архитектуре – это признак красоты и надежности. Некоторые люди утверждают, что симметрия – это совершенство.
Симметрией обладают некоторые буквы латинского и русского алфавита. Например, буква М обладает осевой симметрией, а буква Х – центральной симметрией.
Многие дорожные знаки обладают осевой или центральной симметрией. Гуляя по городу, приглядитесь к знакам. Найдите такие, которые имеют несколько осей симметрии и такие, которые не имеют осей симметрии.

Есть ось симметрии, центра симметрии нет Есть центр симметрии и 4 оси симметрии
Геометрия, 7-9: учеб. для общеобразоват. учреждений/ [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. – М.: Просвещение, 2017.

Источник

Презентация к уроку геометрии на тему «Построение симметричных фигур» (8 класс)

Описание презентации по отдельным слайдам:

Урок геометрии по теме: Построение симметричных фигур для обучающихся 8 класса с интеллектуальными нарушениями МКОУ «Школа-интернат № 66» Разработала: учитель высшей категории МКОУ «Школа-интернат № 66» Вельдяскина О.С.

Начинаем ровно в срок, Наш любимейший урок. Дружно за руки возьмёмся, И друг другу улыбнёмся.

Наш урок сейчас Науке посвящается Что геометрией у нас С любовью называется. Она поможет воспитать Такую точность мысли, Чтоб в нашей жизни всё построить, измерить и исчислить.

«Ты пришёл сюда учиться Не лениться, а трудиться, Только тот, кто много знает В жизни что–то достигает» Помни каждый ученик:

Домашняя работа № 303

Сосчитай геометрические фигуры

Какую фигуру называют симметричной относительно прямой?

Сколько осей симметрии имеют фигуры: Равнобедренный треугольник Прямоугольник Квадрат Равносторонний треугольник Окружность

Какую фигуру называют симметричной относительно точки (центра)?

Имеют ли буквы русского алфавита ось симметрии? А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н, О, П, Р, С, Т, У, Ф, Х, Ц, Ч, Ш, Щ, Ь, Ы, Ъ, Э, Ю, Я Две оси симметрии Одна ось симметрии Не имеют оси симметрии

В архитектуре В искусстве В природе Осевая и центральная симметрия

Найдите на рисунке три слова, относящиеся к уроку геометрии. Слова могут быть расположены вертикально или горизонтально. Обведи их. Составь из этих слов предложение. Назовите его.

Найдите на рисунке три слова, относящиеся к уроку геометрии. Слова могут быть расположены вертикально или горизонтально. Обведи их. Составь из этих слов предложение. Назовите его.

08.02 Классная работа Построение симметричных фигур.

Физминутка Мы все вместе улыбнемся, Подмигнем слегка друг другу, Вправо, влево повернемся (повороты влево-вправо) И кивнем затем по кругу. (наклоны влево-вправо) Все идеи победили, Вверх взметнулись наши руки. (поднимают руки вверх- вниз) Груз забот с себя стряхнули И продолжим путь науки. (встряхнули кистями рук)

Алгоритм построения симметричных точек относительно центра симметрии Алгоритм построения симметричных точек относительно оси симметрии 1. Построитьперпендикуляр от данной точки к оси симметрии. 2. Продолжитьперпендикуляр на противоположную (другую) сторону от оси симметрии. 3. Измеритьрасстояние от данной точки до пересечения перпендикуляра с осью симметрии. 4.Отмеритьполученное расстояние на продолжении перпендикуляра. 5. Поставитьточку, обозначить ее соответствующей буквой с индексом. 1. Построитьотрезок от данной точки к центру симметрии. 2. Продолжитьотрезок на противоположную (другую) сторону от центра симметрии. 3. Измеритьрасстояние от данной точки до центра симметрии. 4.Отмеритьполученное расстояние на продолжении отрезка. 5. Поставитьточку, обозначить ее соответствующей буквой с индексом.

08.02 Классная работа Построение симметричных фигур. Стр. 144 № 304

08.02 Классная работа Построение симметричных фигур. Стр. 146 № 308

Самостоятельная работа Задание: На нелинованном листе бумаге постройте симметричные фигуры.

Домашнее задание Стр. 144 № 305 Стр. 147 № 310(а)

Итог урока — Назовите тему работы на уроке. — Что мы вспомнили, повторили на уроке? — Чему мы научились на уроке? — Какие математические правила нам помогали на уроке?

ОЦЕНИ СВОЮ РАБОТУ НА УРОКЕ: -Я работал(а) отлично, в полную силу своих возможностей, чувствовал(а) себя уверенно. — Я работал(а) хорошо, но не в полную силу, испытывал(а) чувство неуверенности, боязни, что отвечу неправильно. — У меня не было желания работать. Сегодня не мой день.

Спасибо за работу на уроке!

Ищем педагогов в команду «Инфоурок»

Презентация к уроку геометрии для обучающихся 8 класса с интеллектуальными нарушениями на тему «Построение симметричных фигур». Презентация непосредственно разработана к уроку повторения учащимися темы «Построение симметричных фигур» . Урок строится на основе работы с тетрадью на печатной основе, входящей в УМК «Математика 8 класс» авторов В.В.Эк и Т.В. Алышевой.

Номер материала: ДБ-639666

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Руководители управлений образования ДФО пройдут переобучение в Москве

Время чтения: 1 минута

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

Вопрос о QR-кодах для сотрудников школ пока не обсуждается

Время чтения: 2 минуты

Российский совет олимпиад школьников намерен усилить требования к олимпиадам

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник