Способы построения сечений пирамиды

Узнать ещё

Знание — сила. Познавательная информация

Как построить сечение пирамиды

Разберем, как построить сечение пирамиды, на конкретных примерах. Поскольку в пирамиде нет параллельных плоскостей, построение линии пересечения (следа) секущей плоскости с плоскостью грани чаще всего предполагает проведение прямой через две точки, лежащие в плоскости этой грани.

В простейших задачах требуется построить сечение пирамиды плоскостью, проходящей через данные точки, уже лежащие в одной грани.

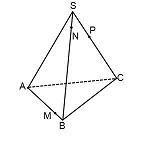
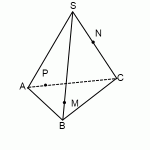
Построить сечение плоскостью (MNP)

Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.

Треугольник MNP — сечение пирамиды

Точки M и N лежат в одной плоскости ABS, следовательно, через них можем провести прямую. След этой прямой — отрезок MN. Он видимый, значит, соединяем M и N сплошной линией.

Точки M и P лежат в одной плоскости ACS, поэтому через них проведем прямую. След — отрезок MP. Мы его не видим, поэтому отрезок MP проводим штрихом. Аналогично строим след PN.

Треугольник MNP — искомое сечение.

Если точка, через которую требуется провести сечение, лежит не на ребре, а на грани, то она не будет концом следа-отрезка.

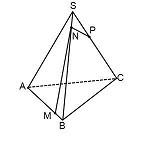
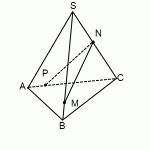
Пример. Построить сечение пирамиды плоскостью, проходящей через точки B, M и N, где точки M и N принадлежат, соответственно, граням ABS и BCS.

Здесь точки B и M лежат в одной грани ABS, поэтому можем через них провести прямую.

Аналогично проводим прямую через точки B и P. Получили, соответственно, следы BK и BL.

Точки K и L лежат в одной грани ACS, поэтому через них можем провести прямую. Ее след — отрезок KL.

Треугольник BKL — искомое сечение.

Однако не всегда через данные в условии точки удается провести прямую. В этом случае нужно найти точку, лежащую на прямой пересечения плоскостей, содержащих грани.

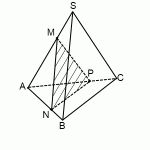
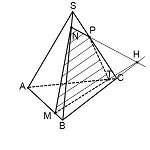
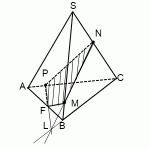
Пример. Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.

Точки M и N лежат в одной плоскость ABS, поэтому через них можно провести прямую. Получаем след MN. Аналогично — NP. Оба следа видимые, поэтому соединяем их сплошной линией.

Точки M и P лежат в разных плоскостях. Поэтому соединить их прямой не можем.

Продолжим прямую NP.

Она лежит в плоскости грани BCS. NP пересекается только с прямыми, лежащими в этой же плоскости. Таких прямых у нас три: BS, CS и BC. С прямыми BS и CS уже есть точки пересечения — это как раз N и P. Значит, ищем пересечение NP с прямой BC.

Точку пересечения (назовем ее H), получаем, продолжая прямые NP и BC до пересечения.

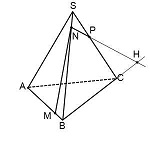
Эта точка H принадлежит как плоскости (BCS), поскольку лежит на прямой NP, так и плоскости (ABC), поскольку лежит на прямой BC.

Таким образом мы получили еще одну точку секущей плоскости, лежащей в плоскости (ABC).

Через H и точку M, лежащую в этой же плоскости, можем провести прямую.

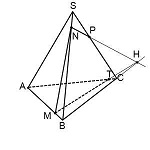
Получим след MT.

T — точка пересечения прямых MH и AC.

Так как T принадлежит прямой AC, то через нее и точку P можем провести прямую, так как они обе лежат в одной плоскости (ACS).

4-угольник MNPT — искомое сечение пирамиды плоскостью, проходящей через данные точки M,N,P.

Мы работали с прямой NP, продлевая ее для отыскания точки пересечения секущей плоскости с плоскостью (ABC). Если работать с прямой MN, приходим к тому же результату.

Рассуждаем так: прямая MN лежит в плоскости (ABS), поэтому пересекаться может только с прямыми, лежащими в этой же плоскости. У нас таких прямых три: AB, BS и AS. Но с прямыми AB и BS уже есть точки пересечения: M и N.

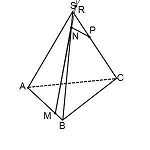
Значит, продлевая MN, ищем точку пересечения ее с прямой AS. Назовем эту точку R.

Точка R лежит на прямой AS, значит, она лежит и в плоскости (ACS), 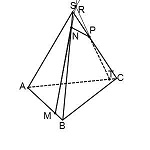которой принадлежит прямая AS.

Поскольку точка P лежит в плоскости (ACS), через R и P можем провести прямую. Получаем след PT.

Точка T лежит в плоскости (ABC), поэтому через нее и точку M можем провести прямую.

Таким образом, получили все то же сечение MNPT.

Рассмотрим еще один пример такого рода.

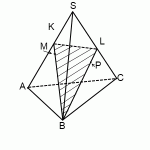
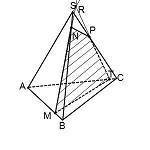
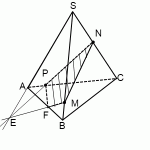
Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.

Через точки M и N, лежащие в одной плоскости (BCS), проводим прямую. Получаем след MN (видимый).

Через точки N и P, лежащие в одной плоскости (ACS), проводим прямую. Получаем след PN (невидимый).

Через точки M и P прямую провести не можем.

1) Прямая MN лежит в плоскости (BCS), где есть еще три прямые: BC, SC и SB. С прямыми SB и SC уже есть точки пересечения: M и N. Поэтому ищем точку пересечения MN с BC. Продолжив эти прямые, получаем точку L.

Точка L принадлежит прямой BC, а значит, она лежит в плоскости (ABC). Поэтому через L и P, которая также лежит в плоскости (ABC) можем провести прямую. Ее след — PF.

F лежит на прямой AB, а значит, и в плоскости (ABS). Поэтому через F и точку M, которая также лежит в плоскости (ABS), проводим прямую. Ее след — FM. Четырехугольник MNPF — искомое сечение.

2) Другой путь — продолжить прямую PN. Она лежит в плоскости (ACS) и пересекается с прямыми AC и CS, лежащими в этой плоскости, в точках P и N.

Значит, ищем точку пересечения PN с третьей прямой этой плоскости — с AS. Продолжаем AS и PN, на пересечении получаем точку E. Поскольку точка E лежит на прямой AS, принадлежащей плоскости (ABS), то через E и точку M, которая также лежит в (ABS), можем провести прямую. Ее след — FM. Точки P и F лежат водной плоскости (ABC), проводим через них прямую и получаем след PF (невидимый).

Источник

Задание 3. Многогранники

4.1. Краткие теоретические сведения

Многогранниками называются тела, ограниченные плоскими n-угольниками, которые называются гранями . Линии пересечения граней называются ребрами , точки пересечения ребер – вершинами. Для всех многогранников справедлива формула Эйлера: сумма граней и вершин за минусом числа ребер есть величина постоянная: Г + В – Р = 2.

Наиболее распространенными в технике многогранниками являются правильные и неправильные, прямые и наклонные призмы и пирамиды. Призмой называется многогранник, в основании которого находится плоский n-угольник, а остальные грани являются в общем случае параллелограммами. Пирамидой называется многогранник, в основании которого находится плоский n-угольник, а боковыми гранями являются треугольники с общей вершиной. На эпюре многогранники задаются проекциями ребер, так называемой сеткой ребер .

Типовой задачей для многогранников является задача о пересечении многогранников плоскостями частного и общего положения. Для построения фигуры сечения многогранника плоскостью используют следующие приемы:

• • определение каждой вершины сечения, как точки пересечения ребер многогранника с секущей плоскостью ( способ ребер );

• построение стороны сечения, как линии пересечения с секущей плоскостью граней многогранника ( способ граней ).

Чаще применяется первый из заданных приемов, второй же целесообразно применять в тех случаях, когда грани многогранника являются проецирующими плоскостями, линии пересечения которых с секущей плоскостью общего положения строятся очень просто.

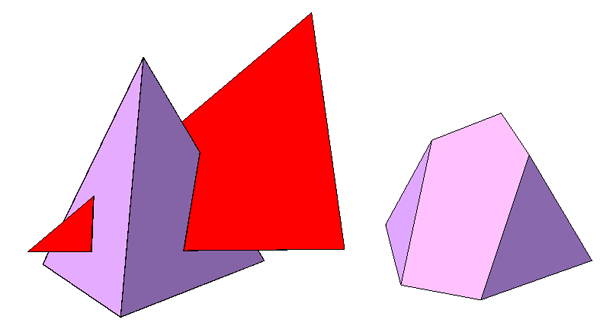
а б
Рисунок 4.1 – Пересечение пирамиды плоскостью (а — задание, б — результат)

В методе ребер несколько раз (по числу пересекаемых ребер) решается задача о пересечении прямой (ребра) с плоскостью (секущей плоскостью). В этом случае находятся точки 1, 2, 3 (рис. 4.1). Найденные точки являются вершинами сечения пирамиды плоскостью.

В методе граней несколько раз решается типовая задача о пересечении двух плоскостей (граней многогранника и секущей плоскости), в которой находят линии 1-2, 2-3, 3-1, являющиеся сторонами многоугольника (в данном примере, треугольника сечения). Если секущая плоскость является плоскостью частного положения, то задача решается упрощенно.

4.2. Способ перемены плоскостей проекций

Сущность способа перемены плоскостей проекций заключается в том, что положение геометрических элементов (точек, прямых, фигур, тел) в пространстве остается неизменным, а система плоскостей проекций заменяется новой, по отношению к которой эти элементы занимают положение, наиболее удобное для решения той или иной задачи.

В ряде случаев для решения задачи бывает достаточно заменить новой плоскостью одну из основных плоскостей проекций – фронтальную или горизонтальную. В других же случаях замена лишь одной плоскости проекций вопроса не разрешает и бывает необходимо последовательно заменить новыми плоскостями обе основные плоскости проекций.

При замене основной плоскости проекций новой плоскостью эта последняя должна располагаться по отношению к остающейся основной плоскости проекций перпендикулярно.

Рассмотрим способ перемены плоскостей проекций на примерах.

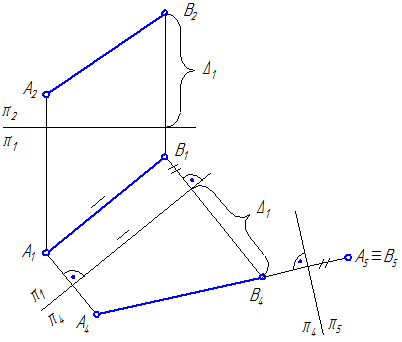
Для того чтобы данная прямая общего положения m=АВ оказалась линией уровня, следует ввести новую плоскость проекций π₄, которая была бы ей параллельна (рис. 4.2 и 4.3).

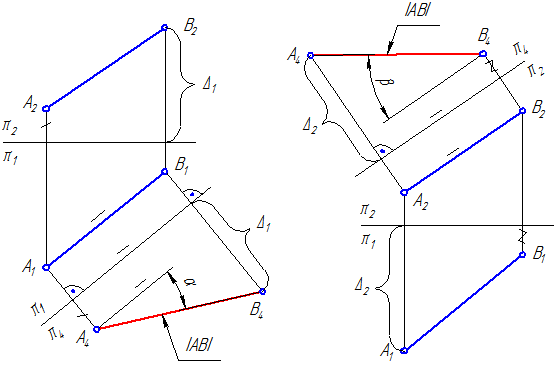
Рисунок 4.2 Рисунок 4.3

На Рисунке 4.2 введена плоскость π₄, параллельная прямой m и перпендикулярная к плоскости π₁; по новым линиям связи от оси π₁/π₄ откладываем расстояния от точек А и В до плоскости π₁ (отмеченное штрихом и D₁). В новой системе плоскостей проекций π₁/π₄ прямая m является линией уровня.

На Рисунке 4.3 плоскость π₄ параллельна прямой m=АВ и перпендикулярна к плоскости π₂. Прямая m в системе π₂/π₄ является линией уровня.

Для того чтобы прямая линия была проецирующей прямой вводится плоскость проекций, перпендикулярная к ней. Для прямой общего положения требуется провести две замены плоскостей проекций. На Рисунке 4.4 прямая m=АВ спроецирована на параллельную ей плоскость π₄. Затем вводится плоскость проекций π₅, перпендикулярная m₄. В системе плоскостей проекций π₅/π₄ прямая m проецируется в точку.

Рисунок 4.4 – Проецирование отрезка прямой в точку

Чтобы определить натуральную величину плоской фигуры общего положения (Рисунок 4.5), требуется сначала ввести такую плоскость проекций π₄, чтобы образовалась система, в которой плоскость α, заданная треугольником АВС будет проецирующей. Данную подзадачу можно решить, введя дополнительную плоскость проекций π₄ перпендикулярно либо горизонтальной проекции горизонтали, либо фронтальной проекции фронтали. Затем вводится дополнительная плоскость π₅, перпендикулярная к плоскости π₄ и параллельная плоскости α .

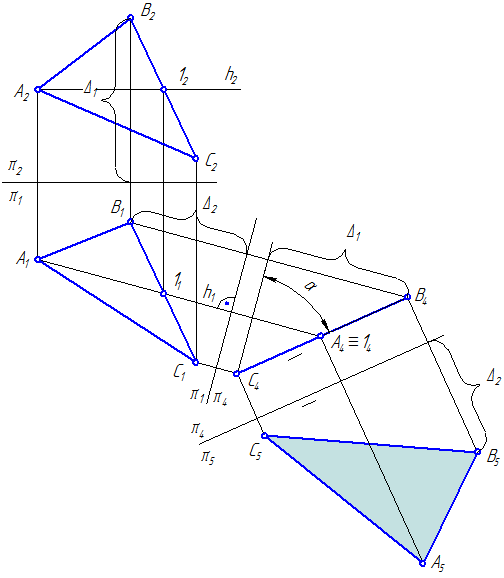
Рисунок 4.5 – Определение натуральной величины треугольника

4.3. Развертывание поверхностей

Разверткой называется плоская фигура, получаемая путем совмещения с плоскостью чертежа поверхности тела.

Построение разверток имеет большое значение в таких областях техники, как котлостроение, судостроение, кровельное и жестяночное дело, продукция которых изготовляется из листового материала.

Точные развертки могут быть построены лишь для линейчатых поверхностей, смежные положения образующих которых параллельны (цилиндрическая поверхность) или пересекаются (коническая поверхность).

Для нелинейчатых поверхностей, образующей которых является кривая линия (например, сферическая поверхность), можно построить развертки лишь приближенные. С этой целью такие поверхности разбиваются на небольшие элементы, и каждая такая часть кривой поверхности заменяется плоскостью. Это означает, что данная кривая поверхность заменяется вписанным в нее многогранником, развертка которого приближенно принимается за развертку кривой поверхности.

Развертка боковой поверхности пирамиды (Рисунок 4.7) состоит из трех треугольников, представляющих в истинном виде боковые грани пирамиды.

Для построения развертки необходимо предварительно определить истинные длины боковых ребер пирамиды. Повернув эти ребра вокруг высоты пирамиды до положения параллельного плоскости ?₂, на фронтальной плоскости проекций получим их истинные длины в виде отрезков S₂ A ₂, S₂ B ₂, S₂ C ₂ (Рисунок 4.6).

Построив по трем сторонам S₂ A ₂, S₂ B ₂ и A₁B₁ грань пирамиды ASB (Рисунок 4.7), пристраиваем к ней смежную грань – треугольник BSC, а к последнему – грань CSA. Полученная фигура представит собою развертку боковой поверхности данной пирамиды.

Для получения полной развертки к одной из сторон основания пристраиваем основание пирамиды – треугольник АВС.

Для построения на развертке линии, по которой поверхность пирамиды пересечется плоскостью α (Рисунок 4.7), следует нанести на ребра SA, SB и SC, соответственно, точки 1, 2 и 3, в которых эта плоскость пересекает ребра, определив истинные длины отрезков S1, S2 и S3.

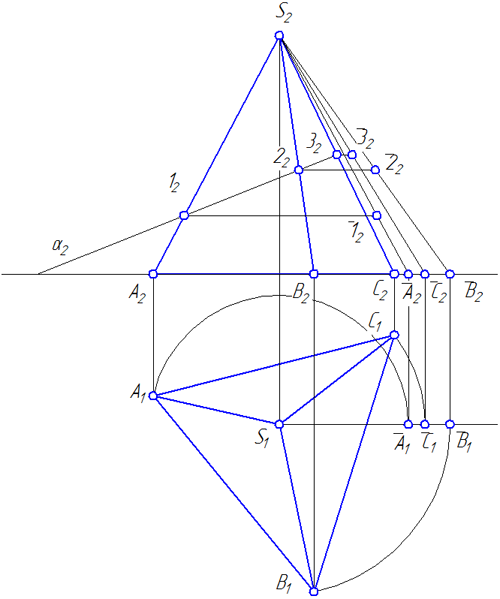
Рисунок 4.6 – Определение истинных длин ребер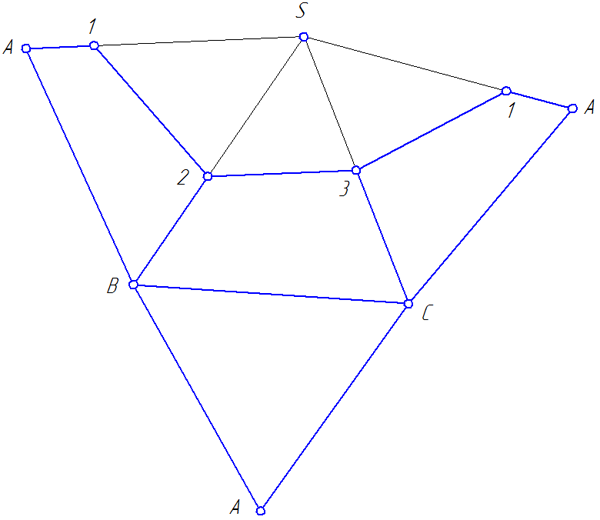

Рисунок 4.7 – Построение развертки

4.4. Задание 3. Построение натурального вида сечения пирамиды плоскостью

4.4.1. Условие задания

Задание следует выполнять в соответствии с алгоритмом:

1. 1. По координатам вершин (Таблицы 3.1- 3.3) построить: две проекции пирамиды 1234S;

1. 1. Выполнить две проекции сечения пирамиды плоскостью общего положения АВС (Таблица 3.4);

1. 1. Найти натуральный вид сечения способом перемены плоскостей проекций;

1. Выполнить развертку верхней отсеченной части пирамиды.

4.4.2. Рекомендации по выполнению задания № 2

Порядок выполнения задачи следующий:

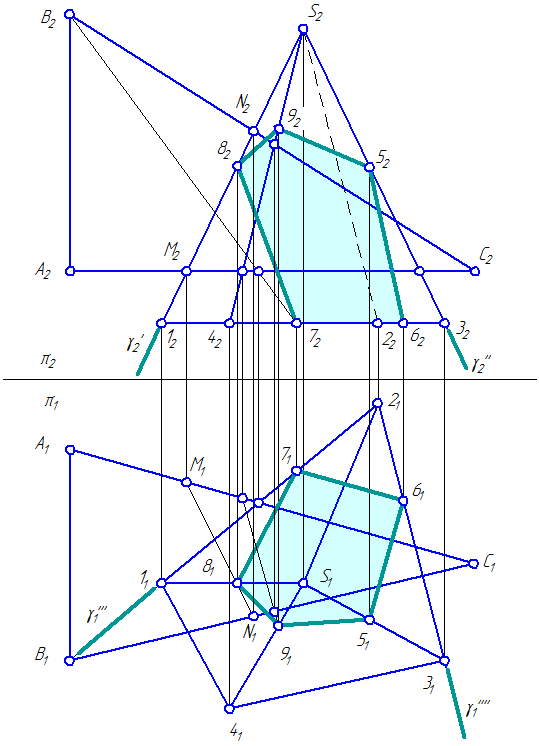
1. Построить горизонтальные и фронтальные проекции пирамиды и 1234S и плоскости ∆АBC (Рисунок 4.8);
2. Способом ребер или способом граней построить проекции сечения пирамиды 1234S плоскостью ∆АBC.

Способ ребер заключается в том, что ребро пирамиды (например, 1S) заключается во фронтально-проецирующую плоскость γ: γπ₂≡1₂S₂. Затем выполняется построение точки 8 пересечения ребра 1S с плоскостью γ:

Аналогично выполняется построение остальных точек искомого сечения.

Способом граней строятся линии пересечения с помощью плоскостей-посредников;

Рисунок 4.8 – Построение сечения

1. Способом перемены плоскостей проекций найти натуральный вид сечения 56789.

Сущность способа перемены плоскостей проекций состоит в том, что положение геометрического образа (прямой, плоскости, поверхности) в пространстве остается неизменным, а система плоскостей проекций π₁/π₂ дополняется плоскостями, образующими с π₁ или π₂, либо между собой системы двух взаимно перпендикулярных плоскостей проекций. Расположение новой плоскости проекций по отношению к геометрическим образам выбирается в зависимости от условия задачи.

В данной задаче необходимо дважды ввести новые плоскости проекций: в системе плоскостей π₁/π₄ сечение 56789 станет проецирующей плоскостью, а в системе плоскостей проекций π₄/π₅ – плоскостью уровня;

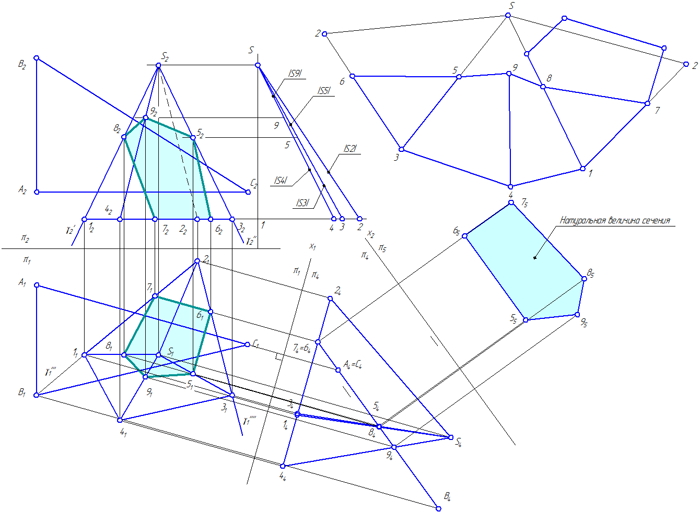
Рисунок 4.9 – Пересечение пирамиды плоскостью общего положения

1. Выполнить развертку нижней отсеченной части пирамиды.

Видеопример выполнения задания №3

4.5. Варианты задания 3

Таблица 3.1– Значения координат точек (для вариантов с 1 по 10)

S	1	2	3	4
X	50	90	30	10	70
Y	50	50	5	70	80
Z	90	10	10	10	10

Таблица 3.2– Значения координат точек (для вариантов с 11 по 20)

S	1	2	3	4
X	50	90	30	10	70
Y	50	50	5	70	80
Z	90	0	0	0	0

Таблица 3.3– Значения координат точек (для вариантов с 21 по 30)

S	1	2	3	4
X	50	100	25	5	80
Y	50	50	5	70	80
Z	100	10	10	10	10

Таблица 3.4– Значения координат точек

Вариант	Координаты (x, y, z) точек			Вариант	Координаты (x, y, z) точек
	А	В	С		А	В	С
1	100;15;30	35; 85; 90	10; 45; 30	16	90; 0; 0	100; 50; 70	5; 55; 40
2	65; 10; 0	100; 50; 80	20; 80; 80	17	95; 35; 40	50; 35; 0	5; 65; 50
3	100; 25;40	15; 90; 90	50; 15; 0	18	50; 50; 45	0; 55; 0	100; 20; 5
4	30; 80; 90	20; 25; 0	100; 25; 40	19	30; 90; 60	90; 30; 20	0; 35; 0
5	100; 15; 20	100; 60; 90	10; 45; 20	20	95; 15; 0	5; 60; 20	70; 85; 80
6	90; 0; 0	100; 50; 80	5; 55; 40	21	100;15;30	35; 85; 90	10; 45; 30
7	95; 35; 50	50; 35; 0	5; 65; 50	22	65; 10; 0	100; 50; 80	20; 80; 80
8	50; 50; 55	0; 55; 5	100; 20; 5	23	100; 25;40	15; 90; 90	50; 15; 0
9	30; 90; 70	90; 30; 30	0; 35; 0	24	30; 80; 90	20; 25; 0	100; 25; 40
10	95; 15; 10	5; 60; 30	70; 85; 80	25	100; 15; 20	100; 60; 90	10; 45; 20
11	100;15;20	35; 85; 80	10; 45; 30	26	90; 0; 0	100; 50; 80	5; 55; 40
12	65; 10; 0	100; 50; 70	20; 80; 80	27	95; 35; 50	50; 35; 0	5; 65; 50
13	100; 25;30	15; 90; 80	50; 15; 0	28	50; 50; 55	0; 55; 5	100; 20; 5
14	30; 80; 80	20; 25; 0	100; 25; 40	29	30; 90; 70	90; 30; 30	0; 35; 0
15	100; 15; 10	100; 60; 80	10; 45; 20	30	95; 15; 10	5; 60; 30	70; 85; 80

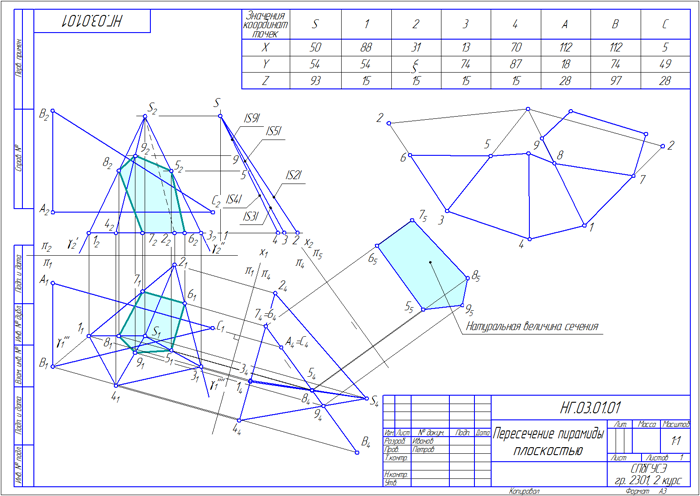
Рисунок 4.10 – Пример оформления задания 3

Источник