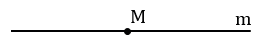Способы построения перпендикулярных прямых

Построение перпендикулярных прямых

Примеры:

1. Даны прямая и точка на ней. Построить прямую проходящую через данную точку и перпендикулярную к данной прямой.

Дано: прямая m, Mm.

Построить: МPm.

Решение:

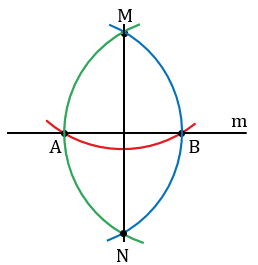
Произвольно строим с помощью линейки прямую m и отмечаем на ней точку М.

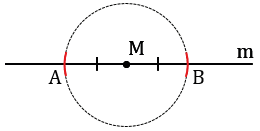
На лучах прямой m, исходящих из точки М, с помощью циркуля откладываем равные отрезки МА и МВ (МА = МВ). Для этого строим окружность с центром в точке М, при этом всю окружность строить не обязательно, достаточно сделать пометки по разные стороны от точки М (смотри выделенное красным).

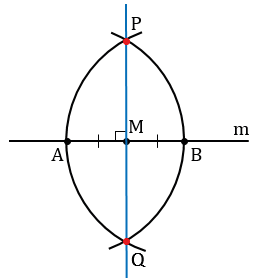
Затем строим две окружности с центрами в точках А и В радиуса АВ (полностью окружности строить необязательно, смотри выделенное фиолетовым и красным цветом).

Данные окружности пересекаются в двух точках, обозначим их Р и Q. Проведем с помощью линейки через точку М и одну из точек Р или Q прямую, например, МР.

Докажем, что прямая МР — искомая прямая, т.е. что МPm.

Рассмотрим треугольник АРВ.

АР = ВР, т.к. по построению это радиусы одинаковых окружностей, следовательно, АРВ — равнобедренный. По построению МА = МВ, т.е. МР — медиана равнобедренного треугольника, тогда по свойству равнобедренного треугольника МР и высота, т.е. МPm. Что и требовалось доказать.

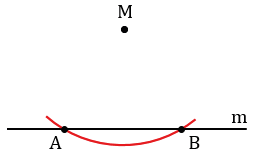
2. Даны прямая и точка не лежащая на этой прямой. Построить прямую проходящую через данную точку и перпендикулярную к данной прямой.

Дано: прямая m, Mm.

Построить: МNm.

Решение:

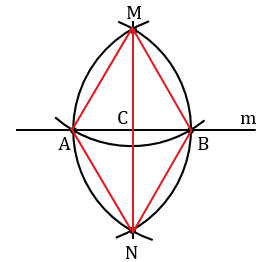
Произвольно строим с помощью линейки прямую m и отмечаем точку М, не лежащую на прямой m.

Далее строим окружность с центром в данной точке М, пересекающую прямую m в двух точках, которые обозначим буквами А и В (всю окружность строить необязательно, смотри выделенное красным цветом).

Затем построим две окружности с центрами в точках А и В, проходящие через точку М (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Эти окружности пересекутся в точке М и еще в одной точке, которую обозначим буквой N. Проведем прямую МN.

Докажем что, прямая МN — искомая, т.е. МNm.

В АМN и ВМN: АМ = АN = ВМ = ВN — радиусы, МN — общая, следовательно, АМN =ВМN (по трем сторонам), значит, углы ВМС и АМС равны (С точка пересечения прямых m и МN). Отсюда следует, что отрезок МС — биссектриса равнобедренного треугольника АМВ (АМ = ВМ — радиусы) с основанием АВ, тогда по свойству равнобедренного треугольника АМ — высота, значит, МNАВ, т.е. МNm.

Поделись с друзьями в социальных сетях:

Источник

Способы построения перпендикулярных прямых

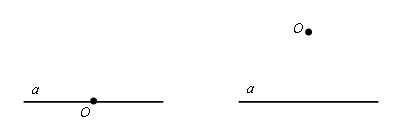
Через точку O провести прямую, перпендикулярную данной прямой a.

Возможно два варианта:

1. точка O лежит на прямой a;
2. точка О не лежит на прямой a.

Рассмотрим поочередно оба варианта.

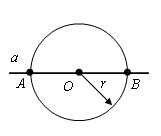
Шаг 1. Проводим окружность с произвольным радиусом r с центром в точке O. Окружность пересекает прямую в точках A и B.

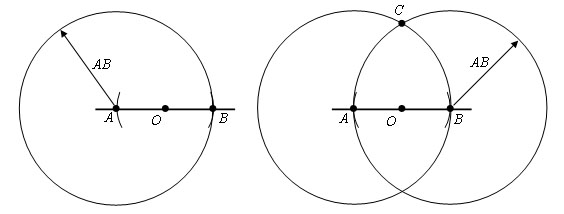
Шаг 2. Из точек A и B проводим окружности с радиусом AB. Пусть тоска С – точка пересечения этих окружностей.

Обращаю ваше внимание на то что точки А и В мы получили на первом шаге, при построении окружности с произвольным радиусом.

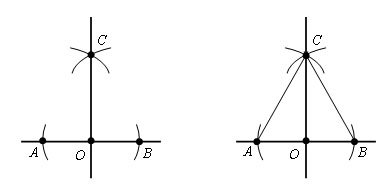
Шаг 3. Искомая прямая проходит через точки С и О.

Проведем отрезки AC и CB. Δ ACO = Δ BCO по третьему признаку равенства треугольников (AO = OB, AC = CB, по построению, CO – общая). ∠ COA = ∠ COB = 90 °. Прямая CO ⊥ AB.

Как было уже сказано выше все четыре угла образованных при пересечении двух прямых перпендикулярны если хотя бы один из них перпендикулярен, т.е. является прямым и равен 90 градусов.

Второй вариант такой же простой только имеет немного другой принцип поиска наших начальных точек А и В.

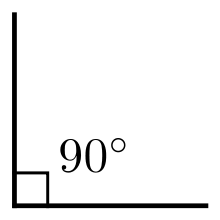
Шаг 1. Из точки O проводим окружность некоторым радиусом r, таким чтобы окружность пересекала прямую a. Пусть A и B – точки пересечения окружности с прямой a.

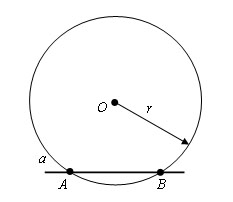
Шаг 2. Проведем окружности тем же радиусом r с центрами в точках A и B. Пусть точка O₁ – точка пресечения этих окружностей, лежащая в полуплоскости, отличной от той, в которой лежит точка O.

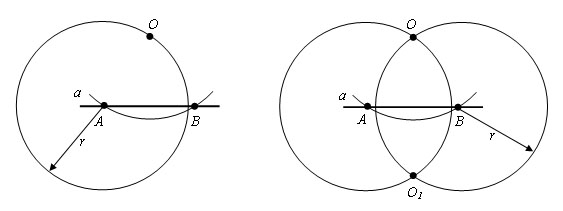
Шаг 3. Проведем через точки O и O₁ прямую. Это и будет искомая прямая.

Пусть прямые OO₁ и AB пересекаются в точке С. Δ AOB = Δ BO₁A по третьему признаку равенства треугольников (AO = OB = AO₁ = O₁B, по построению, AB – общая). Отсюда следует, что ∠ OAС = ∠ O₁AC. Δ OAC = Δ O₁AC по первому признаку равенства треугольников (AO = AO₁, по построению, ∠ OAС = ∠ O₁AC, AС – общая). Следовательно ∠ OСA = ∠ O₁CA, а так как эти углы смежные, то они прямые. Поэтому OC – перпендикуляр, опущенный из точки O на прямую a.

Т. е. с помощью циркуля и линейки мы можем стоить перпендикулярные прямые, независимо от того точка через какую должен проходить перпендикуляр находиться на отрезке или за его пределами. Оба варианта имеют три шага, единственная сложность в том что бы правильно найти начальные точки А и В.

Источник

Урок 44 Бесплатно Перпендикулярные прямые

До этого на уроках математики мы работали с числами, буквами, выражениями.

Иногда не только писали, но и рисовали схемы, координатные прямые и рисунки, чтобы лучше разбираться в изучаемом вопросе.

Сегодня мы будем изучать геометрические понятия, а именно, что является прямой, а что нет, какие прямые называются перпендикулярными.

Также узнаем, как строить перпендикулярные прямые разными способами.

Основные определения

В геометрии есть два понятия, которые не имеют определения, их мы принимаем как аксиомы.

Это понятия точки и прямой.

Все остальные определения будут так или иначе выражаться через эти два понятия.

Определение: луч или полупрямая — это часть прямой, состоящая из данной точки и всех точек, лежащих по одну сторону от нее.

Заметим, что любая точка, лежащая на прямой, разделяет эту прямую на два луча.

Разделяющую точку также называют началом луча.

Определение: отрезок — часть прямой, ограниченная двумя точками.

И еще немного формализма.

Определение: угол — геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.

Эти лучи называют сторонами угла, а их общее начало вершиной угла.

Есть величины для измерения длины: метр, сантиметр, километр и прочие производные метра.

Для измерения угла используются другие величины: градусы, минуты, секунды, радианы.

Одним из наиболее простых приборов для измерения углов является транспортир. Достаточно приложить его прямую часть к одной стороне угла и посмотреть, какое деление совпадет со второй стороной угла.

Главное, быть внимательным и смотреть, с какой стороны находится внутренняя часть угла.

Допустим, имеется такая конфигурация:

Углы обычно обозначаются тремя буквами, где буква посередине обозначает вершину угла.

Величина угла AOB будет равняться 45-ти градусам, можно записать как \(\mathbf<45^\circ>\).

Если необходимо измерить угол BOC, то нужно из 180-ти градусов вычесть 45 градусов, так как метки на транспортире соответствуют величинам углов, если считать от нуля, а в данном случае луч ОС лежит на отметке 180.

Также часто перед буквенным обозначением угла ставят следующий знак: \(\mathbf<\angle>\), получаются такие записи: \(\mathbf<\angle AOB>\), \(\mathbf<\angle BOC>\).

Иногда, когда нет неоднозначности, угол могут обозначать и одной буквой, например \(\mathbf<\angle A>\)

Определение: прямой угол — угол в \(\mathbf<90^\circ>\).

На транспортире данная отметка находится посередине.

Если обычный угол часто обозначают маленькой дугой, то прямые углы принято обозначать таким квадратиком.

Прямой угол один из самых распространенных в мире: с большой вероятностью вы сейчас сидите в комнате с такиими углами, у вашего стола прямые углы, а также у окна и так далее.

Теперь мы подготовили все определения, чтобы определить термин из заголовка урока.

Определение: две прямые, образующие при пересечении прямые углы, называют перпендикулярными.

Прямые часто обозначают одной строчной латинской буквой. В данном случае прямые a и b перпендикулярные по определению, потому что образуют прямые углы.

Если бы они пересекались под другим углом или не пересекались бы, то они не были бы перпендикулярными. В данном случае прямые a и b не являются перпендикулярными.

Пройти тест и получить оценку можно после входа или регистрации

Построение прямого угла и перпендикулярных прямых

Перечислим основные способы в порядке возрастания сложности.

Самый простой способ взять предмет с прямым углом- чертежный треугольник, линейку, банковскую или проездную карту (придется только дорисовать скошенный угол от руки), и обвести его.

Правда, мы не можем гарантированно полагаться на перечисленные кроме треугольника предметы, так как они не предназначены для черчения, и угол может быть не совсем прямым.

Лучи, являющиеся сторонами угла, будут перпендикулярны, а значит, будут частями перпендикулярных прямых.

Также можно построить любой угол, в том числе прямой, с помощью транспортира.

1) Вершину угла мы ставим в центре прямой части транспортира.

2) Одни сторону проводим по прямой части транспортира в сторону нуля.

3) Ставим метку напротив риски с соответствующей величиной угла.

4) Соединяем вершину угла с меткой.

Аналогичным образом строится прямой угол.

В таком случае его стороны опять же будут перпендикулярными лучами, следовательно, частями перпендикулярных прямых.

Прежде чем перейти к более сложному и интересному способу, надо упомянуть, что клетки в тетради начерчены перпендикулярными прямыми, поэтому можно от руки обвести одну вертикальную линию и одну горизонтальную.

Скорее всего линии получатся не совсем прямыми, но если это нужно для какой-то схемы в черновике, то почему бы и нет.

Хотя конечно же во всех работах лучше использовать приборы и линейку чтобы рисунок был максимально красивым.

Интересно, что перпендикулярные прямые можно построить с помощью циркуля и линейки без разметки (ну и карандаша/ручки, конечно же).

Подробнее, почему алгоритм является корректным, вы узнаете в курсе геометрии за 7-й класс, но пока что посмотрим на сам алгоритм.

1) Чертим прямую и отмечаем на ней точку (назовем ее О).

2) Ставим в эту точку циркуль и с помощью него делаем две пометки, получаем две точки, равноудаленные от первой точки (назовем из А и В).

3) Проводим из каждой из точек А и В окружности одинакового радиуса, или лучше только нужные их части, так чтобы получить хотя бы одно пересечение (назовем его точной С).

4) Соединяем точку С с исходной точкой О, готово, мы получили перпендикулярную прямую, причем проходящую через точку, которую мы сами выбрали.

В этом алгоритме важна аккуратность: если точки А и В будут на разном расстоянии от центра или окружности из точек А и В будут разного радиуса, прямая может получится не перпендикулярной.

Пройти тест и получить оценку можно после входа или регистрации

Источник