Чертежик

Метки

Построение овала

Рассмотрим построение овала двумя методами: окружности и параллелограмма.

Воспользуемся методом окружности.

1.) Начинаем чертить с построения осей.

2.) Чертим окружность

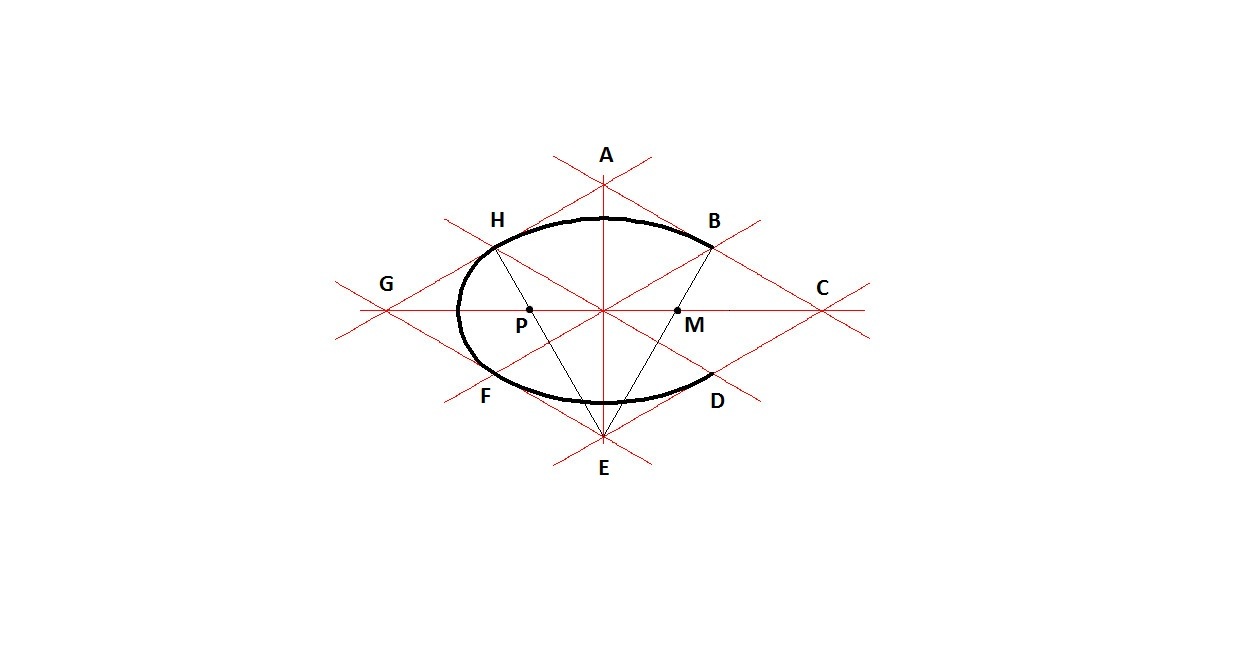
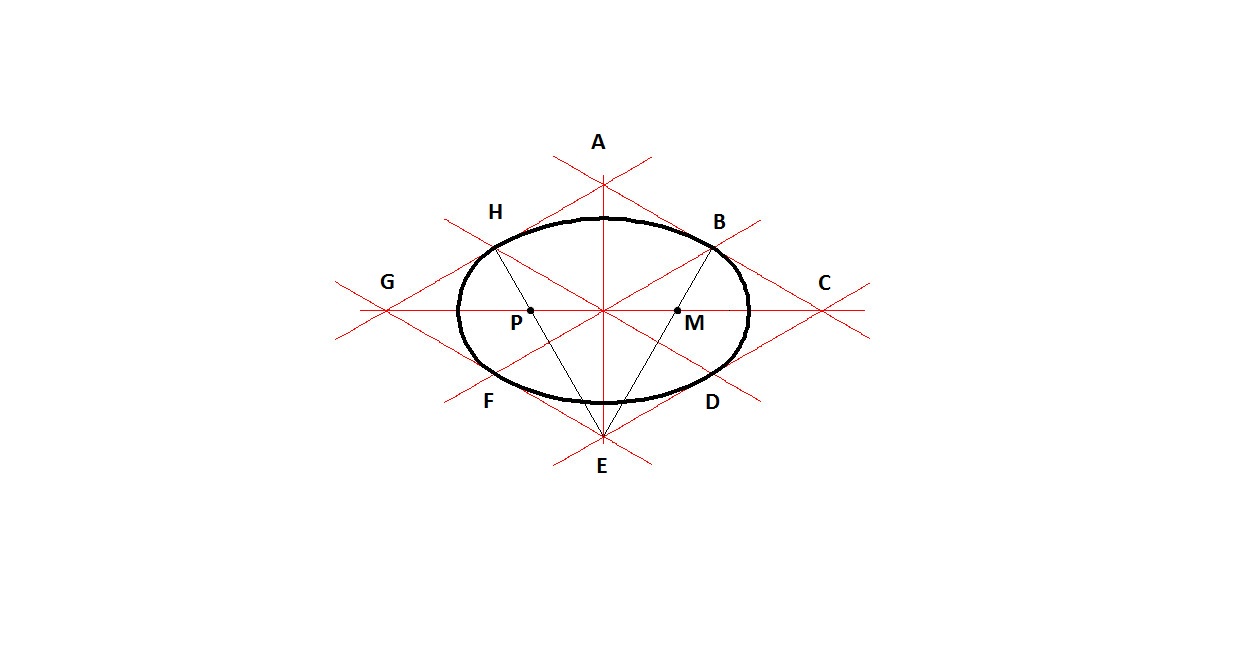
3.) Чертим дуги ЕА и BD радиусом ЕС

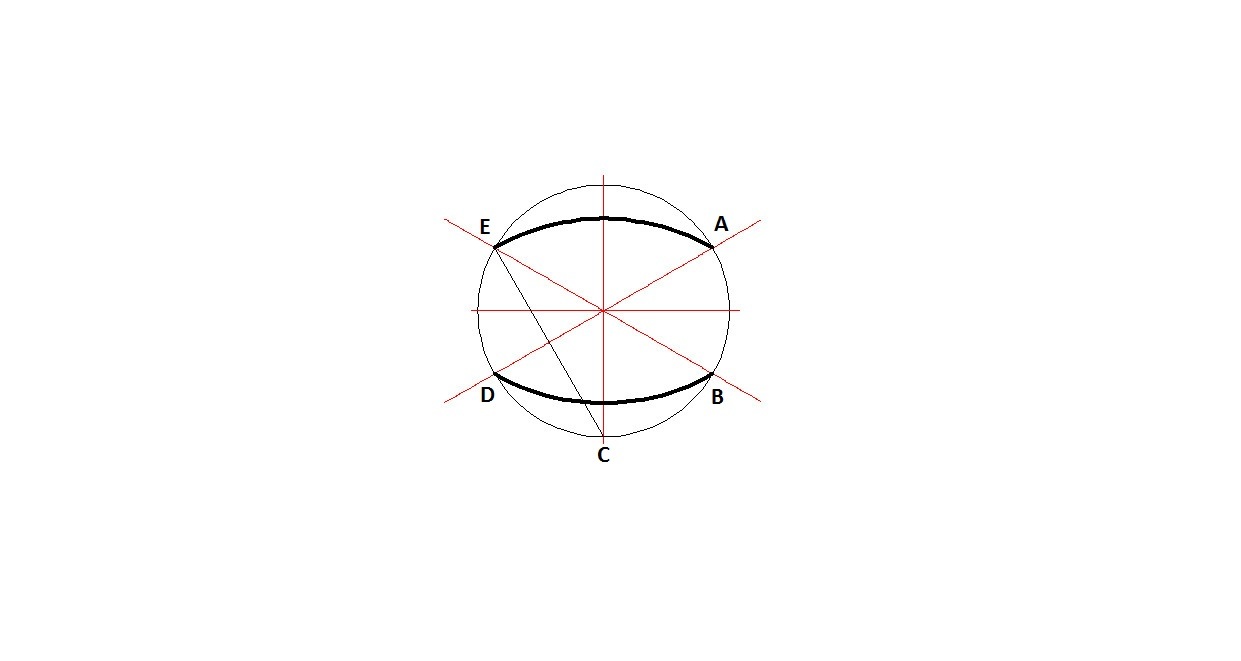
4.) Чертим дуги ED и AB радиусом FB

Применим метод параллелограмма.

1.) Начинаем с построения осевых линий

2.) Чертим линии параллельные осевым линиям. Где d — диаметр окружности.

3.) Строим дуги HB и DF радиусом HE4.) Продолжаем с черчения дуги BD радиуса MB и дуги FH радиусом PH

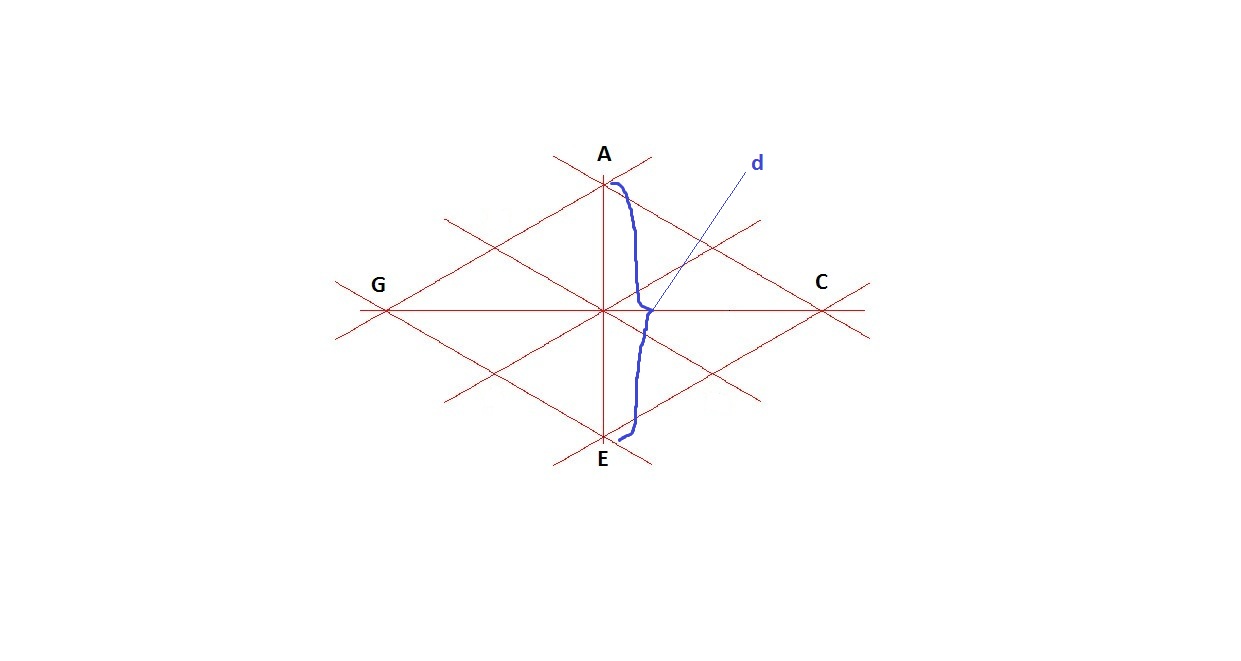
Применение построения овала на чертежах вы можете посмотреть здесь

Источник

Глава 3. Некоторые геометрические построения

§ 21. Овалы

Плавные выпуклые кривые, очерченные дугами окружностей разных радиусов, называют овалами . Овалы состоят из двух опорных окружностей с внутренними сопряжениями между ними.

Различают овалы трехцентровые и многоцентровые. При вычерчивании многих деталей, например кулачков, фланцев, крышек и других, контуры их очерчивают овалами.

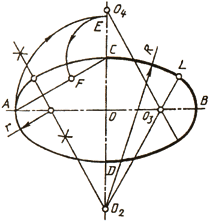
Рассмотрим пример построения овала по заданным осям. Пусть для четырехцентрового овала, очерченного двумя опорными дугами радиуса R и двумя сопрягающими дугами радиуса r, заданы большая ось АВ и малая ось CD. Величину радиусов R и r надо определить путем построений (рис. 36). Соединим концы большой и малой оси отрезком АС, на котором отложим разность СЕ большой и малой полуосей овала. Проведем перпендикуляр к середине отрезка AF, который пересечет большую и малую оси овала в точках О и О₂. Эти точки будут центрами сопрягающихся дуг овала, а точка сопряжения будет лежать на самом перпендикуляре.

© Красноярский государственный аграрный университет
© Управление информационных технологий
© Кафедра Технологии машиностроения

Источник

Овал. Определение овала и способы его построения

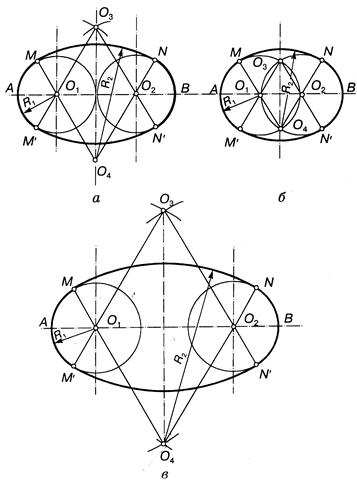
Овал — это замкнутая коробовая кривая, имеющая две оси симметрии и состоящая из двух опорных окружностей одинакового диаметра, внутренне сопряженных дугами (рис. 13.45). Овал характеризуется тремя параметрами: длина, ширина и радиус овала. Иногда задают только длину и ширину овала, не определяя его радиусов, тогда задача построения овала имеет большое множество решений (см. рис. 13.45, а. г).

Применяют также способы построения овалов на основе двух одинаковых опорных кругов, которые соприкасаются (рис. 13.46, а), пересекаются (рис. 13.46, б) или не пересекаются (рис. 13.46, в). При этом фактически задают два параметра: длину овала и один из его радиусов. Эта задача имеет множество решений. Очевидно, что R > ОА не имеет верхней границы. В частности R = О₁О₂ (см. рис. 13.46.а, и рис. 13.46.в), а центры О₃ и О₄ определяют, как точки пересечения базовых кругов (см. рис. 13.46,б). Согласно общей теорией точки, сопряжения определяются на прямой, соединяющей центры дуг соприкасающихся окружностей.

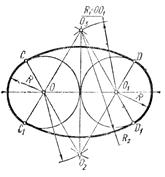
Построение овала с соприкасаю­щимися опорными окружностями (задача имеет множество решений) (рис. 3.44). Из центров опорных окружностей О и 0₁ радиусом, равным, например, расстоянию между их центрами, проводят дуги окруж­ностей до пересечения в точках О₂и О₃.

Если из точек О₂и О₃ провести прямые через центры О и O₁, то в пересечении с опорными окружнос­тями получим точки сопряжения С, C₁, D и D₁. Из точек О₂и О₃ как из центров радиусом R₂ проводят дуги сопряжения.

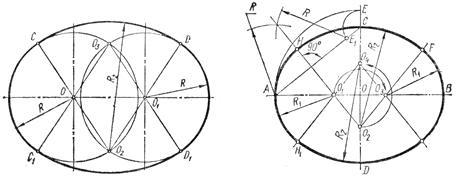
Построение овала с пересека­ющимися опорными окружностями (задача также имеет множество решений) (рис. 3.45). Из точек пе­ресечения опорных окружностей С₂ и О₃ проводят прямые, например, через центры О и O₁ до пересечения с опорными окружностями в точках сопряжения С, С₁ D и D₁, а ра­диусами R₂, равными диаметру опорной окружности,— дуги со­пряжения.

Рисунок 3.45 Рисунок 3.46

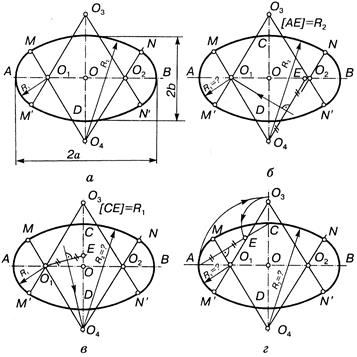
Построение овала по двум задан­ным осям АВ и CD (рис. 3.46). Ниже приведен один из множества вариантов решения. На верти­кальной оси откладываются отре­зок ОЕ, равный половине большой оси АВ. Из точки С как из центра проводят дугу радиусом СЕ до пе­ресечения с отрезком АС в точке Е₁. К середине отрезка АЕ₁ восстанавливают перпендикуляр и отмечают точки его пересечения с осями ова­ла O₁ и 0₂. Строят точки O₃ и 0₄, симметричные точкам O₁ и 0₂ от­носительно осей CD и АВ. Точки O₁ и 0₃ будут центрами опорных ок­ружностей радиуса R₁, равного от­резку О₁А, а точки O₂ и 0₄ — цент­рами дуг сопряжения радиуса R₂, равного отрезку О₂С. Прямые, со­единяющие центры O₁ и 0₃ с O₂ и 0₄ в пересечении с овалом опреде­лят точки сопряжения.

В AutoCAD построение овала производится с помощью двух опорных окружностей одинакового радиуса, которые:

1. имеют точку соприкосновения;

3. не пересекаются.

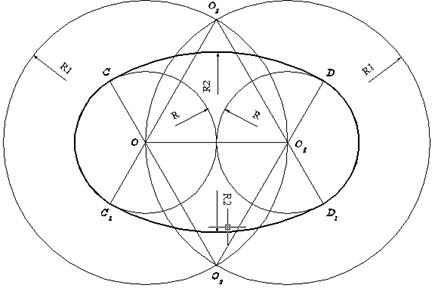
Рассмотрим первый случай. Строят отрезок OO₁=2R, параллельный оси Х, на его концах (точки О и О₁) размещают центры двух опорных окружностей радиуса R и центры двух вспомогательных окружностей радиуса R₁=2R. Из точек пересечения вспомогательных окружностей О₂ и О₃ строят дуги CD и C₁D₁ соответственно. Удаляют вспомогательные окружности, затем относительно дуг CD и C₁D₁ обрезают внутренние части опорных окружностей. На рисунке ъъъ полученный овал выделен толстой линией.

Рисунок Построение овала с соприкасающимися опорными окружностями одинакового радиуса

Источник

План-конспект урока по черчению на тему «Понятие о лекальных и циркулярных кривых, построение овала и эллипса»

План урока по черчению

Тема: Построение овала, эллипса.

Образовательная: сформировать знания учащихся по новой теме, научиться строить овал и эллипс;

Развивающая: развивать аккуратность, эстетический вкус, развивать познавательный интерес и интеллект у учащихся, а так же навыки черчения;

Воспитательная: воспитывать бережное отношение к предметам и приспособлениям, воспитывать чувство взаимопомощи, дисциплинированность, воспитывать усидчивость, прилежность и самостоятельность.

Тип урока: комбинированный

Программное дидактическое оснащение : учебник по черчению, чертежные инструменты, доска.

1. Организационный момент (2-3 мин);

2. Повторение пройденного материала (3 мин);

3. Изучение нового материала (10 мин);

4. Практическая работа (20 мин);

5. Подведение итогов. Рефлексия (3 мин);

6. Домашнее задание (2 мин).

Приветствие. Проверка отсутствующих, наличия учебных принадлежностей.

Повторение пройденного материала.

Прежде чем мы начнем изучать новую тему, давайте повторим тему прошлых уроков. Ответьте на следующие вопросы:

1.)Что такое сопряжение? (Сопряжение — плавный переход одной линии в другую)

2)Что такое касательная к окружности? (Прямая называется касательной к окружности, если она имеет только одну общую точку с этой окружностью).

Изучение нового материала.

Некоторые детали машин, инструменты для обработки металлов имеют контуры, ограниченные замкнутыми кривыми линиями, состоящими из взаимносопрягающихся дуг окружностей различных диаметров.

Коробовыми кривыми называются кривые, образованные сопряжением дуг окружностей. К таким кривым относятся овалы, овоиды, завитки.

Овал- замкнутая коробовая кривая, имеющая две оси симметрии.

Построить овал можно двумя способами, в зависимости от изначально заданных параметров.

1 способ: когда задается ширина и высота овала.

2 способ: когда задается только ширина овала.

Рассмотрим 1 способ построения овала

Построение овала по двум заданным осям симметрии (большей и меньшей) выполняется в следующей последовательности:

1. Проводим две оси симетрии, пересекающиеся под прямым углом.

2. На вертикальной оси отложим заданный нам размер ширины овала СD (по половине размера вверх и вниз из точки О). На горизонтальной оси таким же образом отложим длину овала АВ.

3. Соединяем прямой линией точки С и В.

4. Из центра О соединяем горизонтальную и вертикальную ось радиусом ОВ (намечаем точку е)

5. Из точки С проводим дугу радиусом Се до пересечения с наклонной прямой СВ (намечаем точку f).

6. Участок между точками f и B наклонной прямой делим на две равные части. Для этого из точки f проводим дугу радиусом fВ, затем из точки В проводим дугу того же радиуса, до пересечения с дугой, построенной ранее.

7. Соединяем точки пересечения дуг. Эта линия будет являться перпендикуляром к отрезку fВ и будет делить его пополам. Отмечаем точки пересечения построенной линии с горизонтальной и вертикальной осями симетрии (l и k).

8. Строим точку m симметричную точке l.

9. Строим точку n симметричную точке k.

10. Из точки k проводим прямую через точку m. Из точки n проводим прямые мерез точки m и l.

11. Радиусом равным расстоянию kC из точки k проводим дугу, соединяющую наклонные линии, исходящие из точки k. Тем же радиусом из точки n, как из центра, проводим дугу соединяющую наклонные линии исходящие из точки n.

12. Из точек m и l, как из центров, проводим дуги радиусом mA и замыкаем ими ранее проведенные дуги.

На этом построение овала можно считать за к онченым.

Овоид — замкнутая коробовая кривая,имеющая только одну ось симметрии.

Завиток — плоская спиральная кривая, вычерчиваемая циркулем путем сопряжения дуг окружностей.

Построение завитков выполняют при вычерчивании таких деталей, как пружины и спиральные направляющие.

Построение завитков выполняется из двух, трех и более центров и зависит от формы и размеров “глазка”, который может быть окружностью, правильным треугольником, шестиугольником и т.п.

При выполнении чертежей часто приходится прибегать к вычерчиванию кривых, состоящих из ряда сопряженных частей, которые невозможно провести циркулем. Такие кривые строят обычно по ряду принадлежащих им точек, которые затем соединяют плавной линией сначала от руки карандашом, а затем обводят при помощи лекал.

Рассматриваемые лекальные кривые располагаются в одной плоскости и называются поэтому плоскими.

Лекальные кривые широко применяются в машиностроении для очертания различных технических деталей, например: кронштейнов, ребер жесткости, кулачков, зубчатых колес, фасонного инструмента и т.п.

К лекальным кривым относят эллипс, параболу, гиперболу, циклоиду, эпициклоиду, эвольвенту, синусоиду, спираль Архимеда и др.

Эллипс — замкнутая плоская кривая, сумма расстояний каждой точки которой до двух данных точек(фокусов), лежащих на большой оси, есть величина постоянная и равная длине большой оси.

Широко применяемый в технике способ построения эллипса по большой(АВ) и малой(СD) осям.

Проводят две перпендикулярные осевые линии. Затем от центра О откладывают вверх и вниз по вертикальной оси отрезки, равные длине малой полуоси, а влево и вправо по горизонтальной оси-отрезки, равные длине большой полуоси.

Из центра О радиусами ОА и ОС проводят две концентрические окружности и ряд лучей-диаметров. Из точек пересечения лучей с окружностями проводят линии, параллельные осям эллипса, до взаимного пересечения в точках, принадлежащих эллипсу. Полученные точки соединяют от руки и обводят по лекалу.

Построение эллипса вписанного в ромб

Вначале строят ромб со стороной, равной диаметру изображаемой окружности. Для этого через точку О проводят изометрические оси x и y .

На них от точки О откладывают отрезки, равные радиусу изображаемой окружности. Через точки а, b , с, d проводят прямые параллельные осям; получают ромб.

Большая ось овала располагается на большой диагонали ромба.

После этого вписывают в ромб овал. Для этого из вершин тупых углов (точек А и В) описывают дуги.

Их радиус R равен расстоянию от вершины тупого угла (точек А и В) до точек а, b или с,d соответственно.

Через точки B и a , B и b проводят прямые. В пересечении прямых Ba и В b с большей диагональю ромба находятся точки C и D . Эти точки будут центрами малых дуг. Их радиус R , равен С a (или Db ).

Дугами этого радиуса плавно соединяют большие дуги овала.

Для решения некоторых проблем не всегда достаточно глубокого анализа. Иногда умную мысль легче выловить в бушующем море идей, нежели из ровной поверхности размеренной задумчивости. В этом случае оправдано применение техники мозгового штурма, цель которой – быстро найти верное решение.

Упражнение 1. Циркульные кривые.

Работаем в паре с соседом по парте, задание: найти другие способы построения овалов.

Упражнение 2. Лекальные кривые.

Цель задания. Научиться чертить лекальную кривую – эллипс (со сторонами 60мм;30мм)

Подведение итогов. Рефлексия.

Учесть правильность и качество выполненной работы.

д/з: Откройте дневники и запишите домашнее задание: §1.11+ построение в тетради (Выполнить чертеж предмета, форма которого образована на основе циркульных и лекальных кривых (машиностроительной детали, плоской игрушки, ювелирного изделия и т.п.).)

Источник