Способы построения моделей
В зависимости от характера и объема априорной информации выделяют два способа построения моделей объектов и систем управления:
Аналитический способ применяется для построения моделей объектов хорошо изученной природы. В этом случае имеется вся необходимая информация, но она представлена в иной форме. Реализуемые при этом модели представляются в виде схем с сосредоточенными параметрами (компонентами). На таких моделях базируются, например, теоретическая механика и теоретическая электротехника.
Методы теории управления абстрагируются от конкретной природы объектов и оперируют более абстрактными – математическими (символьными) моделями.
Аналитический способ моделирования состоит из двух основных этапов:
− построения схемы объекта;
− построение математического описания схемы в требуемой форме.
При этом принципиальные проблемы моделирования решаются на первом (неформальном) этапе, а второй является процедурой преобразования форм представления моделей. Это позволяет разработать и использовать различные компьютерные программы автоматизации составления уравнений по схемам.
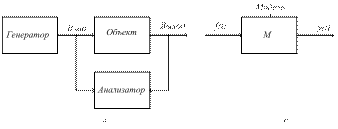
Экспериментальный способ применяется, когда свойства объекта изучены в недостаточной степени либо слишком сложны для аналитического описания. Он заключается в активных экспериментах над объектом или пассивной регистрации его поведения в режиме нормальной эксплуатации (рис. 1.19, а).
Рис. 1.19. Экспериментальное исследование (а) и модель «вход-выход» (б)
В результате обработки данных наблюдений получают модели в требуемой форме. Совокупность этих операций носит название «идентификация объекта». В результате идентификации получают модели «вход-выход» (рис. 1.19, б). Очевидно, что получаемая модель зависит не только от свойств объекта, но и от разнообразия входных сигналов.
Поскольку объект на практике не является «черным ящиком», т.е. о нем что-то известно, то есть возможность комбинировать оба способа: вначале аналитически строить структуру модели и определять приближенные значения параметров, а затем обработкой экспериментальных данных уточнять эти значения.
Используются три основных класса структур моделей систем управления:
– с причинно-следственной структурой;
Модели «вход-выход» отображают зависимость поведения системы от входных воздействий при целостном представлении системы (в виде «черного ящика»). Внутренние переменные (переменные состояния) в них выражаются через входные и выходные переменные.
При построении модели системы с раскрытой причинно-следственной структурой объект или систему предварительно расчленяют на элементы направленного действия и рассматривают их как преобразователи сигналов. Элементы выделяются по функциональному признаку: объект управления, измерительные, преобразовательные и усилительные элементы, устройство управления, исполнительный механизм и т.д. Для каждой части строится своя модель, соединением которых, в соответствии с соединением элементов образуется модель системы. Принципиальной трудностью является создание таких моделей систем с контурами: не зная свойств частей, нельзя знать сигналы на входах этих частей, а без этого нельзя идентифицировать сами части.
В иерархическом представлении структурные модели систем представляются уровнями иерархии (интеграции). При этом модели «вход-выход» являются моделями нулевого уровня причинно-следственной интеграции. Разделение модели «вход-выход»на подсистемы приводит к первому уровню причинно-следственной интеграции и т.д. Дальнейшее раскрытие структур подсистем, каждая из которых снова рассматривается как модель «вход-выход», приводит к многоуровневым (иерархическим) моделям. Часто иерархический подход является единственно возможным для проектирования сложных систем. При этом предполагается, что поведение подсистемы L-го уровня полностью объясняется свойствами подсистем непосредственно нижележащего L-1-го уровня.
Модели среды. Среда на входе системы моделируется автономными системами двух типов:
− генераторами типовых воздействий;
− преобразователями типовых воздействий (фильтрами).
В качестве типовых воздействий используются единичные импульсная и ступенчатая функции, «белый шум». Часто используются также случайные входные воздействия. Некоторые из этих воздействий будут рассмотрены далее.
Детальному исследованию перечисленных типов моделей должно предшествовать рассмотрение математического аппарата, применяемого при исследовании моделей. Поэтому рассмотрим математические средства, применяемые при описании систем управления.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Способы построения моделей



До этого мы говорили о том, зачем создаются модели. Здесь мы рассмотрим вопрос о том, из чего они строятся, и эти способы построения моделей будет третьим признаком их классификации.
Т. к. здесь мы рассматриваем модели, сознательно создаваемые человеком, то для их построения у него в распоряжении имеется практически только два типа «материала» – средства окружающего мира и средства мышления. Соответственно и модели делятся на материальные (реальные, вещественные) и абстрактные (идеальные).
Абстрактные модели и роль языка. Начнем с абстрактных моделей. Абстрактные модели создаются средствами мышления. Причем, поскольку нас интересуют абстрактные модели, предназначенные для общения между людьми, остановимся лишь на моделях, создаваемых средствами естественного языка, не рассматривая такие иррациональные формы общения, как гипноз, телепатия и т.п.
Итак, языковые модели. Естественным языком, как известно, можно говорить обо всем, т.е. он является универсальным средством построения любых абстрактных моделей. Эта универсальность обеспечивается возможностью:
— введения в язык новых слов;
— иерархического построения все более развитых языковых конструкций (слово ® предложение ® текст), а также достигается еще и тем, что
— языковые модели обладают неоднозначностью, расплывчатостью.
Свойство неоднозначности, расплывчатости проявляется уже на уровне слов. Действительно, почти каждое слово в любом языке имеет несколько значений (толковый словарь), в каждом языке есть неопределенные слов (типа «много», «несколько» и т.п.), и, кроме того, существует практически бесчисленное множество вариантов соединения слов во фразы. Все это вместе позволяет с достаточной для практических целей точностью отобразить любую ситуацию. Иногда эту расплывчатость языка используют сознательно (юмор, дипломатия, поэзия), в других же случаях она мешает выразиться настолько точно, насколько бы хотелось (тогда говорят — «у меня нет слов», или более глубокое — «мысль изреченная есть ложь»).
И если в обыденном общении расплывчатость языка обычно не мешает, то в науке, когда требуется точное описание явлений, расплывчатость языка становится существенным недостатком, и этот недостаток должен быть устранен. Это обеспечивается созданием т.н. профессиональных языков. Наиболее ярко это видно на примере профессиональных языков конкретных наук, каждая из которых имеет специфическую терминологию.
Существование естественного и профессиональных языков образует иерархию языковых моделей. На верхнем уровне этой иерархии находятся модели, созданные средствами естественного языка, т.к. он является универсальным, на промежуточных уровнях – модели, созданные все более точными профессиональными языками, на нижнем — модели, имеющие максимальную для нынешнего состояния данной отрасли знаний точность. Высшим с точки зрения точности и определенности является язык математики. Математические модели обладают абсолютной точностью, однако, для того чтобы использовать математические модели в какой-то конкретной области, необходимо иметь достаточное количество знаний.
Материальные модели и виды подобия. Перейдем к материальным моделям. Чтобы некая материальная конструкция могла быть отображением оригинала, между ними должно быть подобие. Существует несколько типов такого подобия.
Первый тип подобия называется прямым. Прямое подобие обладает свойством похожести модели и оригинала. К числу таких моделей можно отнести фотографии, модели автомобилей, самолетов, кораблей или гидротехнических сооружений, макеты зданий, куклы, протезы, выкройки и т.п. Только при прямом подобии возможна трудно обнаруживаемая взаимозаменяемость модели и оригинала (например, копии произведений искусства) и даже перемена их местами (натурщик является моделью в работе художника, манекенщица – будущих потребителей одежды, актер – персонажа пьесы и т.п.).
Несмотря на то, что модель при прямом подобии не просто внешне похожа на оригинал, но может быть даже изготовлена из тех же материалов, — все равно она остается только моделью, и при переносе результатов моделирования на натуру ча-

сто возникают достаточно серьезные проблемы.
Пример. Производятся испытания на уменьшенной модели корабля его гидродинамических качеств. При переносе результатов моделирования на натуру встает проблема масштаба, поскольку одна часть условий эксперимента может быть приведена в соответствие с масштабом модели (например, скорость течения), а другая (например, вязкость и плотность воды, сила гравитации, оп-
ределяющие свойства волн) – не может.
В результате задача переноса результатов модельного эксперимента на натуру зачастую является не менее сложной, чем само моделирование, и выгод от похожести модели на оригинал оказывается гораздо меньше, чем при моделировании без нее. Достаточно сказать, что разработана даже специальная теория подобия, позволяющая обосновать прямое подобие модели и оригинала.
Второй тип подобия называют косвенным. Косвенное подобие между оригиналом и моделью не устанавливается специально, а объективно существует в природе. Уже давно было замечено, что многие совершенно, казалось бы, разнородные явления и процессы в природе имеют общие закономерности и описываются одними и теми же уравнениями (т.е. имеют одинаковые или достаточно близкие абстрактные модели). Различие между ними состоит лишь в разной физической интерпретации
переменных, входящих в эти уравнения.
Пример 1. Наиболее известным примером является электромеханическая аналогия, когда некоторые механические процессы вполне могут быть заменены электрическими. В результате оказалось возможным не только заменить громоздкое, дорогое и неудобное моделирование с механическими конструкциями на простые опыты с электрическими схемами, перепробовать множество вариантов, не переделывая конструкцию, но и «проиграть» на модели варианты, в механике пока неосуществимые (непрерывное изменение длин, масс и т.п.).
Пример 2. В описании транспортных потоков на макроуровне широко используется гидродинамическая аналогия, т.е. движение транспортных потоков можно представить как движение жид-
кости в гидросистемах, которые уже достаточно хорошо изучены и описаны.
Третий класс реальных моделей образуют модели, подобие которых оригиналу не является ни прямым, ни косвенным, а устанавливается по соглашению. Такое по-
добие называется условным.
Пример. Примерами условного подобия являются деньги (модель стоимости), удостоверения личности (модель их владельцев), карты (модели местности), разнообразные сигналы (модели со-
Таким образом, модели условного подобия имеют вещественную форму, но абстрактное содержание. И для того, чтобы это содержание не терялось при хранении, передаче от одного человека к другому, необходимо соглашение о том, какое именно состояние объекта-оригинала соответствует данному абстрактному содержанию. Для этого специально разрабатываются правила построения таких моделей и пользования ими.
Знаковые модели и сигналы. Некоторые специфические модели условного подобия стали предметом исследований. Они бывают двух типов. Модели первого типа предназначены для работы в технических устройствах без участия человека, получили название сигналов и изучаются такими науками как радиотехника, теория связи, теория информации и др. (например, сигналы светофора). Надо отметить, что правила построения и использования сигналов, названные кодированием и декодированием, сами стали предметом исследования (криптография).
Несколько с иных позиций рассматриваются модели условного подобия второго типа. Они создаются самим человеком и для себя. Эти модели получили название знаков, а изучающая их наука – семиотика (от греч. «знак»). Причем семиотика изучает не знаки как таковые, а взаимоотношения, возникающие при использовании этих знаков. Это отношения между:
— различными знаками, позволяющими отличать их и строить из них знаковые конструкции все более возрастающей сложности (они получили название синтаксис; греч. «порядок»);
— знаками и тем, что они обозначают (семантика; греч. «обозначение»);
— знаками и теми, кто их использует (прагматика; греч. «действие»).
В заключение следует отметить, что хотя условное подобие в принципе не накладывает никаких ограничений на вид моделей, все равно эти модели должны строить-
ся с учетом особенностей людей, для которых они предназначены.
Пример 1. Знаковые модели для слепых, глухонемых и обычных людей должны быть качественно различными.
Пример 2. Казалось бы, выбор символов для обозначения цифр может быть произвольным, однако арабская символика при вычислениях в настоящее время полностью вытеснила римскую. Это произошло потому, что арабские цифры более удобны при выполнении ручных операций.
По этой же причине на ЭВМ двоичная символика вытеснила десятичную.
Источник
Способы создания моделей
 |  |
| Теоретический –предполагает создание модели на основе известных законов физики, механики, описывающих основные с точки зрения поставленной цели процессы, происходящие в объекте. | Экспериментальный (или идентификация) предполагает построение модели на основе результатов эксперимента, проведенного с реальным объектом. |
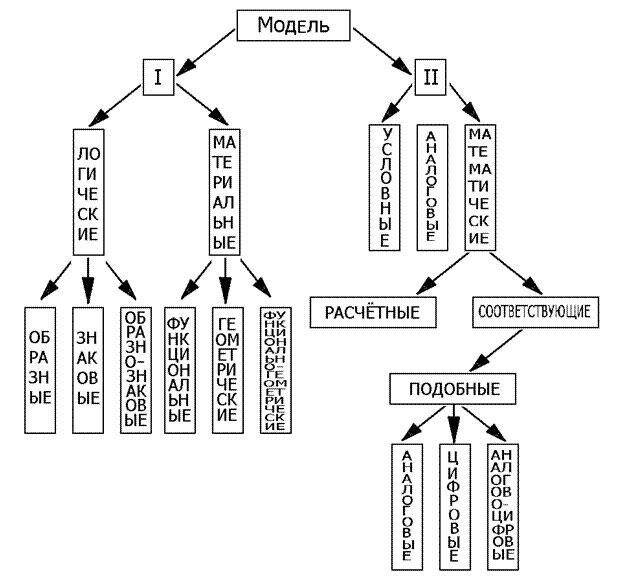 |
Рис.3 Классификация моделей
В основу классификации положены наиболее важные признаки моделей:
1. Закон функционирования и характерные особенности выражения свойств и отношений оригинала;
2. Основания для преобразования свойств и отношений модели в свойства и отношения оригинала.
По первому признаку модели разделяют на логические — образные, знаковые, образно — знаковые и материальные — функциональные, геометрические, функционально — геометрические. Логическиемодели функционируют по законам логики в сознании человека. Материальные — по объективным законам природы.
* Образные (иконические) модели — выражают свойства оригинала с помощью наглядных чувственных образов, имеющих прообразы среди элементов оригинала или объектов материального мира. Пример, частицы газа в виде упругих шаров (кинетическая теория газа).
* Знаковые (символические) модели — выражают свойства оригинала с помощью условных знаков и символов. Пример, математические выражения и уравнения, физические и химические формулы и т.п.
* Образно — знаковые модели — обладают признаками образных и знаковых моделей. Пример: схемы, графики, чертежи, графы, структурные формулы, иероглифы и т.п.
* Функциональные модели — отражают основные функциональные свойства оригинала. Пример, моделью маятника, совершающего колебательное движение, может служить RLC-цепочка.
* Геометрические модели — отражают пространственные свойства оригинала. Пример, глобус.
* Функционально — геометрические модели — отражают одновременно функциональные и пространственные свойства оригинала. Пример, макет самолета в аэродинамической трубе.
В зависимости от физической однородности и разнородности с оригиналом функциональныеи функционально — геометрические модели разделяются на физические и формальные. Пример, работу электрического генератора необходимо исследовать на активно — емкостной потребитель, подключение к которому по каким-либо причинам невозможно, потребитель можно заместить на последовательную цепь из резистора и конденсатора. В этом случае эта цепь является физической моделью потребителя. Если оригинал — маятник, то электрический колебательный контур является его формальной моделью.
По второму признаку модели делятся на условные, аналогичные и математические.
* Условные модели — выражают свойства и отношения оригинала на основании принятого условия (соглашения). Сходство с оригиналом у таких моделей может совершенно отсутствовать. К ним относятся все знаковые и образно — знаковые модели.
* Аналогичные модели — обладают сходством с оригиналом, достаточным для перехода к оригиналу на основании умозаключения по аналогии, т.е. на основании логического вывода, что, оригинал, возможно, обладает некоторым признаком, имеющимся у модели, так как другие признаки оригинала сходны с признаками модели. Пример, все виды макетов кораблей, самолетов и т.д.
* Математические модели – модели, в которых основные функциональные свойства объекта заменяются математическими выражениями. Они обеспечивают переход к оригиналу, фиксацию и исследование его свойств и отношений с помощью математических методов.
Математические модели делятся на расчетные и соответствующие:
Расчетные — выражают свойства и отношения оригинала с помощью математических представлений — формул, уравнений, графиков, таблиц, операторов, алгоритмов и т.д. Пример, объект Z=X*Y – модель выходная координата.
Соответствующие – модели, в которых переменные величины модели связаны с соответствующими переменными величинами оригинала определенными математическими зависимостями. Пример, если две функции Z=XY и z=x+y, а также их независимые переменные связаны соотношениями x= lgX, y =lgY, z = lgZ, то каждый из таких объектов может служить соответственной моделью другого.
Математические модели имеют признаки условных моделей и могут обладать признаками аналогичных.
Среди соответствующих моделей можно выделить важнейший класс – подобные модели, которые как класс формируются на основе теории подобия.
Подобные модели — переменные величины, в которых пропорциональны соответствующим переменным оригинала. Подобные модели также могут быть логическими и материальными. Подобные материальные модели подразделяются на аналоговые (непрерывные), цифровые (дискретные) и аналого-цифровые (комбинированные и гибридные), это зависит от того, какие величины связывает их математическое описание — непрерывные, дискретные или те и другие вместе.
Аналоговые —модели, в которых основные функциональные свойства объекта заменяются подобными функциональными свойствами модели любой природы.
Цифровые — модели, в которых основные функциональные свойства объекта моделируются дискретно.
Аналогово-дискретные –модели, которые сочетают в себе аналоговую и дискретную части (одни свойства объекта выражаются аналоговыми, другие – дискретными моделями).
Подобие оригинала и его материальной модели позволяет использовать последнюю в качестве вычислительного устройства для решения уравнений, описывающих оригинал.
Согласно общей теории моделирования, все вычислительные устройства являются материальными подобными моделями соответствующих материальных или логических оригиналов.
В зависимости от характера математического описания эти устройства могут быть аналоговыми, цифровыми и аналого-цифровыми.
Классификация методов моделирования
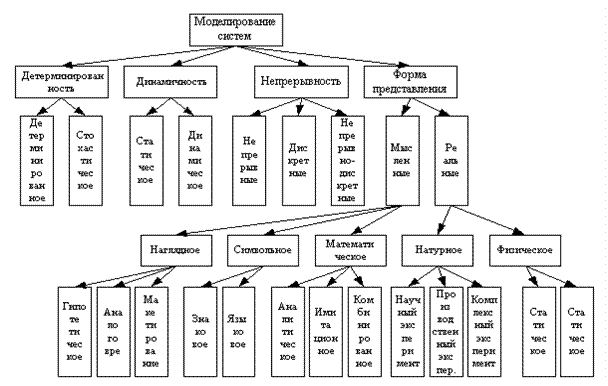 |
Рис. 4 Классификация методов моделирования
Моделирование систем включает в себя модели объекта с одной стороны и способы отражения их функционирования с другой.
По характеру изучаемых процессов моделирование может классифицироваться по следующим признакам: детерминированность, динамичность, непрерывность и форма-представление.
С точки зрения детерминированности различают: детерминированное и стохастическоемоделирование. При детерминированном моделировании используются детерминированные методы без учета случайных воздействий внешней среды. Стохастическое моделирование отображает вероятностные и случайные процессы в объекте. При этом используется математический аппарат статистики и вероятностных процессов.
С точки зрения динамичности разделяют статическое и динамичное моделирование. Динамичное моделирование процессы, происходящие в объекте, рассматривает во времени. Статическое моделирование изучает особые статические режимы, когда процессы, происходящие в объекте, не зависят от времени.
По признаку непрерывности различают: непрерывное, дискретное и непрерывно-дискретное моделирование. Непрерывное моделирование рассматривает процессы, происходящие в объекте, непрерывно в течение всего времени исследования. Математическим аппаратом данного типа моделирования являются дифференциальные уравнения. Дискретное моделирование изучает процессы в определенные моменты времени, математический аппарат – разностные уравнения. Непрерывно-дискретное моделирование сочетает в себе свойства непрерывного и дискретного моделирования.
По формам представления моделирование может быть мысленное (логическое) и реальное (материальное).
Мысленное моделированиеприменяется при исследовании систем, которые по каким-либо причинам не может быть реализовано физически. Мысленное моделирование в свою очередь разбивается на три крупных класса:
Наглядное моделирование — это создание наглядных моделей на базе представлений человека об объекте.
Наглядное моделирование подразделяется на гипнотическое, аналоговое и макетирование.
· Гипнотическое моделирование – это исследование модели в виде черного ящика, при этом структура и функциональные особенности объекта представляются гипотезой. После выдвижения гипотезы она либо принимается, либо нет.
· Аналоговое моделирование применяется в том случае, когда любое функциональное свойство объекта заменяется аналоговым.
· Макетирование применяется в случае, если невозможна физическая реализация объекта. Модель представляет собой полную аналогию с исследуемым объектом, но в другом масштабе.
Символьное моделирование – замена реального объекта неким набором символов (любому объекту ставится в соответствие символ). Выделяют языковое и знаковое моделирование.
· При знаковом моделировании вводятся символьные обозначения определенных понятий, однородные понятия объединяются в отдельные множества. Все знаковое моделирование сводится к теории множеств и операциям между ними.
· При языковом моделировании объекту и процессам, происходящим в нем, ставится в соответствие тезаурус – язык, лишенный двусмысленности, т.е. его символика похожа на символику нашего языка, но все однозначно.
Математическое моделирование подразделяется на аналитическое, имитационноеи комбинированное.
· Аналитическое моделирование – определенному объекту ставится в соответствие система уравнений и методы ее решения (высшая математика). Применяется при исследовании относительно несложных систем, к которым относится САУ.
· Имитационное моделирование – отдельные свойства объекта имитируются конкретными математическими способами (нет конкретной модели), используется для исследования сложных систем. Как правило, применяется к стохастическим моделям и системам массового обслуживания. Для имитационного моделирования применяется пакет GPSS.
· Комбинированное моделирование – это моделирование, в котором используются элементы аналитического и имитационного.
Реальное моделированиеможет быть натурным и физическим.
Натурное моделирование – это проведение исследований с реальными объектами с последующей обработкой результатов эксперимента.
· производственный эксперимент – воспроизведение на натурном объекте основных режимов производственного процесса для дальнейшего исследования.
· научный эксперимент – воспроизведение на натурном объекте качественно новых режимов, увеличение технических границ.
· комплексный эксперимент – сочетает в себе элементы научного и производственного эксперимента
При постановке научного эксперимента реальный объект используется в качественно новых условиях функционирования или при воздействии новых факторов внешней среды с последующей обработкой результатов.
Физическое моделирование:
· в реальном масштабе времени – осуществляют постановку эксперимента в одинаковых масштабах времени как для объекта, так и для модели.
· в нереальном масштабе времени – при постановке эксперимента масштабы времени для модели и объекта различаются на некоторую величину.
Источник