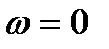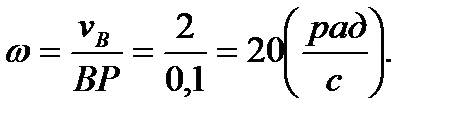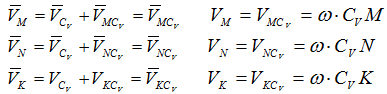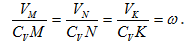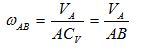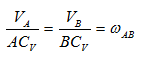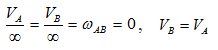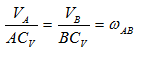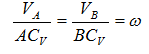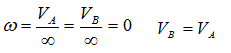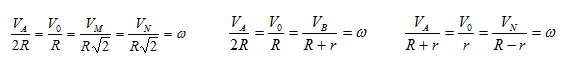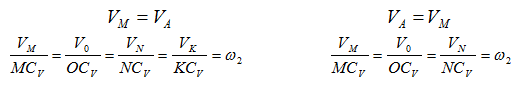Способы построения мгновенного центра скоростей

Основные способы построения МЦС

1. Один способ уже рассмотрен при доказательстве теоремы о существовании МЦС.

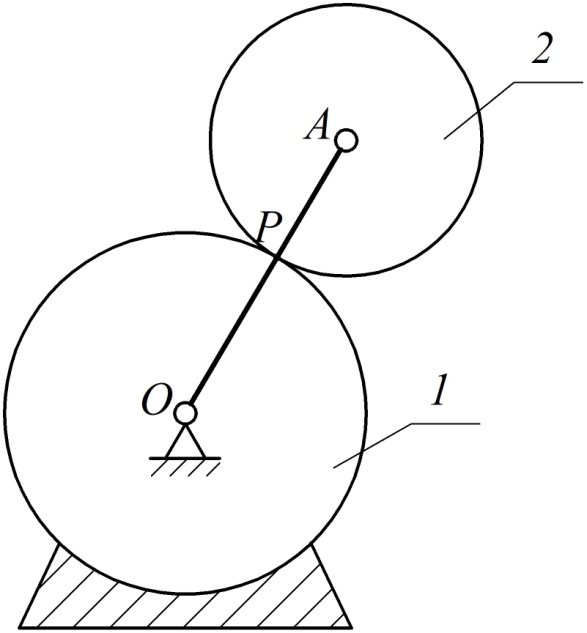
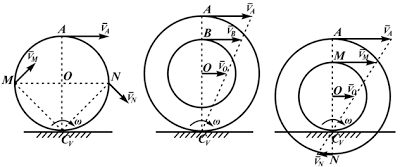
2. Визуальный способ. Иногда сразу удается указать точку плоской фигуры, скорость которой в данный момент времени равна нулю. Например, в случае качения тела по неподвижной поверхности без проскальзывания точка контакта тела с неподвижной поверхностью имеет нулевую скорость и является мгновенным центром скоростей. На рис. 38 точка Р является мгновенным центром скоростей для тела 2.

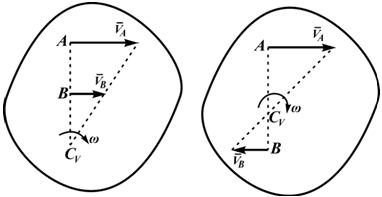
3. Если известны направления скоростей в двух точках тела, то, как видно из рис. 37, мгновенный центр скоростей найдется как точка пересечения перпендикуляров к скоростям этих точек тела. Этот способ нахождения МЦС чаще всего используется на практике. Здесь следует отметить два частных случая.

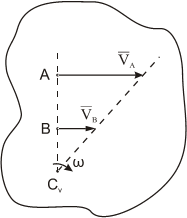
3.а. Если точки лежат на общем перпендикуляре к скоростям этих точек, нужно дополнительно знать величины скоростей. В этом случае МЦС найдется как точка пересечения общего перпендикуляра к скоростям и прямой, проведенной через концы векторов скоростей точек, изображенных в выбранном масштабе (см. рис. 39). Этот способ построения следует из пропорциональности скоростей точек тела расстояниям от этих точек до МЦС (см. формулу (49)).

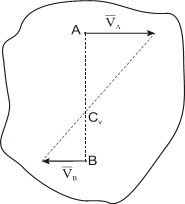
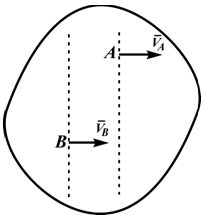
3.б. Если перпендикуляры к скоростям точек тела (случай 3) или общий перпендикуляр к скоростям точек и прямая, проведенная через концы векторов скоростей, (случай 3.а) параллельны, то говорят, что МЦС находится в бесконечности (см. рис. 40).

В этом случае движение тела называют мгновенно-поступательным. При мгновенно-поступательном движении угловая скорость тела равна нулю

и скорости всех точек тела равны по величине и одинаково направлены

Заметим, что при мгновенно-поступательном движении в отличие от поступательного траектории различных точек тела и их ускорения не будут одинаковыми.

Пример 6

Кривошип ОА длиной ОА=0,2 м вращается вокруг неподвижной оси О с угловой скоростью . С помощью шатуна АВ кривошип приводит в движение диск радиуса R=0,1м, катящийся по горизонтальной плоскости без проскальзывания. В положении, указанном на рисунке 41 (когда кривошип вертикален, а шатун горизонтален), найти угловую скорость диска и скорости точек C и D.

Вычислим вначале скорость точки А

Покажем вектор 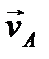на рисунке, направив его перпендикулярно ОА и согласовав по направлению с направлением угловой скорости . Шатун совершает плоское движение. Построим для шатуна АВ мгновенный центр скоростей. Проведем перпендикуляры к скоростям точек А и В (при этом учтем, что скорость точки В направлена горизонтально, так как траекторией этой точки является горизонтальная прямая). Проведенные перпендикуляры параллельны. Следовательно, мгновенный центр скоростей шатуна находится в бесконечности и скорости точек А и В равны по величине и одинаково

направлены. Покажем вектор на рисунке. Так как диск катится без проскальзывания, то его МЦС находится в точке контакта с опорной поверхностью (точка Р на рисунке). Найдем теперь угловую скорость диска

Покажем ее на рисунке, согласовав по направлению со скоростью точки В. Далее легко вычислить величины скоростей точек C и D диска

Покажем векторы и на рисунке, направив их перпендикулярно отрезкам СР и DР и согласовав по направлению с ω.

Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой.

Источник

iSopromat.ru

Мгновенным центром скоростей (МЦС) при плоскопараллельном движении называют связанную с плоской фигурой точку, скорость которой в данный момент равна нулю.

Такая точка существует в каждый момент времени.

Теорема Эйлера-Шаля доказывает, что любое непоступательное перемещение фигуры в плоскости можно осуществить поворотом вокруг некоторого неподвижного центра.

Рис. 1.5 т C — Мгновенный центр скоростей

В соответствии с этим легко доказывается, что при плоскопараллельном движении в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нолю. Эту точку называют мгновенным центром скоростей (МЦС). В учебниках эту точку пишут с индексом V, например P_V, C_V.

При определении положения МЦС скорость любой точки может быть записана: V_M=V_CV+V_MCV, где точка С_V выбрана за полюс.

Поскольку это МЦС и V_CV=0, то скорость любой точки определяется как скорость при вращении вокруг мгновенного центра скоростей.

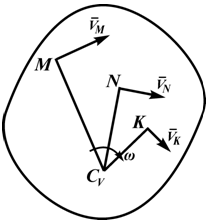
Из рис. 1.5 видно, что мгновенный центр скоростей лежит в точке пересечения перпендикуляров, проведенных к скоростям точек, при этом всегда справедливо соотношение

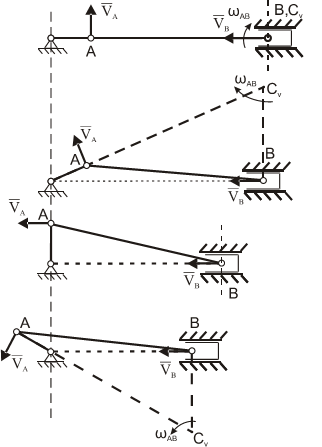
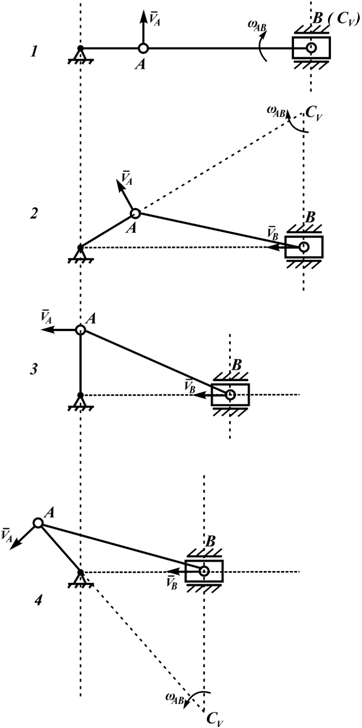
На нижеприведенных рисунках показаны примеры определения положения мгновенного центра скоростей и приведены формулы для расчета скоростей точек.

1. С_V совпадает с точкой В V_B=0. Шатун АВ вращается вокруг точки В
   
2. 
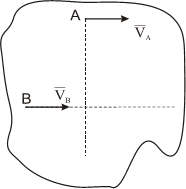
3. МЦС лежит в «бесконечности»
   
4. 

В этом случае МЦС находится в “бесконечности”, т.е

Формулы справедливы при отсутствии проскальзывания в точке СV.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

Набор студента для учёбы

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Источник

iSopromat.ru

Рассмотрим формулы и примеры определения положения мгновенного центра скоростей (МЦС) для различных твердых тел и механизмов при плоскопараллельном движении.

Теорема Эйлера-Шаля доказывает, что любое непоступательное перемещение фигуры в плоскости можно осуществить поворотом вокруг некоторого неподвижного центра.

В соответствии с этим легко доказывается, что при плоскопараллельном движении в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нулю.

Эту точку называют мгновенным центром скоростей (МЦС). В учебниках эту точку пишут с индексом V, например P_V, C_V.

При определении положения МЦС скорость любой точки может быть записана: V_M = V_Cv + V_MCv , где точка C_V выбрана за полюс. Поскольку это МЦС и V_Cv=0, то скорость любой точки определяется как скорость при вращении вокруг мгновенного центра скоростей:

Из рисунка 2.16 видно, что МЦС лежит в точке пересечения перпендикуляров, проведённых к скоростям точек, при этом всегда справедливо соотношение:

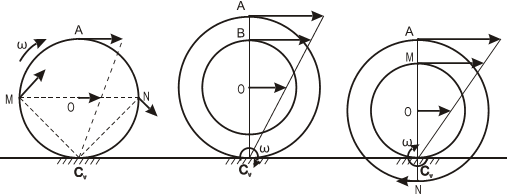
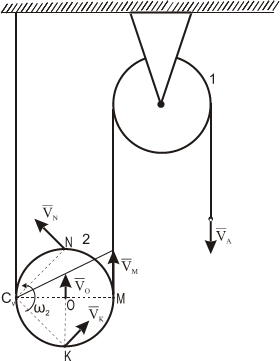
На рисунке 2.17 показаны примеры определения положения МЦС детали кривошипно-шатунного механизма и приведены формулы для расчета скоростей точек.

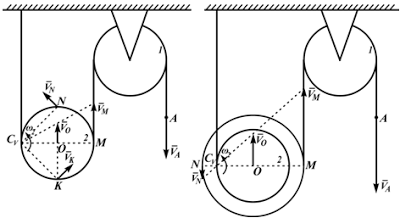
На рисунках 2.18 — 2.21 приведены примеры определения положения МЦС.

В этом случае МЦС находится в «бесконечности», т.е.

1. V_A/2R=V₀/R=V_M/(R√2)=ω,
2. V_A/2R=V₀/R=V_B/(R+r)=ω,
3. V_A/(R+r)=V₀/r=V_N/(R-r)=ω

Формулы справедливы при отсутствии проскальзывания в точке C_V.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

Набор студента для учёбы

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Источник

37 Мгновенный центр скоростей и способ его нахождения

Мгновенный центр скоростей и способ его нахождения

Из построения плана скоростей вытекает, что в каждый момент существует точка плоской фигуры, скорость которой равна нулю. Этой точке плоской фигуры соответствует полюс на плане скоростей.

Точкой плоской фигуры, скорость которой в данный момент времени равна нулю, называется мгновенным центром скоростей (МЦС). Условимся обозначать его буквой Р. Положение мгновенного центра скоростей можно определить двумя геометрическими способами: 1) по заданной скорости какой – либо точки плоской фигуры и мгновенной угловой скорости вращения этой фигуры; 2) по известным направлениям скоростей двух точек плоской фигуры.

Первый способ. Пусть заданная скорость υ_А точки А плоской фигуры и мгновенная угловая скорость ω вращения фигуры вокруг точки А (рис. 73, а). Тогда по формуле (ІІ.95) получим для мгновенного центра скоростей Р

Но, по определению точки Р , υ_Р=0. Следовательно,

Рекомендуемые файлы

Откуда расстояние мгновенного центра скоростей Р от точки А равно

АР =

Итак, мгновенный центр скоростей находится на перпендикуляре, проведенном из начала вектора скорости заданной точки А на расстоянии, равном отношению модуля скорости заданной точки к модулю угловой скорости.

Второй способ. Пусть заданы направления скоростей двух точек А и В (рис. 73, б) движущейся плоской фигуры. Требуется определить положение мгновенного центра скоростей. Выбирая в качестве полюса точку Р, по формуле (ІІ.95) получим

Люди также интересуются этой лекцией: 20.4 Сорокин.

т.е. скорости точек А и В можно рассматривать как скорости в их вращательном движении вокруг мгновенного центра скоростей Р. Так как эти скорости перпендикулярны к отрезкам, соединяющим заданные точки с мгновенным центром скоростей Р, то мгновенный центр скоростей находится в точке пересечения перпендикуляров, проведенных из начала векторов скоростей двух точек плоской фигуры,

Следовательно, величины скоростей двух точек тела при плоско-параллельном движении относятся между собой как их расстояния от мгновенного центра скоростей.

Источник