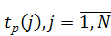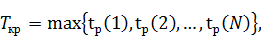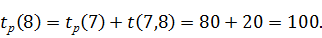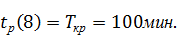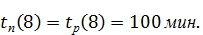- График линейной функции (ЕГЭ 2022)
- График линейной функции — коротко о главном
- Построение графика линейной функции
- Пример неявно заданной линейной функции
- Что такое угловой коэффициент
- 4 примера построения графика линейных функций
- Способы построения линейной функции
- Линейный график и способы его построения
График линейной функции (ЕГЭ 2022)
Чтобы понять то, что здесь будет написано, тебе нужно хорошо знать, что такое линейная функция.
Начнем с небольшой проверки:
Если хоть один вопрос вызвал затруднения, прочти тему «Линейная функция».
Приступим к покорению линий и графиков!
График линейной функции — коротко о главном
График линейной функции – прямая линия. Прямую можно провести через две точки.
Чтобы построить график линейной функции вида y=kx+b, нужно:
- вычислить координаты любых двух точек (взять любые два значения аргумента x и вычислить соответствующие два значения y,
- для каждой пары ( x;y ) найти точку в системе координат, и провести прямую через эти две точки.
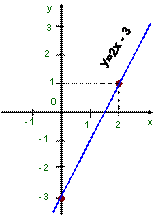
Рассмотрим пример для функции \( y=2x+1\):
Проще всего найти функцию, если аргумент: \( x=0:y\left( 0 \right)=2\cdot 0+1=1\).
Итак, первая точка имеет координаты \( \left( 0;1 \right)\).
Теперь возьмем любое другое число в качестве \( x\), например, \( x=1:y\left( 1 \right)=2\cdot 1+1=3\).
Вторая точка имеет координаты \( \left( 1;3 \right)\).
Угловой коэффициент \( \displaystyle k\) – это тангенс угла наклона прямой.
Для его нахождения выберем две точки \( \displaystyle A\) и \( \displaystyle B\) на графике и построим прямоугольный треугольник с гипотенузой \( \displaystyle AB\)
\( \displaystyle k=tg\alpha =\frac
Построение графика линейной функции
Итак, ты уже умеешь обращаться с линейной функцией, анализировать ее график и строить его по точкам. Кстати, сколько нужно точек, чтобы построить график линейной функции?
Скажу сразу, эта тема настолько простая, что много нового ты здесь не выучишь. Но ты научишься не теряться во всяких нестандартных ситуациях.
Итак, дамы и господа, линейная функция:
Построение графика линейной функции: ты берешь два каких-либо икса, (например, \( \displaystyle 0\) и \( \displaystyle 1\)), подставляешь их в формулу, находишь соответствующие игреки.
Затем отмечаешь эти две точки на координатной плоскости, прикладываешь линейку, и график готов. Просто и быстро, и ничего выдумывать не надо.
Но бывает, что функция задана по-другому, например, неявно. Сейчас разберем, как быстро справляться с такими ситуациями.
Пример неявно заданной линейной функции
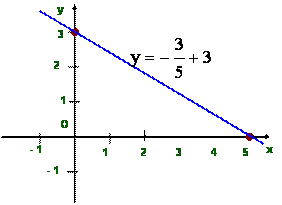
Постройте график уравнения \( \displaystyle 2y+3x=6\).
Ну а что тут сложного? Чтобы произвести построение графика линейной функции выражаем y и строим по точкам.
Это да, но можно сделать проще и интересней!
Выясним, в какой точке эта прямая будет пересекать ось \( \displaystyle Ox\).
Что характерно для этой точке? Правильно, \( \displaystyle y=0\). Так и пишем:
\( \displaystyle 2\cdot 0+3x=6\text< >\Rightarrow \text< >x=2\)
А теперь проделаем то же самое с другой осью: в какой точке график пересекает ось \( \displaystyle Oy\)?
\( \displaystyle x=0\text< >\Rightarrow \text< >2y+3\cdot 0=6\text< >\Rightarrow \text< >y=3\)
Бум! Вот и они – две точки графика. Осталось только приложить линейку:
Согласись, это было быстро и просто!
А теперь сам:
Ладно, а как еще можно задать функцию?
Ну, например словесно:
Прямая проходит через точку \( \displaystyle A\left( 2;3 \right)\), а ее угловой коэффициент равен \( \displaystyle 0,75\).
Ну что же, вспоминаем: что такое угловой коэффициент?
Что такое угловой коэффициент
Это, с одной стороны, коэффициент при \( \displaystyle x\), а с другой – это тангенс угла между прямой и осью \( \displaystyle Ox\).
Вот это мы и используем когда делаем построение графика линейной функции: ставим точку \( \displaystyle A\), и рисуем прямоугольный треугольник так, что один его катет параллелен оси \( \displaystyle Ox\), а другой – перпендикулярен.
При этом второй катет должен быть ровно в \( \displaystyle 0,75\) раз больше первого.
Очень удобно в этом случае, чтобы первый катет был равен \( \displaystyle 4\), тогда второй будет равен \( \displaystyle 3\):
4 примера построения графика линейных функций
Пример №1
Прямая, уравнение которой имеет вид \( y=-2x+b\) (\( b\) неизвестно), проходит через точку \( M\left( 1;2 \right)\). Постройте ее.
Должно получиться вот так:
Пример №2
Произведи построение графика линейной функции и найди уравнение прямой, проходящей через точку \( A\left( 3;1 \right)\) и параллельной прямой \( y=-1,5x+1\).
Строить график прямой \( y=-1,5x+1\) нельзя.
О, это что-то новенькое. Про параллельность прямых мы еще не учили.
Но как обычно, все просто. Нарисуем несколько параллельных прямых на координатной плоскости:
Что у них общего? Вообще, какие параметры важны для графиков? Конечно же, коэффициенты \( k\) и \( b\).
И сразу становится ясно: раз \( k\) отвечает за наклон, а наклон у них одинаковый (это же параллельные прямые, а ось \( Ox\) – секущая), значит, у них одинаковый коэффициент \( k\)!
Вернемся к задаче. Напомню условие:
Произведи построение графика линейной функции и найди уравнение прямой, проходящей через точку \( A\left( 3;1 \right)\) и параллельной прямой \( y=-1,5x+1\).
Итак, угловой коэффициент нашей прямой \( y=-1,5x+1\) равен угловому коэффициенту прямой , то есть \( -1,5\). Теперь задача становится точь в точь как мы решали до этого:
Источник
Способы построения линейной функции



І. Способ построения:
Для построения графика линейной функции необходимо знать координаты двух точек. Отложив их на координатной плоскости и соединив, мы получим график данной функции.
Для построения графика прямой пропорциональности достаточно найти всего одну точку, так как второй будет точка начала координат (0,0).
Построим две функции у = 2х-3 и у = 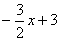
| у = 2х–3 | ||
| х | ||
| у | у=2*0–3= –3 | у=2*2–3=1 |
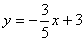 | ||
| х | ||
| у | у = 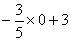 =3 =3 | у = 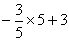 =0 =0 |
При составлении таблиц желательно подбирать значения х такие, при которых удобно было бы вычислять у. Так для первой функции большого значения выбор х не имеет, просто берём маленькие значения, а для второй функции число 5 при умножении сокращается со знаменателем дроби и сводит вычисление у к устному счёту (рис.2).
Иногда удобно наоборот подбирать значения у и находить х.
ІІ. Способ построения:
Графиком функции у = ах + b служит прямая, параллельная линии у = ах, сдвигом на b единиц вверх при b>0 или вниз при b
Для функции у = 2х -3 нужно построить прямую у =2х и параллельно её сдвинуть вниз на 3 единицы (b= -3) (рис.3).
Соответственно, для функции у = 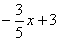
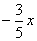
Источник
Линейный график и способы его построения
Сетевой график дает общее представление о структуре комплекса работ и технологической последовательности их выполнения.
Недостатком сетевого графика является то, что он не дает четкого преставления о взаимном расположении работ во времени, что затрудняет нахождение критического пути и оптимизации сетевого графика.
Это недостаток отсутствует у линейного графика, или диаграммы Ганта. Элементами линейного графика являются работы, которые изображаются в системе координат (номер работы – время выполнения).
Линейный график строится по следующему правилу:
· работы изображаются на графике линиями (прямоугольниками), длина которых пропорциональна их длительности;
· работы изображаются на графике, если построены все работы, непосредственно ей предшествующие;
· момент начала выполнения данной работы определяется моментом окончания выполнения всех непосредственно предшествующих ей работ.
Пример 7.4.Построить линейный график по данным табл. 7.1
Решение. По изложенным выше правилам построим линейный график.
0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 29
| 1.1 |
Время t, y.e.
После построения линейного графика технического обслуживания автомобиля перенумеруем работы. Теперь в отличие от нумерации работ в табл. 7.1., например, работа 5 имеет код 1.2.
Для всех работ (i, j) на основе ранних и поздних сроков свершения событий можно определить показатели, которые являются также основными параметрами линейного технологического графика:
· ранний срок начала события
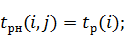
· ранний срок окончания события показывает, через какое время после начала выполнения комплекса работ будет завершена рассматриваемая j-я работа, если все работы будут выполняться в соответствии с графиком,
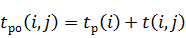
При описанном выше порядке построения линейного графика ранние сроки завершения работ легко определяются из графика: они соответствуют моментам времени окончания работ (определяются путем проектирования работ на временную ось);
· поздний срок начала события
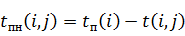
· поздний срок окончания события
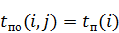
− максимально (предельно допустимый) срок завершения рассматриваемой работы, не приводящий к увеличению критического пути.
Он показывает, через какое время после начала выполнения комплекса работ должна быть завершена данная работа, чтобы общая продолжительность работ не увеличилась.
Заметим, что значения 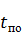
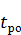
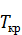
· длина критического пути 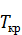
где N – общее число работ в комплексе;
· полный резерв времени выполнения работы 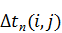
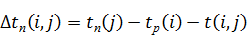
Пример 7.5.Рассчитать параметры линейного графика, представленного в примере 7.4.
Решение. В соответствии с рисунком определим ранний и поздний сроки окончания работы. Ранний срок окончания работы характеризует правый срез прямоугольника (работы).
Если работа выполняется не параллельно с другими работами, то поздний срок окончания работы равен раннему сроку.
Поздний срок окончания работы, не равный раннему сроку, можно указать только для тех работ, которые на линейном графике выполняются параллельно, например работы 2 и 3.
В этом случае без ущерба для величины критического пути можно увеличить продолжительность работы 2. То есть поздний срок окончания работы 2 соответствует времени 15 y.e.
Резерв времени легко определяется как разность последнего и раннего сроков окончания работы.
Результаты расчета сведем в таблицу 7.3.
| Номер работы | Код работы | Продолжительность работы t(i), y.e. | Ранний срок окончания работы 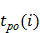 , y.e. , y.e. | Поздний срок окончания работы 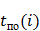 ,y.e. ,y.e. | Резерв времени 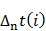 , y.e. , y.e. |
| 1.1 | |||||
| 2.1 | |||||
| 2.2 | |||||
| 2.3 | max <21,16>=21 | ||||
| 1.2 |
Как очевидно из таблицы, длина критического пути равна раннему сроку выполнения работы 1.2 и составляет 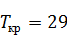
После определения параметров линейного графика строится критический путь. Признаком принадлежности i-й работы критическому пути является равенство 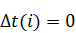
Таким образом, более наглядное представление работ во времени делает процесс оптимизации линейного графика более легким по сравнению с сетевым графиком.
В рассматриваемом примере критический путь проходит через работы 1.1, 2.2, 2.3, 1.2.
Так как работа 2.1 имеет резерв 5 y.e. времени, то можно попытаться привлечь на это время освободившегося специалиста для выполнения работы 2.2, что, скорее всего, сократит время ее выполнения. В этом случае можно ожидать сокращения критического времени выполнения работ при декларировании и выпуске товаров.
Пример 7.6.Необходимо осуществить таможенный контроль представленных деклараций и принять решение о выпуске товаров.
Перечень событий, а также данные о продолжительности работ (в мин.) приведены в таблицах 7.4 и 7.5.
| Шифр события | Описание события | Предшествующие события |
| Начало (прием и регистрация ДТ) | ||
| Документальный контроль, представленный декларантом документов и сведений | ||
| Проверка зарегистрированной ДТ на риски | ||
| Представление отметок о результатах документального контроля в ДТ и других документах | 2,3 | |
| Применение мер по минимизации рисков | 2,3 | |
| Заполнение отчета о результатах применения мер по минимизации рисков | ||
| Проверка соблюдения условий выпуска | 4,6 | |
| Конец (выпуск товаров) |
| Номер работы | Продолжительность работы, мин. |
| 1,2 | |
| 1,3 | |
| 2,4 | |
| 2,5 | |
| 3,4 | |
| 3,5 | |
| 4,7 | |
| 5,6 | |
| 6,7 | |
| 7,8 |
Определить основные параметры сетевого графика.
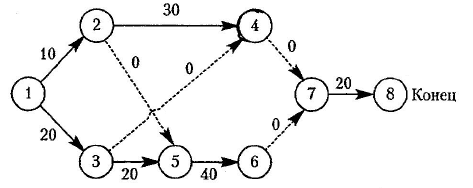
Решение. По данным таблиц составим сетевой график.
Для сетевого графика полными путями будут:
путь 1 → 2 → 4 → 7 → 8 продолжительностью 10 + 30 + 0 + 20 = 60 мин;
путь 1 → 2 → 5 → 6 → 7 → 8 продолжительностью 10 + 0 + 40 + 0 + 20 = 70 мин;
путь 1 → 3 → 4 → 7 → 8 продолжительностью 20 + 0 + 0 + 20 = 40 мин;
путь 1 → 3 → 5 → 6 → 7 → 8 продолжительностью 20 + 20 + 40 + 0 + 20 = 100 мин.
Последний путь имеет наибольшую продолжительность и является критическим. Продолжительность критического пути составляет 100 мин. Быстрее работу выполнить нельзя, так как для достижения завершающего события критический путь надо пройти обязательно.
Расчет параметров сетевого графика:
При определении ранних сроков свершения событий 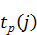
Для начального события j = 1, очевидно, 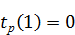
Для j = 2: 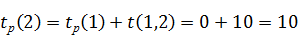
Для j = 3: 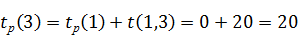
Для j = 4: 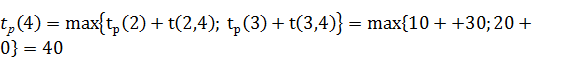
Аналогично определяем ранние сроки для остальных событий сети:
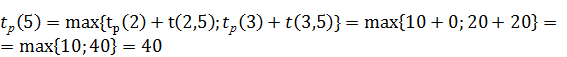
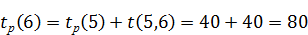
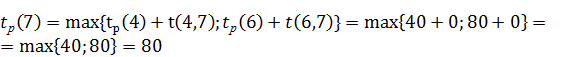
Длина критического пути равна раннему сроку свершения завершающего события 8
Найденные параметры сведем в таблицу 7.6.
| Номер работы | Сроки свершения события, мин. | Резерв времени 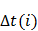 ,мин. ,мин. |
ранний 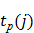 , мин , мин | поздний 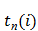 , мин. , мин. |
В этой таблице при определении поздних сроков свершения событий 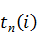
Для i = 8 (завершающего события) поздний срок свершения события должен равняться его раннему сроку (иначе изменится длина критического пути):
Для i = 7: 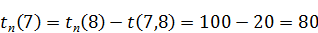
Для i = 6: 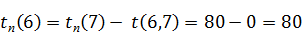
Для i = 5: 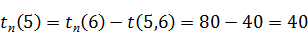
Для i = 4: 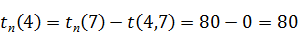
Для i = 3: 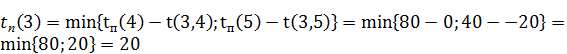
Для i = 2: 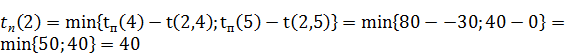
Для i = 1: 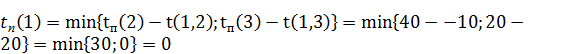
По формуле (7.3) определяем резервы времени i-го события:
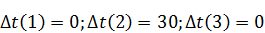
Резерв времени события 2 составляет 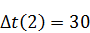
Анализируя последнюю таблицу, видим, что не имеют резервов времени события 1, 3, 5, 6, 7, 8. Эти события и образуют критический путь.
Расчет параметров линейного технологического графика:
Вычисление временных параметров работы (i, j) покажем на примере работы (2,4).
Ранний срок начала работы вычисляется по формуле (7.4): 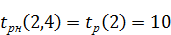
Ранний срок окончания работы вычисляется по формуле (7.5): 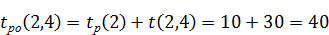
Поздний срок начала работы вычисляется по формуле (7.6): 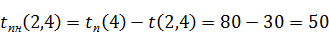
Поздний срок окончания работы: 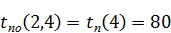
Таким образом, работа 2,4 должна начаться в интервале (10, 50) и окончиться в интервале (40, 80) от начала выполнения работы.
Полный резерв времени работы (2, 4) вычисляется по формуле (7.8): 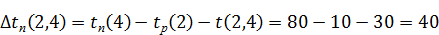
Результаты вычислений сведем в таблицу.
| Работа (i, j) | Продолжительность работы (i, j), мин. | Сроки начала и окончания работы, мин. | Полный резерв времени 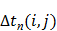 мин. мин. |
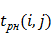 | 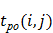 | 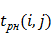 | 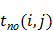 |
| (1, 2) | |||
| (1, 3) | |||
| (2, 4) | |||
| (2, 5) | |||
| (3, 4) | |||
| (3, 5) | |||
| (4, 7) | |||
| (5, 6) | |||
| (6, 7) | |||
| (7, 8) |
Покажем на примере работы (2, 4), что полный резерв времени работы равен резерву времени максимального из путей, проходящих через эту работу.
Этим резервом можно располагать при выполнении данной работы, если ее начальное событие свершится в самый ранний срок, и можно допустить свершение ее конечного события в самый поздний срок.
Важным свойством полного резерва времени работы является то, что он принадлежит не только этой работе, но и всем полным путям, проходящим через нее.
Через работу (2, 4) проходит 1 полный путь: 1 → 2 → 4 → 7 → 8 продолжительностью t = 60 мин. Его резерв 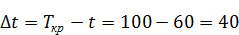
Как видим, полный резерв времени работы (2, 4) равен резерву времени максимального (и единственного) полного пути, проходящего через эту работу.
Если увеличить продолжительность работы (2, 4) на 40 мин., то полностью будет исчерпан резерв времени этого пути, т.е. этот путь станет также критическим.
Источник