Способы построения графиков тригонометрических функций проект

Проект. Построение графиков тригонометрических функций.

В данном проекте представлена компъютерная программа. позволяющая строить графики тригонометрических функций с произвольным аргументом и коэффициетом.

Просмотр содержимого документа
«Проект. Построение графиков тригонометрических функций.»

Проект по алгебре на тему:

их свойства и графики

Ученика 10 Б класса

• Дать определение данных функций
• Рассмотреть графики функций
• Рассмотреть свойства каждой функции
• Дать алгоритм построения графиков
• Создать продукт – программу, строящую график функций вида y=sin(x), y=cos(x)

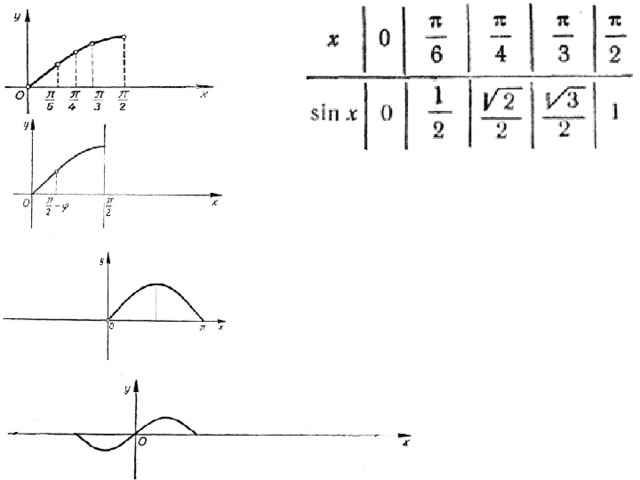
Синусом аргумента х (sin(x)) называется ордината точки пересечения окружности единичного радиуса с центром в точке (0;0) и луча, выходящего из начала координат и составляющего с осью ОХ угол х.

• Составить таблицу значений
• Соединить полученные точки
• Построим на [ π/2 ,π ] путем симметричного отображения графика этой функции на [0 , π/2 ]
• По свойству нечетности функции строим график этой функции в интервале [— π , 0]
• Полученную кривую, продолжить влево и вправо периодически с периодом 2π.

Косинусом аргумента х (cos(x)) называется абсцисса точки пересечения окружности единичного радиуса с центром в точке (0;0) и луча, выходящего из начала координат и составляющего с осью ОХ угол х.

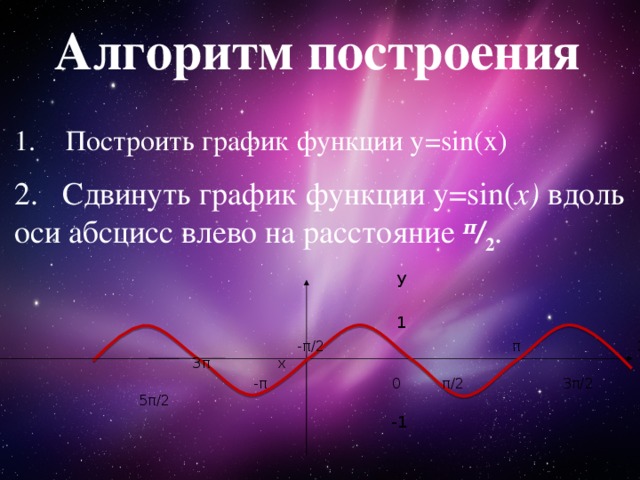
• Построить график функции y=sin(x)

2. Сдвинуть график функции у=sin( x) вдоль оси абсцисс влево на расстояние π / 2 .

В результате проделанной работы на основе предоставленных теоретических материалов был создан продукт – компьютерная программа, способная строить графики рассматриваемых ранее функций.

Источник

Тригонометрические функции и их графики Проектная работа по теме: — презентация

Презентация была опубликована 8 лет назад пользователемwiki.kamgpu.ru

Похожие презентации

Презентация на тему: » Тригонометрические функции и их графики Проектная работа по теме:» — Транскрипт:

1 Тригонометрические функции и их графики Проектная работа по теме:

2 Вопросы проекта Что такое синус? Что такое косинус? Что такое тангенс? Что такое котангенс? Как выглядят графики этих функций? Как построить сложные графики этих функций?

3 Функция y=sin x, график и свойства. 1)D(y)= 2)E(y)= 3) 4)sin(-x)=-sin x 5)Возрастает на Убывает на 6)Периодичная

4 Знаки синуса 1.С инус равен нулю при, где n — любое целое число; 2.Синус положителен при, где n — любое целое число; 3.С инус отрицателен при, где n — любое целое число.

5 Синусоида у 1 -π/2 π 2π 3π х -π 0 π/2 3π/2 5π/2

6 у = sin(x+a) y = sin(x+π/6) y 1 -π π 2π х Примеры

7 у = sinx + a 1)y= sin x + 1; 2)y= sin x — 2 y 1 x’ -π 0 π 2π x -2 x» y= sin x + 1 y= sin x — 2

8 Построение графиков y=sin(x+m)+n 1)y= sin x ; 2)y= sin(x+π/6); 3)y= sin(x-π/3); 4)y= sinx+1; 5)y= sinx-3/2 y 1 -π 0 π 2π 3π x

9 Функция y = cos x, её свойства и график. 1)D(y)= 2)E(y)= 3) 4)cos(-x)=cosx 5)Возрастает на Убывает на 6)Периодична

10 Знаки косинуса 1.косинус равен нулю при 2.косинус положителен при 3. косинус отрицателен при где n — любое целое число.

11 y= cos x у 1 -π/2 π 2π 3π х -π 0 π/2 3π/2 5π/2 Примеры

12 Построение графиков y = cos(x+m)+n 1)y=- cos x; 2)y=cos(x-π/4)+1,5 y 0 x y=- cos x y=cos(x-π/4)+1,5

13 Наибольшее и наименьшее значения функции на промежутке 1 y=sin x на [-2π/3;π/6] Ответ:

14 -π-ππ 1 у х -3π/2 3π/2 y = cos x на (π/3;2π/3] Ответ: Наибольшее и наименьшее значения функции на промежутке

15 Построение графиков y=k · sin x и y=k · cos x. 1)y=1/2sinx; 2)y=2,5cosx. y 2,5 1 x -2,5

16 Функция y = tg x, её свойства и график 1.D(y)= 2.E(y)= 3.tg(-x)=-tgx 4.Возрастает на 5.Периодичная 1

17 Знаки тангенса 1.равен нулю, когда синус равен нулю, то есть при, где n — любое целое число. 2.положителен, когда синус и косинус имеют одинаковые знаки. Это бывает только в первой и в третьей четвертях, то есть при где а- любое целое число. 3.отрицателен, когда синус и косинус имеют разные знаки. Это бывает только во второй и в четвертой четвертях, то есть при где а — любое целое число.

19 y = tg x y=tg(x-π/2) 1 Примеры

20 1.D(y)= 2.E(y)= 3.ctg(-x)=-ctgx 4.Убывает на 5.Периодичная

21 Знаки котангенса 1.равен нулю, когда косинус равен нулю, то есть при 2.положителен, когда синус и косинус имеют одинаковые знаки. Это бывает только в первой и в третьей четвертях, то есть при 3.отрицателен, когда синус и косинус имеют разные знаки. Это бывает только во второй и в четвертой четвертях, то есть при.

22 Вывод В ходе исследования были рассмотрены все основные тригонометрические функции, были рассмотрены их основные функции, графики данных функций и рассмотрены более сложные графики функций.

Источник

Индивидуальный проект на тему «Построение сложных тригонометрических графиков»

Министерство образования и молодежной политики Ставропольского края

Государственное бюджетное профессиональное образовательное учреждение

Георгиевский региональный колледж «Интеграл»

По дисциплине « Математика: алгебра, начала математического анализа, геометрия»

На тему: «Построение сложных тригонометрических графиков»

Выполнила студентка группы ДУ-61, обучающаяся по специальности

«Документационное обеспечение управления и архивоведение »

Куренкова Надежда Алексеевна

Руководитель: преподаватель Серкова Н.А.

Дата сдачи: « » 2017г.

Дата защиты: « » 2017г.

Цель: выявление методов построения графиков сложных тригонометрических функций.

проанализировать литературу по проблеме исследования;

раскрыть сущность методов построения графиков сложных тригонометрических функций;

подобрать и разработать творческие задания, способствующие развитию навыков построения графиков сложных тригонометрических функций

Актуальность исследования: Анализ материала, посвящённого построению графиков сложных тригонометрических функций в учебных пособиях «Алгебра и начала математического анализа» разных авторов, учёт целей изучения данной темы. Атак же обязательных результатов обучения, связанных с рассматриваемой темой.

Основной целью написания данного проекта является представление общих методов построения графиков сложных тригонометрических функций.

Определение синуса, косинуса, тангенса и котангенса.

3. Построение графиков с помощью упрощения формулы. Примеры.

Функция выражает зависимость между переменными величинами. Каждая область знаний химия, физика, биология, социология и др. имеет свои объекты изучения, устанавливает свойства и взаимосвязи между этими объектами в реальном мире. Впервые функция вошла в математику под именем “переменная величина”, в труде французского математика и философа Рене Декарта в 1637 году. Сам термин “функция” впервые встречается в рукописи немецкого математика и философа Г.Лейбница. Леонард Эйлер ввёл принятые сейчас обозначения для функций. Сложный, очень длительный путь развития понятия функции. С ним связаны имена Н.И.Лобачевского, Л.Дирихле, Г. Кантора. Сейчас многие науки берут на вооружение математический аппарат. Такие функциональные зависимости, например, возраст деревьев, развитие папоротника изучает наука биология. Функции помогают описывать процессы механического движения тел небесных и земных. С помощью них учёные рассчитывают траектории движения космических кораблей и решают множество технических проблем. Наряду с другими функциями тригонометрические занимают важное место. Тригонометрия возникла из практических нужд человека. Современный вид тригонометрии придал крупнейший математик 18 столетия Леонард Эйлер. Почему летом жарко? Многие считают, что летом жарче, так как Земля находится ближе всего к солнцу, но это не так. Орбита Земля – это почти круг, в центре которого находится солнце, и расстояние от Земли меняется незначительно из месяца в месяц. Всё дело в наклоне земной оси по отношению к плоскости земной орбиты. Зимой солнце невысоко поднимается над горизонтом, его лучи лишь скользят по земле. Летом солнце приближается к зениту, лучи его падают почти отвесно. Поток солнечной энергии одинаков во все времена. Он зависит от угла падения лучей. Меняется угол падения и меняется доля солнечной энергии. Зависимость солнечной энергии от угла падения лучей и выражает график y = sinx.

В настоящее время изучению тригонометрических функций именно как функций числового аргумента уделяется большое внимание в школьном курсе алгебры за 10 класс. Тригонометрические функции представляют собой наиболее удобное и наглядное средство для изучения всех свойств функций (до применения производной), а в особенности такого свойства многих природных процессов как периодичность. Поэтому их изучению следует уделить пристальное внимание. Все выше сказанное и обуславливает актуальность выбора темы для данной работы.

1. Определение синуса и косинуса

Синус , одна из тригонометрических функций, обозначение sin. Синус острого угла в прямоугольном треугольнике называется отношение катета, лежащего против этого угла, к гипотенузе. Инд. математики синус обозначали словом «джива» (букв. — тетива лука). Арабы переделали этот термин в «джиба», который в дальнейшем превратился в «джайо» — обиходное слово арабского языка, означающее изгиб, пазуха, складка одежды, что соответствует латинскому слову sinus.

Косинус (новолат. cosinus, сокращение от complementi sinus — синус дополнения), одна из тригонометрических функций; обозначение cos. К. острого угла в прямоугольном треугольнике называется отношение катета, прилежащего к этому углу, к гипотенузе.

Т а нгенс (от лат. tangens — касающийся), одна из тригонометрических функций; обозначение tg. Т. острого угла в прямоугольном треугольнике называется отношение противолежащего катета к катету, прилежащему к этому углу.

Кот а нгенс (новолат. cotangens, сокращение от complementi tangens — тангенс дополнения), одна из тригонометрических функций , обозначение ctg. К. острого угла в прямоугольном треугольнике называется отношение катета, прилежащего к этому углу, к противолежащему катету.

Синусом α называется отношение AB/OB (отношение противолежащего катета к гипотенузе)

Косинусом α называется отношение ОА/OB (отношение прилежащего катета к гипотенузе)

Тангенсом α называется отношение AB/OA (отношение противолежащего катета к прилежащему)

Котангенсом α называется отношение ОА/AB (отношение прилежащего катета к противолежащему)

Секансом α называется отношение ОB/OA (отношение гипотенузы к прилежащему катету)

Косекансом α называется отношение ОB/AB (отношение гипотенузы к противолежащему катету)

3. Построение графиков с помощью упрощения уравнения функции. При построении графиков функций сложного вида можно примерно придерживаться следующего плана.

Найти область определения и область значений функции.

Выяснить, является ли функция четной (нечетной).

Выяснить, является ли функция периодической.

Найти точку пересечения графика функции с осью ординат.

Найти нули функции и промежутки знакопостоянства.

Вычислить производную функции f(x) и определить точки, в которых могут существовать экстремумы.

Найти промежутки монотонности функции.

Определить экстремумы функции.

Вычислить вторую производную f ( x )

Определить точки перегиба.

Найти промежутки выпуклости функции.

Найти асимптоты графика.

Найти значения функции в нескольких контрольных точках.

Построить эскиз графика функции.

a) Если sin x ˃ 0, то y=2 cos x │sin x│

Источник

Презентация на тему: «Построение тригонометрических функции»

Описание презентации по отдельным слайдам:

Тема: Тригонометрические функции y =sin x и y = cos x

III II I IY III IY I II p — шесть клеток О с ь С и н у с о в Построение графика функции y = sinx с применением тригонометрического круга y 0 1 -1 0

Устная разминка 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 ☺ cos90° sin90° sin(π/4) cos180° sin270° sin(π/3) cos(π/6) cos360° ctg(π/6) tg(π/4) sin(3π/2) cos(2π) cos(-π/2) cos(π/3) cos(‒π) 0 -1 1 1 -1 0 1 1/2 -1 1 -1 Молодец! √2/2 √3 √3/2 √3/2

Аналогично строится график функции y=cosx, он симметричен относительно оси OY. III IY I II III IY x 0 /6 /4 /3 /2 2/3 3/4 5/6  y=cos x 1 3/2 2/2 ½ 0 -½ -2/2 -3/2 -1

Свойства функции y = cos x Область определения: D(f): х  R; Множество значений: у  [-1;1]; Периодичность: Т = 2; Четность: четная, т.к. cos(-x) = cos x, график симметричен относительно оси ординат; Функция возрастает при: +2n  x  2(n+1), nZ; Функция убывает при: n  x   + 2n, n  Z.

Свойства функции y = cos x (продолжение) Функция принимает значения: Равные нулю при х=/2+n, nZ; Положительные при -/2+2n  x  /2+2n, nZ; Отрицательные при /2+2n  x  3/2+2n, nZ; Наибольшее, равное 1, при x = 2n, n  Z; Наименьшее, равное –1, при x =  + 2n, n  Z.

Свойства функции y = sin x Область определения: D(f): х  R; Множество значений: у  [-1;1]; Периодичность: Т = 2; Четность: НЕчетная, т.к. sin(-x) = — sinx, график симметричен относительно начала координат; Функция возрастает при: -/2+2k  x  /2+2k, kZ; Функция убывает при: /2+2k  x  3 /2 + 2 k, k  Z. x y

Свойства функции y = sin x (продолжение) Функция принимает значения: Равные нулю при х=k, kZ; Положительные при 2k  x  +2k, kZ; Отрицательные при +2k  x  2+2k, kZ; Наибольшее, равное 1, при x =  /2+2k, k  Z; Наименьшее, равное –1, при x = 3 /2+ 2k, k  Z. x y

Преобразование графиков тригонометрических функций. Построение графика функции у = sinx + m y= sin(x+t) y=f(kx) y=kf(x)

График функции y=f(x)+m получается параллельным переносом графика функции y=f(x) вдоль оси ОУ, вверх на m единиц, если m>0, или вниз, если m 11 слайд

График функции y = f(x + t) получается параллельным переносом графика функции y=f(x) вдоль оси ОХ на |t| единиц масштаба влево, если t > 0 и вправо, если t 12 слайд

Если известен график функции y=f(x), то график функции y=kf(x) строится посредством растяжения вдоль оси Оy исходного графика, пропорционально коэффициенту в k раз, а именно: — если m>0, то растяжение в k раз — если 0 13 слайд

Если известен график функции y=f(x), то график функции y=f(kx) строится посредством сжатия по оси Оx исходного графика пропорционально коэффициенту k при аргументе, а именно: — если k>1, то сжатие в k раз — если 0 14 слайд

I I I I I I I O x y -1 1 3cos x = y – Какие свойства еще изменились?

y x 1 -1 -1 Какие свойства еще изменились?

I I I I I I I O x y -1 1 Как найти период функции? cos 2x = y cos x = y 2π ІkІ Т= cos 4x = y

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 801 человек из 76 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 284 человека из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 605 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-720190

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Российский совет олимпиад школьников намерен усилить требования к олимпиадам

Время чтения: 2 минуты

Шойгу предложил включить географию в число вступительных экзаменов в вузы

Время чтения: 1 минута

Попова предложила изменить школьную программу по биологии

Время чтения: 1 минута

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

Российские школьники завоевали пять медалей на олимпиаде по физике

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник