Способы построения графиков 10 класс

1. Построение графиков функций

Теория:

Построение графиков любых функций выполняется по точкам. Однако не всегда заранее мы знаем как выглядит график. В этих случаях выделяют особо значимые точки графика, которые и задают его вид.

К особо значимым точкам графика функции y = f ( x ) относят:

— стационарные и критические точки;

— точки пересечения графика с осью \(x\) (нули функции) и с осью \(y\);

— точки разрыва функции.

Таким образом, для построения сложной функции сначала нужно исследовать свойства этой функции, найти важные её точки и уже потом по этим точкам строить график.

Существует чёткий план исследования свойств функции, позволяющий определить поведение функции на области определения и построить её график.

1) Когда функция y = f ( x ) непрерывна на всей числовой прямой, тогда определяют точки пересечения графика с осями координат, стационарные и критические точки, точки экстремума, промежутки монотонности и несколько контрольных точек, если это необходимо.

2) Когда функция y = f ( x ) определена не на всей числовой прямой, тогда в первую очередь находят область определения функции и точки разрыва.

3) Проверяют функцию на чётность, т. к. график чётной функции симметричен относительно оси \(y\) и график нечётной функций симметричен относительно начала координат. Значит, можно построить только ветвь графика при \(x>0\), а затем симметрично её отобразить.

4) Если lim x → ∞ f ( x ) = b , то, прямая \(y=b\) является горизонтальной асимптотой графика функции y = f ( x ) .

5) Прямая \(x=a\) является вертикальной асимптотой графика функции y = f ( x ) , если y → ∞ при x → a .

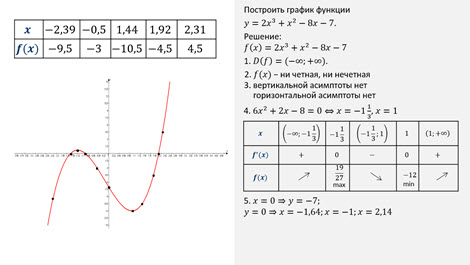
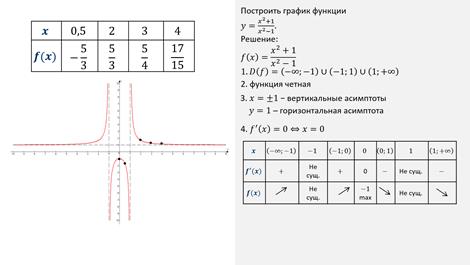
построить график функции y = x 2 + 4 x 2 − 4 .

Решение 1. Обозначим: f ( x ) = x 2 + 4 x 2 − 4 . Область определения этой функции: D ( f ) = ( − ∞ ; − 2 ) ∪ ( − 2 ; 2 ) ∪ ( 2 ; + ∞ ) , так как x ≠ 2, x ≠ − 2 .

2. Проведём исследование функции на чётность/нечётность:

f ( − x ) = − x 2 + 4 − x 2 − 4 = x 2 + 4 x 2 − 4 = f ( x ) .

Функция чётная. Следовательно, можно построить ветви графика функции для x ≥ 0 и отобразить их симметрично относительно оси ординат.

3. Определим асимптоты. Вертикальная асимптота: прямая \(x=1\), т. к. при \(x=1\) знаменатель дроби равен нулю, а числитель при этом не равен нулю. Для определения горизонтальной асимптоты вычисляем lim x → ∞ f ( x ) :

lim x → ∞ x 2 + 4 x 2 − 4 = lim x → ∞ x 2 x 2 + 4 x 2 x 2 x 2 − 4 x 2 = lim x → ∞ 1 + 4 x 2 1 − 4 x 2 = 1 .

Следовательно, \(y=1\) — горизонтальная асимптота.

4. Определим стационарные и критические точки, точки экстремума и промежутки монотонности функции:

y ′ = x 2 + 4 x 2 − 4 ′ = ( x 2 + 4 ) ′ ⋅ ( x 2 − 4 ) − ( x 2 + 4 ) ⋅ ( x 2 − 4 ) ′ x 2 − 4 2 = 2 x ⋅ ( x 2 − 4 ) − ( x 2 + 4 ) ⋅ 2 x x 2 − 4 2 = 2 x 3 − 8 x − 2 x 3 − 8 x x 2 − 4 2 = = − 16x x 2 − 4 2 .

Производная существует на всей области определения функции, следовательно, критических точек у функции нет.

Стационарные точки определим из уравнения y ′ = 0 . Получаем: \(-16x=0\) — откуда получаем, что \(x=0\). При \(x y ′ > 0 ; при \(x>0\) имеем: y ′ 0 . Таким образом, в точке \(x=0\) функция имеет максимум, причём y max = f ( 0 ) = 0 2 + 4 0 2 − 4 = − 1 .

При \(x>0\) имеем: y ′ 0 . Учитывая точку разрыва \(x=2\), делаем вывод: функция убывает на промежутках 0 ; 2 ) и ( 2 ; + ∞ ) .

5. Найдём несколько точек, принадлежащих графику функции f ( x ) = x 2 + 4 x 2 − 4 при x ≥ 0 :

Источник

Цикл уроков , алгебра 10 класс «Построение графиков функций»

Выберите документ из архива для просмотра:

Выбранный для просмотра документ построение графиков функции , урок 3.ppt

Описание презентации по отдельным слайдам:

Описание слайда:

Урок 3.
Тема: «Построение графика функции».

Учитель математики Жубанова Ботагуз Конлямжановна
2016-2017 учебный год

Описание слайда:

Найти ошибку. Проверка теоретического материала. Отвечать должны только да или нет.
1. Функция возрастает на [-7; 2) и (2; 8], значит, она возрастает на [-7; 8]. Верно ли?
2. Производная функции в точке х0 равна 0, значит х0 — критическая точка. Верно ли?
3. Производная функции не существует в точке х0, значит х0 — критическая точка. Верно ли?
4. Критическая точка является точкой экстремума. Верно ли?
5. Точка экстремума является критической точкой. Верно ли?

Описание слайда:

Описание слайда:

Построить график функции

Описание слайда:

Домашнее задание : №31.12(а), 31.13.

Описание слайда:

Описание слайда:

Описание слайда:

Выбранный для просмотра документ построение графиков функции . урок 1.doc

Предмет: алгебра и начала анализа, 10 класс

Автор: А.Г. Мордкович, 2012 год.

Уровень обучения базовый

Тема урока Построение графиков функций

Общее количество часов, отведенное на изучение темы- 34 часа

Место урока в системе уроков по теме – урок № 26, заключительный урок в теме;

Урок на тему: Построение графиков функций».

Тип урока: изучение нового материала.

¾ Продолжать учить работать с теоретическим материалом самостоятельно;

¾ обобщить и закрепить понятие геометрического смысла производной;

¾ развивать мышление, смысловую память, произвольное внимание учащихся,

¾ развивать навыки исследовательской деятельности

¾ формировать навыки самоконтроля при выполнении самостоятельной работы

¾ культуру математической речи;

¾ трудолюбие, аккуратность при выполнении любого задания;

¾ развивать у учащихся коммуникативные компетенции,

¾ формировать навыки взаимопомощи, взаимоконтроля.

¾ Карточки с заданиями для самостоятельной работы.

Тип урока: урок объяснения нового материала

1. Организационный момент

2. Актуализация знаний

3.Изучение нового материала

4. Закрепление изученного на практике

5. Постановка задания на дом

1. Организационный момент.

2. Проверка готовности класса к уроку. Сообщение темы и цели урока.

3. Устная фронтальная работа.

а )Повторение формул сложной функции.

б)

Для функции y = f(x) (график функции изображен на слайде ) найдите:

А) промежутки возрастания и убывания функции;

Б) точки максимума и минимума;

В) экстремумы функции;

Г) наибольшее и наименьшее значение на отрезках [-7;-4], [-4;0], [-7;7].

Сегодня на уроке мы обобщим и закрепим идею геометрического смысла производной, сформируем начальное представление о приложениях производной в математике и истории их развития, «откроем» зависимость между свойствами монотонности функции, экстремумами и значениями производной; рассмотрим план дальнейшего изучения темы «Исследование свойств функций при помощи производной.

Дома Вы должны были выполнить лабораторную работу: по предложенному графику функции схематично по точкам построить график её производной, используя геометрический смысл производной. А также Вы должны были ответить на вопросы. Проверим, как вы справились с домашним заданием.

• Назовите промежутки убывания функции (кадр).
• Отметим эти промежутки на графике производной функции (кадр).
• В каждой точке промежутков убывания проведем касательные (кадр). Под каким углом наклонена касательная к положительному направлению оси ОХ?
• Какой знак имеет производная?
• Отметим знаки значений производной на графике производной (кадр).
• Назовите промежутки возрастания функции (кадр).
• Отметим эти промежутки на графике функции (кадр).
• В каждой точке промежутков возрастания проведем касательные (кадр). Под каким углом наклонена касательная к положительному направлению оси ОХ?
• Какие значения имеет производная?
• Отметим знаки значений производной и её нулевые значения на графике производной (кадр).
• Назовите точки экстремумов функции.
• Отметим эти точки на графике функции (кадр).
• Проведем касательные в каждой точке экстремума (кадр).
• В каждой ли точке экстремума можно провести касательную? Если можно, то какой угол она образует с положительным направлением оси ОХ?
• В каждой ли точке экстремума существует значение производной? Если такое значение существует, то чему оно равно?

Постановка проблемы и выдвижение гипотезы.

Учащиеся проводят обсуждение ответов, выдвигают идеи по дальнейшему плану действий по исследованию функции. Какие точки являются важными при исследовании и построении графика функции.

Работа с учебником. П31 стр 188.

Учитель подводит итог.

Итак, особо важные точки:

Стационарные и критические, точки экстремума,

Точки пересечения с осями координат, точки разрыва функций.

Проверка уровня знаний и умений по теме «Связь свойств функции и производной» в форме тестирования.

На рисунке изображён график производной некоторой функции. Укажите в таблице интервалы, на которых функция обладает указанным свойством:

Источник

Построение графиков функций

Урок 46. Алгебра 10 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Построение графиков функций»

· рассмотреть применение производных для построения графиков.

Прежде чем приступить к изучению нового материала, выполните упражнение.

Мы с вами уже построили достаточно много графиков функции. Для того, чтобы построить графики функции мы с вами строили таблицу значений функций, отмечали точки с полученными координатами на плоскости и соединяли плавно полученные точки. Как же мы выбирали точки для построения таблиц? А выбирали мы их произвольно.

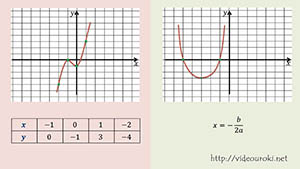
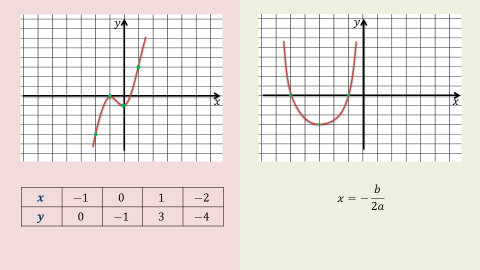
Но иногда, например, когда речь шла о параболе, мы находили координаты именно вершины параболы или искали точки пересечения графика функции с осями. Но если дальше продолжать строить по произвольным точкам, то может получиться так, что свойства функции не будут видны на графике. Пусть у нас есть таблица значений для некой функции f(x). Давайте отметим их на координатной плоскости и плавно соединим. Получим график функции f(x). А теперь давайте посмотрим, как выглядел бы график нашей функции, если бы мы не включили в таблицу эту точку? Тогда бы вид графика был совершенно другой. И мы бы не могли по графику сказать существуют ли экстремумы функции.

Чтобы такого не происходило надо выбирать особо важные точки графика, которые определяют его вид.

К особо важным точкам графика функции f(x) относят:

– стационарные и критические точки;

– точки пересечения графика функции с осями координат;

– точки разрыва функции.

В курсе математического анализа разработана универсальная схема исследования свойств функции и построения её графика. Мы будем использовать упрощённые варианты указанной схемы.

Давайте рассмотрим несколько примеров.

Рассмотрим ещё один пример.

Давайте ещё раз повторим схему исследования функции для построения её графика.

Источник

Конспект урока по алгебре и началам анализа на тему «Построение графиков функций» (10 класс)

Предмет: алгебра и начала анализа

Класс: 10 класс по программе Мордковича А.Г.

Тема: Построение графиков функций.

Систематизировать знания, умения учащихся при построении графиков функций.

Развитие творческих способностей и логического мышления.

Мотивация учения школьников, сообщение темы, целей урока.

Математический диктант по теории.

Итог урока. Домашнее задание.

листы с теоретическими заданиями для математического диктанта;

бланки ответов с копировально бумагой;

изображение графика тригонометрической функции для проведения устного исследования по нему;

сообщения учащихся к уроку и приложения к ним.

Девиз: В математике исследует помнить не формулы,

а процессы мышления.

Мотивация учения школьников, сообщение темы и целей.

Учитель: назовите этапы очередности при исследовании функции?

Область определения и область значения функции

Вид функции (четная, нечетная, периодическая)

Точки пересечения с осями координат

Промежутки возрастания и убывания функции, экстремумы.

Установить истинны или ложны данные высказывания?

Ответы записывать на двойных листах с копировальной бумагой, по оканчании работы верхний лист ответов и копировальную бумагу передать мне, а нижний лист оставить себе для проверки.

Областью определения функции являются все значения переменной х.

Если выполняется f (- x )= f (х), то функция нечетная

Наименьший период функции y = tg x равен 2П

Если f `(х)  0, то функция убывает

Если в точке производная меняет знак с «+» на «-», то эта точка – точка максимума

Областью значения функции является все значения переменной у.

Если выполняется f (- x )= — f (х), то функция нечетная

Наименьший период функции у= sin x равен 2П

Если f (х)  0, о функция убывает.

Если в точке производная меняет знак с «-» на «+», то это точка – точка максимума

Проводится публичное выяснение результатов проведенного диктанта. Кто получил «5»?, Кто получил «4»?

Провести исследование функции у = 3 cos (1,5х – 60) по графику.

1) как построить график данной функции с помощью преобразований?

сжатие к оси ординат в 1,5 раза

параллельный перенос на вектор ( ;0)

растяжение от оси абсцисс в 3 раза

у = 3 cos (1,5х – 60)

2) Исследовать функцию у = ¼ х 4 – 3/2 х 2 по общей схеме исследования:

1) Областью определения функции является множество действительных чисел D = R

2) Определим вид функции:

— Область определения функции симметрична относительно нуля;

— f (- x )= f (х) =  четная

3) Найдем точки пересечения графика с осями координат:

С осью абсцисс: 1/4х 4 -3/2 х 2 =0

х ₁ = 0 или 1/4х2 = 3/2

(0,0); (  6; 0); (-  6 ;0) координаты точек пересечения графика с осями координат.

4) асимптот нет, так как нет точек разрыва.

5) Исследуем функцию на монотонность и экстремумы:

у` = х 3 – 3х = х(х 2 -3)

— + — + y`

т .min т .max т .min

у(  3) = у(-  3) = 1/4 *9-3/2 *3 = 9/4-9/2 = -2,25

6)у « = 3х 2 – 3 = 3 (х 2 -1)

х =  1 – точки перегиба

+ — + у «

у(-1) = у(1) = 1/4 -3/2 = -7/4 = 1,75

3) Другие способы построения графиков (сообщения учащихся):

А) Умножение и деление графиков.

Пусть требуется построить график функции у = f (х) g (х).

Для построения графика надо построить график функции f (х) и g (х) и перемножить значения ординат, соответствующие одним и тем же значениям аргумента.

Деление графиков можно привести к умножению.

Иногда произведение или частное двух функций можно упростить, и построение графика значительно облегчается.

Построим график функции у = х sin x . Для этого строим графики функций f (х) = х и f (х) = sin x . График функции у получаем перемножением значений ординат этих графиков, соответствующих одной и той же абсциссе х. Построение можно производить только при х  0, а затем отразить полученный график относительно оси ординат, так как функция у является четной. График заключен между прямыми у = х и у = -х,

причем в точках х =  , в которых sin = —  /2 + 2  , где sin х = 1, у = х,

а в точках х = —  /2 + 2  , где sin х = -1, у = 1

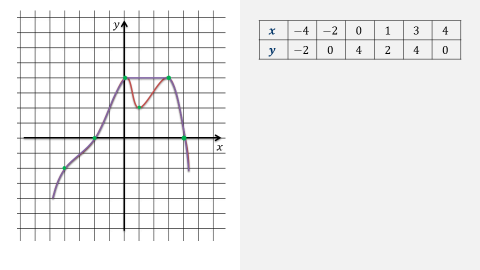
На рис изображен график функции у = f (х).

В)Учащиеся 10- класса хорошо знают, как строить графики простейших функций y = ax 2 + bx + c , y = ax n , e = k / x , y = kx + b ,

и помнят основные преобразования графиков. Сначала продемонстрируем суть метода. Исследуем функцию f (х) = 4х 2 – х 4 и построим ее график. Представим f (х) в виде суммы 4х 2 и –х 4 . какое слагаемое вблизи нуля играет большую роль?

Модуль какого слагаемого больше при очень малых х? Сообща приходим к «открытию»: вблизи нуля график функции f (х) = 4х 2 – х 4 похож на у = 4х 2 (второе гораздо меньше по модулю слагаемое, мы «отбросили»).

Как же будет вести себя функция на бесконечности, т.е. при очень больших по модулю х? В этом случае, «отбросив» незначительное уже первое слагаемое, получаем, что на бесконечности функция f (х) ведет себя как у = — х 4 . Рисуем эскиз на доске и в тетрадях, плавно соединяя «куски» графика и учитывая четность функции .

Решив уравнение 4х 2 – х 4 = 0, найдем точки пересечения графика с осью абсцисс: х = 0, х = 2, х = — 2. Используя метод интервалов убедимся, что при переходе через точку х = 0 знак функции не изменится, а через точки х = 2 и х = — 2 изменяется.

Точки экстремума целесообразнее найти, выделив полный квадрат:

— х 4 + 4х 2 = — (х 4 -4х 2 + 4) + 4 = — (х2 — 2)2 + 4.

Отсюда видно, что наибольшее значение функции 4 достигается в двух точках:  2 и —  2.

Источник