AutoCAD
Автор:
Построение эллипсов и эллиптических дуг.
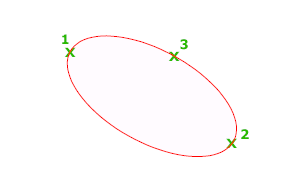
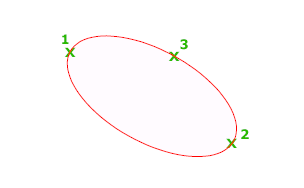
Первые две точки эллипса определяют местоположение и длину первой оси. Третья точка определяет расстояние между центром эллипса и конечной точкой второй оси.
Отображаются следующие запросы.
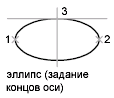
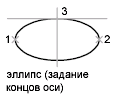
Конечная точка оси
Задание первой оси по двум точкам. Угол поворота первой оси задает поворот всего эллипса. Первой может строиться как большая, так и малая ось эллипса.
Длина второй оси отсчитывается от середины первой оси до конечной точки (3) второй оси.
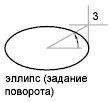
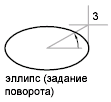
Построение эллипса путем поворота круга относительно первой оси.
Перемещайте перекрестье вокруг центра и нажмите кнопку мыши для построения эллипса. Чем больше угол поворота, тем выше эксцентриситет эллипса. Если угол равен 0, строится круг.
Построение эллиптической дуги.
Угол поворота первой оси задает поворот всей эллиптической дуги. Первой может строиться как большая, так и малая ось эллипса, в зависимости от ее размера.
Первые две точки эллиптической дуги определяют местоположение и длину первой оси. Третья точка определяет расстояние между центром эллиптической дуги и конечной точкой второй оси. Четвертая и пятая точки определяют начальный и конечный углы.
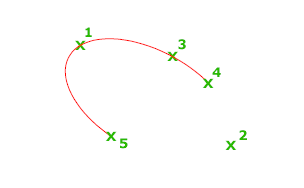
Задание начала первой оси.
Отношение длин осей эллипса задается путем поворота круга относительно первой оси. Чем больше угол поворота (его величина должна находиться в диапазоне от 0 до 89,4 градусов), тем больше отношение малой оси к большой. Углы поворота со значениями от 89,4 до 90,6 градусов являются недопустимыми, поскольку эллипс в этом случае будет выглядеть как прямая линия. Значения, кратные этим значениям угла поворота, приводят к зеркальному эффекту через каждые 90 градусов.
Задание первой конечной точки эллиптической дуги. Параметр «Начальный угол» служит также для изменения режима «Параметр» на режим «Угол». Режим контролирует вычисления эллипса.
Параметр (специализированный параметр)
Требуется указать углы. Эллиптическая дуга создается с помощью следующего параметрического векторного уравнения для угла каждой конечной точки:
p(угол) = c + a * cos(угол) + b * sin(угол)
, где c является центром эллипса, a и b — это отрицательные длины его большой и малой осей.
- Конечный параметр: задание конечного угла эллиптической дуги с использованием векторного параметрического уравнения. Опция «Начальный параметр» служит для переключения между режимами «Угол» и «Параметр». Режим контролирует вычисления эллипса.
- Угол: задание конечного угла эллиптической дуги. Опция «Угол» служит для переключения между режимами «Параметр» и «Угол». Режим контролирует вычисления эллипса.
- Внутренний угол: задание внутреннего угла эллиптической дуги; отмеряется относительно начального угла.
Центр
Создание эллипса с помощью центральной точки, конечной точки первой оси и длины второй оси. Можно задать расстояния, щелкнув в точке на требуемом расстоянии или с помощью ввода значения длины.
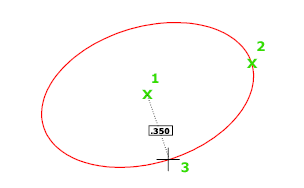
Длина второй оси отсчитывается от середины первой оси до указанной точки.
Построение эллипса путем поворота круга относительно первой оси.
Перемещайте перекрестье вокруг центра и нажмите кнопку мыши для построения эллипса. Чем больше угол поворота, тем выше эксцентриситет эллипса. Если угол равен 0, строится окружность.
Изокруг
Построение окружности в текущей плоскости изометрии.
Построение окружности с указанным радиусом.
Построение окружности с указанным диаметром.
Источник
Эллипс в Автокаде
| Команда рисования в AutoCAD | |
| Эллипс | |
 | |
| Определение | |
| Эллипс в Автокаде — это геометрическая фигура, которая по умолчанию определяется двумя осями (большая и малая ось эллипса). Примечание: Программа определяет, какая ось является большой, а какая — малой, основываясь на их относительной длине. Если задать равную длину осей эллипса, получится окружность, представляющая собой объект эллипс в Автокад. | |
| Инструмент | |
| Инструмент Эллипс — команда, позволяющая строить эллипсы и эллиптические дуги. Первые две точки эллипса определяют местоположение и длину первой оси. Третья точка определяет расстояние между центром эллипса и конечной точкой второй оси. | |
| Команда | |
| Эллипс | |
| Объект | |
| Эллипс |
В двухмерном проектировании объект Эллипс в AutoCAD используется довольно редко, но довольно часто в изометрическом проектировании. Команда Эллипс позволяет строить круги в аксонометрии, так как имеет в своем функционале инструмент Изокруг.
Команда AutoCAD Эллипс (Ellipse)
За создание эллипса в Автокад отвечает команда Эллипс/Ellipse, вызвать которую можно следующими способами (начать его построение):
- построить эллипсы в Автокаде можно из строки меню пункт Рисование — строка Ellipse;
- создать его можно из вкладки Главная ленты инструментов — в группе инструментов Рисование кнопка «Центр, (Ось, конец)», т.е. вам сразу в ленте доступны опции команды Эллипс в Автокаде;
- нарисовать объект Эллипс можно из классической панели инструментов Рисование кнопка Ellipse;
- а так же непосредственное создание эллипса в программе из командной строки, прописав наименование команды в командной строке Эллипс/Ellipse.
Источник
AutoCAD
Автор:
Построение эллипсов и эллиптических дуг.
Первые две точки эллипса определяют местоположение и длину первой оси. Третья точка определяет расстояние между центром эллипса и конечной точкой второй оси.
Отображаются следующие запросы.
Конечная точка оси
Задание первой оси по двум точкам. Угол поворота первой оси задает поворот всего эллипса. Первой может строиться как большая, так и малая ось эллипса.
Длина второй оси отсчитывается от середины первой оси до конечной точки (3) второй оси.
Построение эллипса путем поворота круга относительно первой оси.
Перемещайте перекрестье вокруг центра и нажмите кнопку мыши для построения эллипса. Чем больше угол поворота, тем выше эксцентриситет эллипса. Если угол равен 0, строится круг.
Построение эллиптической дуги.
Угол поворота первой оси задает поворот всей эллиптической дуги. Первой может строиться как большая, так и малая ось эллипса, в зависимости от ее размера.
Первые две точки эллиптической дуги определяют местоположение и длину первой оси. Третья точка определяет расстояние между центром эллиптической дуги и конечной точкой второй оси. Четвертая и пятая точки определяют начальный и конечный углы.
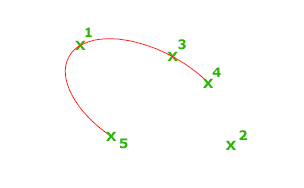
Задание начала первой оси.
Отношение длин осей эллипса задается путем поворота круга относительно первой оси. Чем больше угол поворота (его величина должна находиться в диапазоне от 0 до 89,4 градусов), тем больше отношение малой оси к большой. Углы поворота со значениями от 89,4 до 90,6 градусов являются недопустимыми, поскольку эллипс в этом случае будет выглядеть как прямая линия. Значения, кратные этим значениям угла поворота, приводят к зеркальному эффекту через каждые 90 градусов.
Задание первой конечной точки эллиптической дуги. Параметр «Начальный угол» служит также для изменения режима «Параметр» на режим «Угол». Режим контролирует вычисления эллипса.
Параметр (специализированный параметр)
Требуется указать углы. Эллиптическая дуга создается с помощью следующего параметрического векторного уравнения для угла каждой конечной точки:
p(угол) = c + a * cos(угол) + b * sin(угол)
, где c является центром эллипса, a и b — это отрицательные длины его большой и малой осей.
- Конечный параметр: задание конечного угла эллиптической дуги с использованием векторного параметрического уравнения. Опция «Начальный параметр» служит для переключения между режимами «Угол» и «Параметр». Режим контролирует вычисления эллипса.
- Угол: задание конечного угла эллиптической дуги. Опция «Угол» служит для переключения между режимами «Параметр» и «Угол». Режим контролирует вычисления эллипса.
- Внутренний угол: задание внутреннего угла эллиптической дуги; отмеряется относительно начального угла.
Центр
Создание эллипса с помощью центральной точки, конечной точки первой оси и длины второй оси. Можно задать расстояния, щелкнув в точке на требуемом расстоянии или с помощью ввода значения длины.
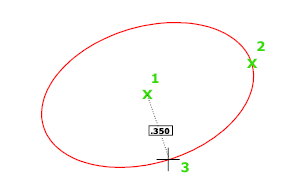
Длина второй оси отсчитывается от середины первой оси до указанной точки.
Построение эллипса путем поворота круга относительно первой оси.
Перемещайте перекрестье вокруг центра и нажмите кнопку мыши для построения эллипса. Чем больше угол поворота, тем выше эксцентриситет эллипса. Если угол равен 0, строится окружность.
Изокруг
Построение окружности в текущей плоскости изометрии.
Создание изометрического представления окружности с использованием заданного значения радиуса.
Создание изометрического представления окружности с использованием заданного значения диаметра.
Источник
AutoCAD
Не удалось извлечь оглавление
ЭЛЛИПС (команда)
Автор:
Построение эллипсов и эллиптических дуг.
Первые две точки эллипса определяют местоположение и длину первой оси. Третья точка определяет расстояние между центром эллипса и конечной точкой второй оси.
Отображаются следующие запросы.
Конечная точка оси
Задание первой оси по двум точкам. Угол поворота первой оси задает поворот всего эллипса. Первой может строиться как большая, так и малая ось эллипса.
Длина второй оси отсчитывается от середины первой оси до конечной точки (3) второй оси.
Построение эллипса путем поворота круга относительно первой оси.
Перемещайте перекрестье вокруг центра и нажмите кнопку мыши для построения эллипса. Чем больше угол поворота, тем выше эксцентриситет эллипса. Если угол равен 0, строится круг.
Построение эллиптической дуги.
Угол поворота первой оси задает поворот всей эллиптической дуги. Первой может строиться как большая, так и малая ось эллипса, в зависимости от ее размера.
Первые две точки эллиптической дуги определяют местоположение и длину первой оси. Третья точка определяет расстояние между центром эллиптической дуги и конечной точкой второй оси. Четвертая и пятая точки определяют начальный и конечный углы.
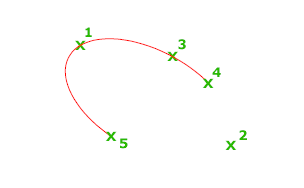
Задание начала первой оси.
Отношение длин осей эллипса задается путем поворота круга относительно первой оси. Чем больше угол поворота (его величина должна находиться в диапазоне от 0 до 89,4 градусов), тем больше отношение малой оси к большой. Углы поворота со значениями от 89,4 до 90,6 градусов являются недопустимыми, поскольку эллипс в этом случае будет выглядеть как прямая линия. Значения, кратные этим значениям угла поворота, приводят к зеркальному эффекту через каждые 90 градусов.
Задание первой конечной точки эллиптической дуги. Параметр «Начальный угол» служит также для изменения режима «Параметр» на режим «Угол». Режим контролирует вычисления эллипса.
Параметр (специализированный параметр)
Требуется указать углы. Эллиптическая дуга создается с помощью следующего параметрического векторного уравнения для угла каждой конечной точки:
p(угол) = c + a * cos(угол) + b * sin(угол)
, где c является центром эллипса, a и b — это отрицательные длины его большой и малой осей.
- Конечный параметр: задание конечного угла эллиптической дуги с использованием векторного параметрического уравнения. Опция «Начальный параметр» служит для переключения между режимами «Угол» и «Параметр». Режим контролирует вычисления эллипса.
- Угол: задание конечного угла эллиптической дуги. Опция «Угол» служит для переключения между режимами «Параметр» и «Угол». Режим контролирует вычисления эллипса.
- Внутренний угол: задание внутреннего угла эллиптической дуги; отмеряется относительно начального угла.
Центр
Создание эллипса с помощью центральной точки, конечной точки первой оси и длины второй оси. Можно задать расстояния, щелкнув в точке на требуемом расстоянии или с помощью ввода значения длины.
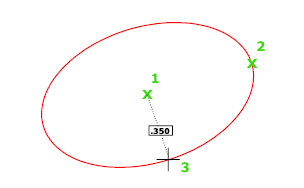
Длина второй оси отсчитывается от середины первой оси до указанной точки.
Построение эллипса путем поворота круга относительно первой оси.
Перемещайте перекрестье вокруг центра и нажмите кнопку мыши для построения эллипса. Чем больше угол поворота, тем выше эксцентриситет эллипса. Если угол равен 0, строится окружность.
Изокруг
Построение окружности в текущей плоскости изометрии.
Создание изометрического представления окружности с использованием заданного значения радиуса.
Создание изометрического представления окружности с использованием заданного значения диаметра.
Источник