Способы построения биссектрисы угла

Мы дали ответ на поставленный вопрос — как построить биссектрису данного угла.

Доказательство

Теперь, разобравшись, как построить биссектрису данного угла, стоит вспомнить еще одно определение биссектрисы, используя термин «геометрическое место точек». Биссектрисой называется геометрическое место точек, которые равноудалены от лучей, образующих угол.

Согласно выполненному построению в пунктах 4-6, точка, принадлежащая построенной биссектрисе, также принадлежит двум окружностям, равным по радиусу, центр которых располагается на лучах, образующих угол на одинаковом расстоянии от вершины угла (согласно пунктам 1-3 построения). Опустим перпендикуляр из отмеченной в пункте 6 точки на лучи, образующие угол. Докажем, что получившиеся прямоугольные треугольники равны, и выясним, что опущенные перпендикуляры также равны, как соответствующие элементы треугольников. Таким образом, их общая гипотенуза является биссектрисой угла по определению. Что и требовалось доказать.

Источник

Способы построения биссектрисы угла

ТЕМА УРОКА: Построение биссектрисы угла.

Содержание

Цели урока:

• Образовательные – повторение, обобщение и проверка знаний по теме: “Построение биссектрисы угла”; выработка основных навыков.
• Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
• Воспитательные — посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.

Задачи урока:

• Формировать навыки в построении биссектрисы с помощью масштабной линейки, транспортира и чертежного треугольника.
• Проверить умение учащихся решать задачи.

План урока:

• Определение угла.
• Определение развёрнутого угла.
• Понятия внутренней и внешней областей угла.
• Сравнение углов.
• Измерение углов.
• Виды углов.
• Измерение углов на местности.

3) Биссектриса угла.
4) Построение биссектрисы угла.
5) Примеры задач.

Из истории.

Самой древней математической деятельностью был счет. Счет был необходим, чтобы следить за поголовьем скота и вести торговлю. Некоторые первобытные племена подсчитывали количество предметов, сопоставляя им различные части тела, главным образом пальцы рук и ног. Наскальный рисунок, сохранившийся до наших времен от каменного века, изображает число 35 в виде серии выстроенных в ряд 35 палочек-пальцев. Первыми существенными успехами в арифметике стали концептуализация числа и изобретение четырех основных действий: сложения, вычитания, умножения и деления. Первые достижения геометрии связаны с такими простыми понятиями, как прямая и окружность. Дальнейшее развитие математики началось примерно в 3000 до н.э. благодаря вавилонянам и египтянам.

Использование руки для счета («на пальцах») и физиология руки сделали возможным древний метод рассчитывания лунных фаз и календарных дат по руке (счет велся в основном по фалангам пальцев). Так, в Древней Руси календарные и пасхальные таблицы рассчитывались «по руке». «Руки», т.е. различные способы счисления по руке носили особые названия, например: «рука рождению или ущерблению Луны», «о часах боевых како их учитать по руце», «рука Иоанна Дамаскина — круг Солнца»

Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а их общее начало – вершиной угла.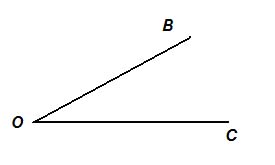

∠ВОС – угол с вершиной в точке О и со сторонами ОВ и ОС.

Определение развёрнутого угла.

Угол называется развёрнутым, если обе его стороны kежат на одной прямой. Можно сказать, что каждая сторона развёрнутого угла является продолжением другой стороны.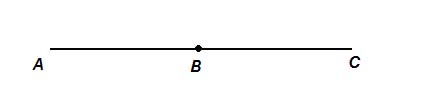

∠АВС – развёрнутый угол с вершиной в точке В и со сторонами ВА и ВС.

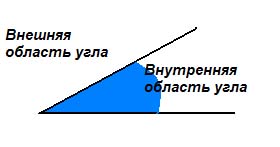
Понятия внутренней и внешней областей угла.

Любой угол разделяет плоскость на 2 части. Если угол неразвёрнутый, то одна из частей называется внутренней, а другая внешней областью этого угла.
Если угол развёрнутый, то любую из двух частей, на которые она разделяет плоскость можно считать внутренней областью угла.
Фигуру, состоящую из угла и его внутренней области, так же называют углом.

Если луч исходит из вершины неразвёрнутого угла и проходит внутри угла, то он делит этот угол на два угла.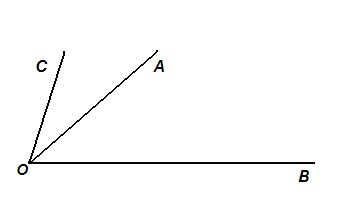

∠СОВ разделен лучом ОА на два угла ∠СОА и ∠ВОА.

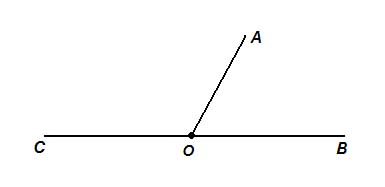
Чтобы установить, равны углы или нет, нужно наложить один из них на другой так, чтобы сторона одного угла совместилась со стороной другого, а две другие оказались по одну сторону от совместившихся сторон.

Если две другие стороны совместятся, то углы полностью совместятся и, значит, они равны. Если же эти стороны не совместятся, то меньшим считается тот угол, который составляет часть другого.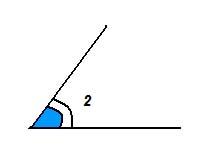

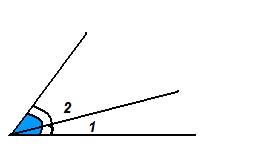
На рисунке угол 1 составляет часть угла 2, ∠1 Биссектриса угла.

Биссектриса (от лат. bi- «двойное», и sectio «разрезание») угла — луч с началом в вершине угла, делящий угол на две равные части.

Биссектриса угла (вместе с её продолжением) есть геометрическое место точек, равноудалённых от сторон угла (или их продолжений).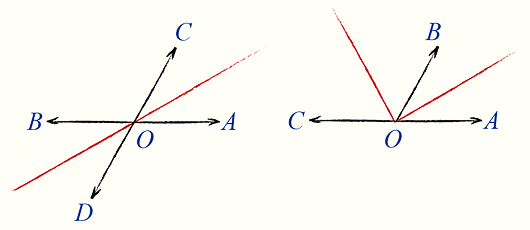

Толковый словарь русского языка под ред. Д. Н. Ушакова

БИССЕКТРИСА (от латин. bissectrix — секущая поперек).

1. В угле — прямая линия, делящая угол пополам.
2. В треугольнике — прямая линия, проведенная от какого-н. угла к противоположной стороне и делящая эту сторону на части, прямо пропорциональные двум другим сторонам.

Файл:T.gif Теорема о биссектрисе: Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон.

Файл:T.gif Теорема Штейнера — Лемуса. Если 2 биссектрисы равны, то треугольник — равнобедренный.

• Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам
• Биссектрисы внутренних углов треугольника пересекаются в одной точке — инцентре — центре вписанной в этот треугольник окружности.
• Если биссектриса внешнего угла треугольника пересекает продолжение противолежащей стороны, то AD/BD=AC/BC.
• Биссектрисы внутреннего и внешнего углов перпендикулярны.
• Биссектрисы одного внутреннего и двух внешних углов треугольника пересекаются в одной точке. Эта точка — центр одной из трёх вневписанных окружностей этого треугольника.
• Основания биссектрис двух внутренних и одного внешнего углов треугольника лежат на одной прямой, если биссектриса внешнего угла не параллельна противоположной стороне треугольника.
• Построение треугольника по трем заданным биссектрисам с помощью циркуля и линейки невозможно, причём даже при наличии трисектора

Построение биссектрисы угла.

Построить биссектрису данного угла.

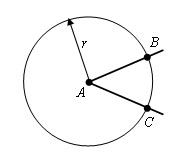
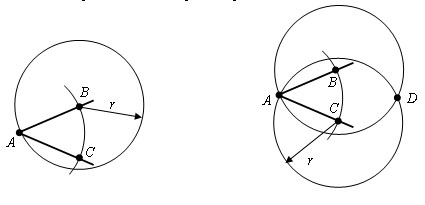
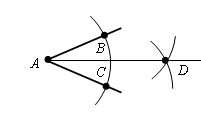
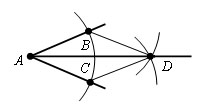
Из вершины A данного угла как из центра описываем окружность произвольного радиуса r. Пусть B и С – точки ее пересечения со сторонами угла.

Из точек В и С проведем окружности тем же радиусом r. Пусть точка D – точка их пересечения отличная от A.

Проведем луч AD.

Проведем отрезки BD и CD. Δ ABD = Δ ACD, по третьему признаку равенства треугольников. Отсюда ∠ BAD = ∠ CAD и следовательно AD – биссектриса угла BAC.

Примеры задач.

Построить биссектрису данного угла.

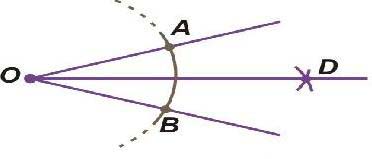
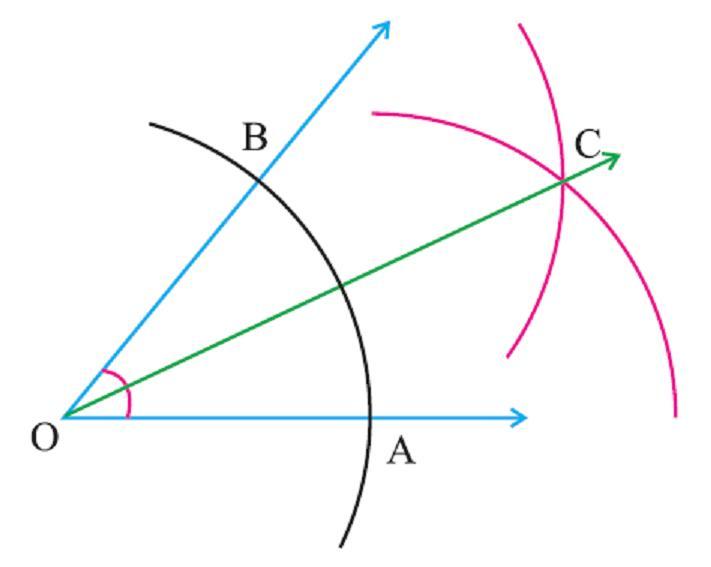
Решение. Пусть дан угол АОВ. Приложив один конец циркуля к точке О, т.е. за центр возьмем точку О, произвольным раствором циркуля проведем дугу. Пусть А и В – точки пересечения дуги с лучами ОА и ОВ. Теперь из точек А и В, раствором циркуля, равным АВ, проведем две дуги. Если D точка пресечения будет во внутренней области, то проведем луч OD. Этот луч является биссектрисой угла АОВ, так как, ∆АОD=∆DОВ.
Замечание. Проведя биссектрису, мы говорим, что «данный угол поделили на два равных угла». Вышесказанным способом также каждую часть можно поделить на две части. И тогда, данный угол поделится на четыре равных угла и т.д. Но произвольный угол нельзя поделить, с помощью циркуля и линейки, на три равных угла (в истории математики эта задача получила название задача о трисекции угла).

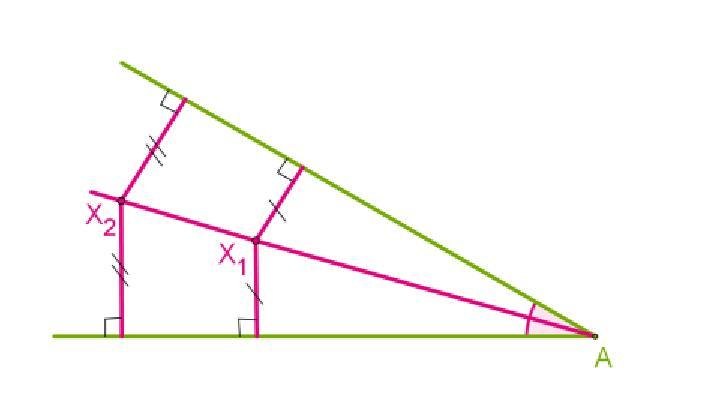
Условие. Через вершины А и С треугольника АВС проведены прямые, перпендикулярные биссектрисе угла АВС. Они пересекают прямые СВ и ВА в точках К и М соответственно. Найдите длину АВ, если ВМ = 8 см, KC = 1 см и АВ > ВС.

Решение. В треугольниках ABK и MBC биссектрисы одновременно являются и высотами (см. рис.), поэтому эти треугольники — равнобедренные. Так как АВ > ВС, то точка M лежит на стороне АВ, а точка K — продолжении стороны ВС. Значит, BC = BM = 8 (см); AB = BK = BC + CK = 9 (см).

Задание для самостоятельной проверки.

1 вариант: Построить биссектрису остроугольного треугольника.
2 вариант: Построить биссектрису тупоугольного треугольника.
3 вариант: Построить биссектрису прямоугольного треугольника.

Вплоть до XIX в. никто не сомневался ни в истинности пятого постулата, ни в том, что евклидова геометрия единственно возможна, ни в том, что она описывает реальный физический мир.

Конечно, великолепной была его попытка дать аксиоматическое изложение геометрии, т.е. сформулировать небольшое количество простых предложений (аксиом), из которых логически выводятся все теоремы геометрии. Но предложенный Евклидом список аксиом вскоре подвергся критике. Например, одна из них, утверждавшая, что «все прямые углы равны между собой», оказалась просто ненужной. Ее удалось доказать с помощью остальных евклидовых аксиом.

Но одна из них — пятый постулат Евклида — вызывала особенные нарекания математиков. Именно эта аксиома, как показало историческое развитие науки, содержала в себе зародыш другой, неевклидовой геометрии.

Вот о чем говорится в пятом постулате:

Если две прямые а и в образуют при пересечении с третьей прямой внутренние односторонние углы a и в, сумма величин которых меньше двух прямых углов (т.е. меньше 180°), то эти две прямые обязательно пересекаются, причем именно с той стороны от третьей прямой, по которую расположены углы а и в (составляющие вместе менее 180°).

1. Что такое биссектриса?
2. Как она делит угол?
3. Что такое медиана?
4. Что такое высота?

Список использованных источников:

1. Урок на тему «Треугольники», Левченко В.С.
2. Журнал «Прикладная геометрия».
3. Урок на тему «Биссектриса» Автор: Крыжов В.А., г. Кривой Рог
4. Урок на тему «Углы» Автор: Марина Александровна, г. Киев

Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.

Источник