Способы построения картографических проекций
Картографические проекции
С тех пор ученые создали много различных способов приближенного изображения поверхности земного шара на картах, или картографических проекций, в основе которых лежат разные способы построения географической сетки.
Рассматривая глобус, не трудно убедиться, что все меридианы представляют собой большие (на глобусе они все одинаковой длины) окружности, пересекающиеся между собой только в двух точках — полюсах. Зато каждый меридиан пересекает все параллели, т. е. окружности, проведенные к ним под прямым углом. Самая длинная из окружностей-параллелей — это экватор, все точки которого отстоят от полюсов на равных расстояниях. С приближением к полюсам длина параллелей уменьшается, в пределе, сливаясь в одну точку. На картах же, в зависимости от выбранной проекции, меридианы и параллели изображаются то прямыми, а то различными кривыми линиями. Выбор проекции зависит от назначения карты. Например, для составления политической карты Европы более подходит такая проекция, которая дает правильное представление о размерах территории государств, позволяет сравнивать их площади. Проекции, при которых все площади одинаково уменьшаются, т. е. их отношения не искажаются, называются равновеликими. Напротив, для целей навигации (вождения кораблей и самолетов) нужны карты в равноугольных проекциях, на которых углы между различными направлениями на земной поверхности изображаются в натуральную величину, хотя при этом не сохраняются соотношения площадей.
Способы построения картографических проекций
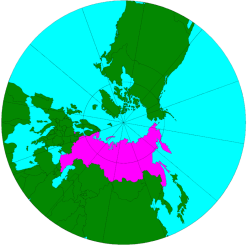
Схема построения азимутальной экваториальной проекции и карта Восточного полушария в этой же проекции.
Схема построения азимутальной полярной проекции и карта Антарктиды в этой же проекции.
Схема построения цилиндрической проекции. Жирная линия —’линия касания шара цилиндром. Справа — карта Восточного полушария в меркаторской проекции.
Положение глобуса и секущего цилиндра, на котором строится проекция М. Д. Соловьева. Жирная линия показывает линию пересечения шара цилиндром. По этой линии сохраняется точный масштаб. Справа — карта СССР в проекции М. Д. Соловьева.
Схема конической проекции на секущем конусе. Жирными линиями обозначены параллели сечения шара конусом. На этих параллелях сохраняется точный масштаб. Справа — карта СССР в конической равнопромежуточной проекции В. В. Каврайского.
Чтобы яснее представить себе приемы построения равноугольной проекции, вообразим, что мы взяли глобус, сделанный из прозрачного материала, и экран из прозрачной бумаги прислонили к одной из точек экватора. Если теперь осветить с другой стороны глобус лампой, расположенной на уровне экватора, на экран будет падать тень от изображенных на глобусе меридианов и параллелей, а также от очертаний континентов, морей и т. п. Обведя спроектированное на плоскую поверхность экрана изображение, мы получим карту в так называемой азимутальной экваториальной проекции, которая обычно применяется для изображения полушарий.
Если приложить экран к точке полюса глобуса, а лампу держать против другого полюса, то спроектируется карта в азимутальной полярной проекции. Она дает представление о приполярных областях.
Если же надеть на глобус цилиндр из прозрачной бумаги так, чтобы он касался линии экватора, а лампочку поместить внутри глобуса, на поверхности цилиндра получим изображение в цилиндрической проекции. .
Развернув поверхность цилиндра, мы увидим, что меридианы и параллели превратились в пересекающиеся под прямыми углами параллельные линии. В этой проекции искажения увеличиваются по мере удаления от экватора к полюсам, и ее следует применять для изображения стран, расположенных вблизи экватора.
Особенно велики искажения расстояний и площадей на цилиндрической проекции голландского картографа Меркатора. В полярных странах они так преувеличены, что площадь изображения Гренландии больше, чем всей Южной Америки, которая превосходит ее в действительности в восемь раз, а расстояние от Кольского полуострова до Чукотки кажется таким же, как от Кубы до Цейлона, хотя второе в два раза больше. Зато на этой карте легко определять нужное направление, т. е. углы-румбы, а это крайне важно в мореплавании и в авиации.
Чтобы проложить на карте путь корабля или самолета, штурман должен точно определить и направление движения, и протяженность каждого участка маршрута. Линия, пересекающая все меридианы под одним и тем же углом, называется локсодромией (по-гречески «локос» — косой, «дромос» — путь). На меркаторской карте она выглядит прямой линией: измерил угол транспортиром и держи курс по компасу. Но кратчайшее расстояние между двумя точками на сфере определяется по ортодромии (по-гречески «ортос» — прямой), которая пересекает меридианы под разными углами.
Широко распространены конические проекции, применяемые для изображения стран, лежащих в средних широтах и вытянутых с запада на восток, например для СССР. На картах в этой проекции меридианы изображаются прямыми линиями, расходящимися веером из одной точки, а параллели — дугами кругов с центром в той же точке полюса. Чтобы получить такую проекцию, наденем на наш прозрачный глобус бумажный конус так, чтобы он касался его по одной из параллелей. Если теперь осветить глобус с противоположной стороны и спроектировать его на поверхность конуса, а затем конус развернуть, то мы и получим карту в виде сектора. Точный масштаб на ней сохраняется по параллели, по которой конус касался глобуса; по мере удаления от нее искажения возрастают. Чтобы уменьшить эти искажения, используют не касательный, а секущий конус — тогда точный масштаб сохраняется по двум параллелям. Расчетом таких проекций занимаетсяматематическая картография.
Конечно, вид полушария, развернутого цилиндра или сектора имеет карта, на которой спроектирован весь земной шар. Обычно же на карте изображается лишь часть земной поверхности, как бы вырезанная из полушария, цилиндра или сектора. При этом рамки географической карты могут быть произвольными, а на топографических они совпадают с меридианами и параллелями.
Источник
Способы получения проекций
Существует два основных способа построения картографических проекций:

Линии сопряжения касательной или секущей поверхности с поверхностью эллипсоида, называются стандартными параллелями или линиями нулевых искажений.
При проектировании точек земной поверхности на плоскость, получаем перспективные проекции. В зависимости от удаления точки глаза от центра земной поверхности, все перспективные проекции подразделяются на:
а) гномонические (центральные) – точка зрения совпадает с центром земной сферы
б) стереографические — точка зрения находится на поверхности сферы

в) ортографические – рассматривает поверхность из любой точки вне земной сферы. Получается путем проектирования точек земной сферы пучком параллельных прямых лучей, ортогональных к картинной плоскости.

Этот способ построения проекций основан на формулах, устанавливающих функциональную зависимость между точками первой и второй поверхности, имеющих следующий вид:
Аналитический способ построения проекций является более гибким, позволяет получить огромное множество новых проекций, позволяет изыскивать проекции по заранее заданному характеру искажения.
Классификация картографических проекций
Известно, что признаков для классификации может быть несколько, следовательно, и классификаций может быть несколько; при этом следует заметить, что одни и те же проекции в зависимости от признака могут попасть в разные группы. В настоящее время в нашей стране пользуются классификацией Каврайского. Согласно ей все проекции классифицируются по четырем признакам:
Виду меридианов и параллелей нормальной сетки
Положению полюса нормальной системы координат
По характеру искажения
Самым существенным признаком проекций является свойство изображений. Неизбежным же свойством изображений являются искажения. Характер искажений определяется в зависимости от того, что искажается – длина, угол или площадь. Если величина искажений в большей или меньшей степени зависит от размеров и формы изображаемой территории, то характер искажений всецело зависит от самой проекции. Вот почему при выборе проекции решающую роль играет характер искажений.
По характеру искажения проекции делятся на:
Равноугольные (конформные) – углы и азимуты передаются без искажений, т.к. масштабы длин в точках не зависят от направления. Как следствие, в этих проекциях сохраняется подобие в бесконечно малых частях. Картографическая сетка в этих проекциях ортогональна. На картах в равноугольных проекциях можно измерять углы и азимуты, на них удобно производить измерение длин по всем направлениям.
Равновеликие (эквивалентные) – масштаб площадей остается постоянным и равным единице, а следовательно площади передаются без искажений. На картах в равновеликих проекциях можно делать сопоставление площадей.
Равнопромежуточные (эквидистантные) – масштаб по одному из главных направлений сохраняется и равен единице (а=1 или b=1)
Произвольные – присутствуют все виды искажений.
Свойства равноугольности, равновеликости, равнопромежуточности одновременно на одной и той же проекции несовместимы. Проекции, на которой всюду отсутствовали бы искажения длин, т.е. было бы сохранено постоянство масштаба, не существует. На карте могут отсутствовать либо искажения углов, либо площадей, но одновременно отсутствовать искажения углов и площадей не могут. Поэтому характерным свойством картографической проекции является обязательное наличие на карте того или иного искажения.
По виду меридианов и параллелей нормальной сетки
Классификация проекций по виду нормальной сетки наиболее наглядна и наиболее проста, и поэтому она легче всего воспринимается. Следует подчеркнуть, что классификация по этому признаку касается только проекций в нормальном положении, вид косых или поперечных сеток будет уже другой, не охватываемый классификацией.
По виду меридианов и параллелей нормальной сетки:
Круговые – проекции, у которых меридианы и параллели изображаются окружностями. Экватор и ср. меридиан – прямые линии. Применяются для изображения всей поверхности Земли. (произвольная Гринтена, равноугольная Лагранжа).
Азимутальные – параллели – одноцентренные окружности, меридианы – пучок прямых, расходящихся радиально из центра параллелей. Эти проекции применяются в прямом положении — для полярных территорий; в поперечном — для изображения зап. и вост. полушарий; в косом — для изображения территорий, имеющих округлую форму.
Цилиндрические – параллели — параллельные прямые, перпендикулярные осевому меридиану, причем параллели всегда равноразделенные (отрезки параллелей пропорциональны разностям долгот); меридианы — Все меридианы прямые,
перпендикулярные параллелям. Расстояния между меридианами пропорциональны разностям долгот. В этих проекциях можно изобразить весь земной шар. Наиболее выгодны эти проекции для изображения территорий, расположенных вблизи экваториальных широт и растянутых вдоль экватора (или вдоль некоторой стандартной параллели).
Конические – параллели — Дуги концентрических окружностей, общий центр которых лежит на осевом меридиане или его продолжении. Параллели равноразделенные, т.е.вдоль каждой параллели отрезки между меридианами одинаковые; меридианы — пучок прямых, расходящихся радиально из точки, являющейся центром параллелей. Углы между меридианами пропорциональны разностям их долгот. Эти проекции наиболее выгодны для изображения территорий, расположенных в средних широтах и растянутых вдоль параллелей.
Псевдоконические – параллели — дуги концентрических окружностей, общий центр которых лежит на осевом меридиане или его продолжении; меридианы – некоторые кривые, симметричные относительно среднего прямолинейного меридиана. Наиболее выгодны для изображения территорий, имеющих форму квадрата с вогнутыми сторонами. (проекция Бонна – применяется для карты Франции).
Псевдоцилиндрические – параллели — Параллельные прямые, перпендикулярные осевому меридиану. В большинстве случаев равноразделенные; меридианы – некоторые кривые, симметричные относительно среднего прямолинейного меридиана. Используются для изображения всей земной поверхности. Наиболее выгодны для изображения территорий растянутых вдоль среднего меридиана и экватора. (равновеликая синусоидальная проекция Сансона, равновеликая синусоидальная проекция Эккерта, равновеликая эллиптическая проекция Мольвейде). 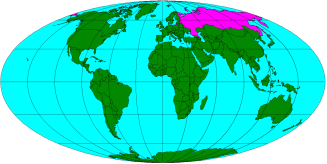

Поликонические – параллели — дуги окружностей (окружности), центры которых лежат на осевом меридиане сетки или на его продолжении; меридианы – некоторые кривые, симметричные относительно среднего прямолинейного меридиана. Широко применяются для мелкомасштабных обзорных карт, выгодны для изображения территорий, растянутых вдоль среднего меридиана. (простая поликоническая проекция, видоизмененная поликоническая проекция для международной карты мира в масштабе 1:1 000 000).
Источник