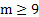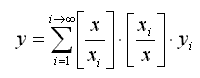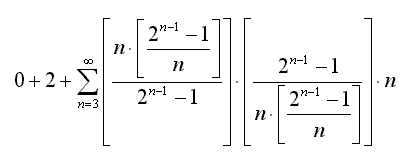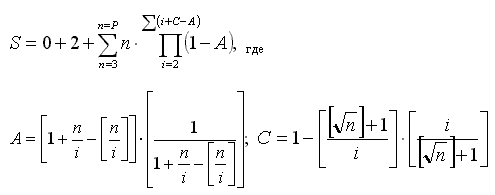Способы получения простых чисел

Получение простых чисел

По мере того как мы будем изучать курс «Математические основы криптологии» мы будем возвращаться к этой теме.

Задача получение простых чисел во многом зависит от того как ставить эту задачу.

1)Разложение. Самый древний способ получения простых чисел, как мы уже знаем, — решето Эратосфена. но максимум получение чисел на современной вычислительной технике по этому способу, это N=10 12 .

2) Формульный метод. С помощью формул можно получить некоторое множество чисел, но оно ограниченно. Простейшие:

а) целочисленные полиномы (в общем случае не решают задачу получение бесконечного множества простых чисел.)

б) экспоненциальная функция. (множество получаемое на основе данного способа, как мы уже говорили, ограничено по мощности.

этот способ имеет больший интерес для анализа криптошифра.

в) прамориальная формула. Пока не известно можно ли по этой формуле получить бесконечное число простых чисел.

Задано некоторое число m и проверяется по определенному алгоритму, является ли оно простым. Так называемое тестирование на простоту. Этот способ используется в современных криптографических системах с открытым ключём. Берется некоторое большое число (сотни десятичных знаков) и по отношению к этому числу начинается тестирование.

Существует 2 метода тестирования на простоту:

отвечают на вопрос простое или составное однозначно.

2)вероятностные тесты. С помощью них мы можем говорить только с некоторой вероятностью, что данное число простое. При этом вероятность может быть сколь угодна близка к единице. Но эти методы гораздо быстрее, нежели строгие, по отношению к большим числам. Т.е. когда информация не столь важна(для шифрование) мы можем рискнуть, и с некоторой вероятностью, использовать вместо простого числа составное.

Метод, объединяющий в себе как вероятностные, так и детерминированные методы называется комбинированным методом. Т.е. сначала мы выясняем, с некоторой вероятностью, что число m простое и потом по отношению к нему применяем строгий метод и в итоге это более оптимально чем сразу применять к некоторому большому числу строгий тест.

С понятием «строгие тесты» связанно такое понятие как «факторизация».

Факторизация – разложение заданного числа на простые сомножители.

Одним из первых методов факторизации является метод разложение чисел Мерсена [M(p)]. Еще в 19 веке был предложен тест проверки чисел Мерсена на простоту. Это был один из первых строгих тестов.

Так как же определить является ли число Мерсена простым или составным? Существует метод, причем достаточно эффективный для больших чисел.

Тестирование чисел Мерсена М(р)

Дано число Мерсена. М(р)

1. Получаем последовательность определенных целых чисел S₁,S₂,…S_p_-2 Получаем ее по правилу S_i₊₁=S_i 2 -2. Т.е. каждый последующий член последовательности равен квадрату предыдущего минус 2.

Но при этом задается S₀=4. Тогда при р=5:М(р)=31S₀=4 S₁=14, S₂=(14 2 -2) 2 -2. Казалось бы идет быстрое нарастание чисел, что представляет определенную сложность для дальнейших вычислений, но в Теории чисел есть определенные «хитрости» которые мы рассмотрим в дальнейшем.

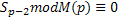
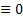
, если то число простое (т.е. без остатка)

если в остатке есть некоторое число , то число составное. Причем остаток меньше чем М(р).

Вопрос заключается в том, как можно эффективно реализовать эту операцию при больших числах Мерсена. Ответ на этот вопрос существует , но сейчас нам сложно его объяснить , рассмотрим эту модульную операцию в последующих лекциях. На этой операции буквально и держится вся криптография. Она применяется по отношению к определенным функциям. Почти все известные методы тестирования тоже основаны на этой операции. Как современные так и древние. Какими свойствами обладает эта операция и ее приложение , мы посветим этому несколько лекций позднее.

Рассмотрим алгоритм факторизации (алгоритм Ферма).

Задано число, мы пытаемся его разложить. Если раскладывается, то составное, если нет, то простое.

Тоже определенная форма строгого теста.

1) Задано число m, причем

Возникает вопрос: Бесконечно ли можно продолжать этот ряд. Ответ: Нет.

С каждым членом (m_i) проводим следующую операцию. Можно ли его представить в виде квадрата некоторого числа.

Если можно то мы останавливаем процесс и

m= (t-i)(t+i) и причем (t-i) – это p₁ ,а p₂= (t+i) , где p₁ и p₂ — простые сомножители.

Но этот алгоритм действует только до определенных границ:

Ограничение

Если исходное число велико, то это сокращает число членов в 6 раз. Если рассмотреть на оси точки которые является квадратами некоторых чисел, то число квадратов гораздо больше чем число простых чисел и на квадраты мы натыкаемся гораздо быстрее.

Если до величины 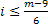мы не нашли квадрата, то мы останавливаемся.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Способы получения простых чисел

ТЕОРИЯ ЧИСЕЛ: ПРОСТЫЕ ЧИСЛА И УНИВЕРСАЛЬНОЕ УРАВНЕНИЕ

Для описания самых сложных и трудно поддающихся описанию формулами процессов и объектов может применяться универсальное уравнение:

где [ ] — (и далее по тексту) математический знак обозначающий целую часть числа.

Известно, что в теории чисел на протяжении очень длительного времени не удается предложить формулу (в традиционном ее понимании и представлении) задающую последовательность простых чисел из-за непредсказуемости их появления в общей последовательности чисел. В настоящее время последовательности простых чисел описываются либо в виде баз данных (списков, таблиц, массивов) простых чисел, либо в виде компьютерных программ (алгоритмов) позволяющих находить простые числа по тем или иным правилам.

Учитывая широкие возможности универсального уравнения можно ожидать, что его применение позволит продвинуться в вопросе представления одной формулой последовательности простых чисел. Поскольку этот вопрос является весьма сложным ниже рассмотрены лишь возможные подходы к описанию последовательности простых чисел формулой, составленной на основе использования универсального уравнения.

Самым простым и очевидным способом использования универсального уравнения при описании последовательности простых чисел является непосредственное задание этим уравнением последовательности простых чисел на основе таблицы известных простых чисел путем замены x¡ на порядковый номер n простого числа в последовательности простых чисел, а y¡ на значение этого простого числа:

При подстановке в такое уравнение какого либо порядкового номера n простого числа в общей последовательности простых чисел будет вычисляться значение простого числа соответствующее этому порядковому номеру. Это уравнение можно продолжать до бесконечности и очевидны его главные недостатки — значительный объем и большие затраты времени на выполнение вычислений с его использованием. Хотя вполне могут возникнуть ситуации его практического использования, например при нежелательности применения таблиц (массивов) простых чисел, использовании лишь фрагментов уравнения.

При использовании универсального уравнения совместно с малой теоремой Ферма для задания числового ряда:

0 + 2 + 3 + 0 + 5 + 0 + 7 + 0 + 0 + 0 + 11 + 0 + 13 + 0 + 0 + 0 + 17 + 0 + 19 + 0 + 0 + 0 + 23 + 0 + 0 + 0 + 0 + 0 + 29 + 0 + 31 + 0 + 0 + 0 + 0 + 0 + 37 + 0 + 0 + 0 + 41 + 0 + 43 + 0 + 0 + 0 + 47 + 0 + 0 + 0 + 0 + 0 + 53 + 0 + 0 + 0 + 0 + 0 + 59 + 0 + 61 + 0 + 0 + 0 + 0 + 0 + 67 + 0 + 0 + 0 + 71 +.

в котором все члены не равные простым числам равны нулю можно получить формулу существенно меньшего объема:

Нетрудно заметить, что в этой формуле с ростом n слишком быстро будут расти объемы вычислений и используемые при вычислениях по формуле числа.

Рост объема вычислений с увеличением n при формировании ряда можно несколько замедлить если при составлении формулы для вычисления членов ряда совместно с универсальным уравнением использовать тест простоты числа n заключающийся в проверке его на делимость на все простые числа меньшие, чем корень из n. При этом формула, задающая числовой ряд увеличится в объеме и будет иметь следующий вид:

P — порядковый номер выбранного предельного члена ряда. В этой формуле применение универсального уравнения обеспечило изменение верхнего предела произведения в ходе выполнения вычислений.

Для того, что бы посмотреть, как работает формула на форме в Visual Basic создайте кнопку и загрузите в нее следующий код, имитирующий использование формулы:

Изменяя в представленном коде значение P будете получать значение ряда и частичную сумму ряда для N от 0 до P. Причем представленный код полностью имитирует вычисления по формуле в ручную.

Демонстрационную версию программы можно посмотреть на http :// stob 2. narod . ru / program / prost . htm .

Если поэкспериментировать с рассматриваемой формулой, то не трудно будет заметить, что рассчитанное для любого n значение частичной суммы ряда будет находиться в окрестностях простого числа. Используя это свойство можно предложить следующую формулу для вычисления по заданному числу значения простого числа большего заданного:

Представленный код не содержит операторов управления порядком выполнения команд. Таких, например, как If . Then. Что характерно при выполнении вычисления по формуле и не характерно при выполнении вычислений по алгоритму. Это доказывает, что рассматриваемое выражение действительно является математической формулой (уравнением), а не просто записанным особым образом алгоритмом.

Демонстрационную версию программы можно посмотреть на http :// stob 2. narod . ru / program / prost . htm .

При изменении в представленном коде значения P в результате вычислений по программе будет получаться новое простое число W большее P. Например, при подстановке значений Р в интервале от 641 до 647 по формуле можно вычислить ряд простых чисел, приведенных в таблице:

W 33629 33629 34273 34273 34373 34273 34919

Числа 641, 643, 647 являются простыми. Как видно из таблицы формула позволяет вычислить новые простые числа только для Р тоже простых.

Необходимо учитывать, что сумма S всех простых чисел ряда от 1 до Р тем больше отличается от вычисленного W, чем больше Р и соответственно W. Исходя из этого для уменьшения объема вычислений в формулу можно ввести поправочные коэффициенты, зависящие от величины P и W.

Необходимо еще отметить, что приведенные в этой статье программы не позволяют вычислять по настоящему большие числа. Для этого необходимо дополнительно использовать специальные методы работы на ПЭВМ с большими числами. В интернете быстро можно найти описание соответствующих методов и программ.

При изменении в представленном коде рассматриваемой формулы значения P в результате вычислений по программе будет получаться новое простое число W большее P. Например, при P = 2 W = 3, при P = 20 W = 79, при P = 201 W = 4229, при P = 199991 W = 1709400841, при P = 199999 W = 1709600813, при P = 200000 W = 1709600813.

Приведенные примеры показывают, что данная формула в любом случае позволяет всегда вычислить простое число и в этом смысле она является более эффективной, чем традиционно применяемый в криптографических системах для получения случайных простых чисел алгоритм, который, как известно, не всегда сразу позволяет найти простое число.

Очевидно, что если в формулу последовательно подставлять числа натурального ряда 2, 3, 4, 5, 6, 7. то ряд натуральных чисел будет преобразован в бесконечный ряд, состоящий только из простых чисел. Фрагмент такого ряда приведен в следующей таблице:

Несмотря на то, что рассматриваемая формула не позволяет вычислить подряд все простые числа, анализ таблицы позволяет утверждать, что данная формула все же выражает функциональную связь каждого члена ряда натуральных чисел с конкретным простым числом.

Кроме этого, так как формула позволяет вычислить новые простые числа только для Р тоже простых, то ее можно использовать для тестирования абсолютно всех чисел на простоту. Поскольку очевидно, что если при помощи формулы для некоторого числа Р вычислить значение W 1 , а затем вычислить значение W 2 для числа Р-1 и если в результате окажется, что W 1 = W 2 , то число Р является составным, а если W 1 будет отличаться от W 2 , то число Р будет являться простым.

Так, например, для числа Р = 75353 W 1 = 264480091, а для числа Р — 1 = 75353 — 1 = 75352 W 2 = 264404731. Так как W 1 и W 2 отличаются друг от друга, то исходя, из выше приведенных рассуждений, число 75353 будет являться простым числом.

Для числа Р = 75367 W 1 = 264555491, а для числа Р — 1 = 75367 — 1 = 75366 W 2 = 264480091. Так как W 1 и W 2 отличаются друг от друга, то исходя, из выше приведенных рассуждений, число 75367 так же будет являться простым числом.

А вот для числа Р = 75361 W 1 = 264480091, и для числа Р — 1 = 75361 — 1 = 75360 W 2 = 264480091. Так как W 1 = W 2 , то исходя, из выше приведенных рассуждений, число 75361 будет являться составным числом.

Действительно число 75361 можно разложить на следующие простые множители: 75361 = 11 · 13 · 17 · 31.

Более того, так как значение W изменяется только при достижении числа 75367, то можно утверждать, что между простыми числами 75353 и 75367 будут располагаться только составные числа.

Необходимо так же отметить, что число 75361 является псевдопростым числом, то есть является натуральным числом, обладающим некоторыми свойствами простых чисел. Относится к псевдопростым числам Ферма или, к так называемым, числам Кармайкла. Эти числа способны пройти тест простоты, основанный на малой теореме Ферма. Но рассматриваемая формула, выражающая строгую функциональную связь между рядом натуральных чисел и рядом простых чисел, естественно лишена этого недостатка и позволяет однозначно определять псевдопростые числа, как составные числа.

Вообще-то на фоне представлений о непредсказуемости, хаотичности и случайности появления простых чисел в ряду натуральных чисел само существование представленных в данной статье формул выглядит довольно странным. Проще говоря, этих формул не должно было бы быть. Но они существуют.

В этой связи необходимо отметить, что о существовании статистической закономерности в распределении среди натуральных чисел простых чисел известно уже сравнительно давно. Еще в 1792-1793 годах Гаусс эмпирическим путем обнаружил, что число простых чисел на отрезке от единицы до некоторого числа в среднем близко к величине обратно пропорциональной его логарифму. В дальнейшем для изучения закономерности распределения простых чисел оформился специальный раздел теории чисел. Правда все исследования в рамках этого раздела фактически свелись либо к уточнению вида функции распределения простых чисел, либо к обоснованию существования этой функции в различных ее представлениях.

Однако немецкий математик Бернхард Риман смог обнаружить, что функция распределения простых чисел — количество простых чисел, не превосходящих некоторое заданное число, выражается через распределение так называемых нетривиальных нулей дзета-функции. И сформулировал гипотезу: ‘Все нетривиальные нули дзета-функции имеют действительную часть, равную 1/2’, то есть являются комплексными числами, расположенными на прямой х=1/2, проходящей сквозь дзета-функцию.

Данная гипотеза Римана фактически равносильна утверждению, что распределение простых чисел основано на определенном правиле, а не на чистой случайности. А это означает, что существование приведенных в данной статье формул и им подобных все же вполне возможно.

Правда, несмотря на то, что свою гипотезу Риман сформулировал еще в 1859 году, доказать ее пока не удалось. С другой стороны существование рассматриваемых формул ведь можно рассматривать в качестве косвенного доказательства гипотезы Римана.

Тут необходимо отметить, в математике утвердилось стойкое представление о том, что все формулы, позволяющие осуществлять вычисление простых чисел, либо ограничены (позволяют вычислять простые числа на ограниченных интервалах), либо фактически представляют собой различные модификации метода (алгоритма) решета Эратосфена. Именно по этой причине выше было уделено определенное внимание обоснованию того, что рассматриваемые формулы являются именно математическими формулами, а не представленными особым образом алгоритмами.

Несмотря на то, что представление об обязательной непредсказуемости появления простых чисел и значительных затратах времени на тестирование простоты больших чисел не было строго обосновано, простые числа стали широко использоваться в криптографии (различных системах шифрования), в системах электронной подписи, в различных сетевых протоколах и технических средствах защиты. Изложенные в настоящей статье сведения указывают на то, что такая беспечность в конечном итоге может дорого обойтись. И специалистам по защите информации, охране государственной и коммерческой тайн и вообще всякой секретной информации, по обеспечению надежного функционирования различных технических устройств (в первую очередь средств связи, передачи данных и платежных систем) и предотвращению их взлома, а также разработчикам различных криптосистем, систем шифрования и криптоаналитикам следовало бы уже сейчас побеспокоиться о надежности используемых ими математических методах.

Источник