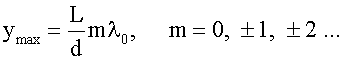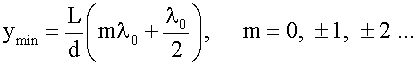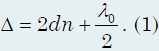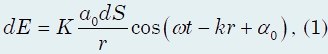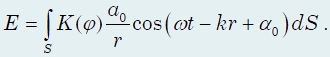Способы получения пространственных когерентных волн
Способы получения когерентных волн
Основная задача двухлучевой интерференции.
Тепловые источники некогерентны друг другу. Для получения когерентных световых волн, волну, излучаемую одним источником света, разделяют на две, и затем полученные волны сводят вместе в некоторой области пространства, называемой областью перекрытия. Для того, что бы возникла устойчивая интерференционная картина, разность хода ∆ этих волн до области перекрытия не должна превышать некоторой характерной длины, называемой длиной когерентности (более подробно этот вопрос рассматривается в лекции 2).
Образовавшиеся после разделения волны в стандартных двухлучевых интерференционных установках можно рассматривать как исходящие из двух точечных когерентных источников и . Как правило, по крайней мере, один из источников мнимый. Возможна ситуация, когда источники удалены на бесконечность – интерференция плоских волн.
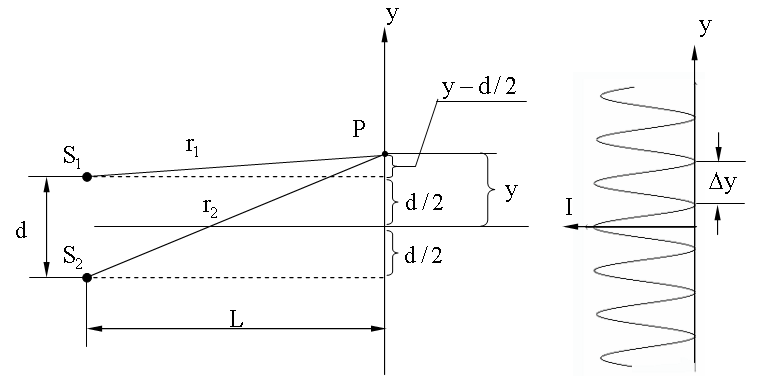
Схема основной задачи двухлучевой интерференции изображена на рис. 1.5.
где — угол зрения, под которым видны оба источника из центра экрана, .
Первым интерференционным опытом, получившим объяснение на основе волновой теории света, явился опыт Юнга (1802 г.). Источником света является освещенная щель S, от которой световая волна падает на две узкие щели S1 и S2, освещаемые различными участками одного и того же волнового фронта (Рис.1.5). Проходя через каждую из щелей, световой пучок уширялся вследствие дифракции, поэтому на белом экране Р световые пучки, прошедшие через щели S1 и S2, перекрывались. В области перекрытия световых пучков наблюдалась интерференционная картина в виде чередующихся светлых и темных полос.
Юнг был первым, кто понял, что нельзя наблюдать интерференцию при сложении волн от двух независимых источников. Поэтому в его опыте щели S1 и S2, которые в соответствии с принципом Гюйгенса можно рассматривать как источники вторичных волн, освещались светом одного источника S. Юнг первый наблюдал осуществленное таким способом явление интерференции и первый в математически корректной форме установил принцип суперпозиции амплитуд как суть явления интерференции. При симметричном расположении щелей вторичные волны, испускаемые источниками S1 и S2, находятся в фазе, но эти волны проходят до точки наблюдения P разные расстояния r1 и r2, следовательно, фазы колебаний, пришедших от источников S1 и S2 в точку P, вообще говоря, различны. Таким образом, задача об интерференции волн сводится к задаче о сложении колебаний одной и той же частоты, но с разными фазами. Утверждение о том, что волны от источников S1 и S2 распространяются независимо друг от друга, а в точке наблюдения они просто складываются, является опытным фактом, и получило определение как принцип суперпозиции.
Интересно, однако, что сходный, по сути, опыт был выполнен еще в 1665 г. Гримальди, в котором отсутствовала щель S, и в качестве источника света использовались прямые солнечные лучи. Расчет показывает, что в виду значительных угловых размеров ( 0,01 рад ) Солнца при расстоянии между щелями S1 и S2 превышающем 0,05 мм интерференционная картина не возникает в виду нарушения условия пространственной когерентности: При характерной длине волны света и получаем результат . Весьма сомнительно, чтобы Гримальди смог реализовать на практике столь незначительное расстояние между щелями.
Остроумие установки Юнга заключается именно в том, что, внеся, казалось бы, лишний элемент – дополнительный экран с отверстием S , он сумел уменьшить угловые размеры источника света. При апертурных размерах отверстия S равных 0,1мм на расстоянии в 1 м между дополнительным экраном S и экраном с двумя щелями и получаем угловые размеры источника света, то есть отверстия S, равные .При этих условиях расстояние между щелями в 2 мм является допустимым для получения интерференционной картины.
В современных демонстрационных установках опыта Юнга в качестве источника света используют луч лазера, при этом дополнительный экран с отверстием S оказывается излишним, экран с двумя отверстиями и облучают непосредственно лучом лазера в виду его высокой пространственной когерентности. Таким образом, опыт Гримальди через три столетия состоялся, но на совершенно другом технологическом уровне. Облучение отверстий лучом лазера дает громадный выигрыш в освещенности, что позволяет использовать опыт в демонстрационных учебных установках.
Источник
Способы получения когерентных волн.
Получение когерентных волн для реализации интерференции в оптике осуществляется двумя способами:
1.инструментальное получение из данного источника двух когерентных;
2.деление фронта волны.
Схемы получения когерентных волн в первом случае основаны на получении двух источников, которые являются двумя изображениями данного единого излучающего центра (метод Юнга, бипризма Френеля, зеркала Френеля). Во втором случае получение когерентных волн происходит делением волны в пределах цуга на две волны (интерферометр Майкельсона, тонкие пленки, клин, кольца Ньютона).
23. Интерференция. Условия максимума и минимума интерференции. Опыт Юнга.
Интерференция.
Интерференцией световых волн называется сложение двух когерентных волн, вследствие которого наблюдается усиление или ослабление результирующих световых колебаний в различных точках пространства.
Условия максимума и минимума интерференции.
Опыт Юнга.
В этом опыте Юнг поток света направил на непрозрачную пластинку с двумя очень маленькими отверстиями, за которой находился экран. Если придерживаться господствовавшей в то время корпускулярной теории света, то на экране он должен был увидеть две светящиеся точки. Вместо этого на экране он увидел чередующиеся светлые и тёмные полосы. Причём самая яркая из них находилась на экране посередине между отверстиями на перегородке, чего быть вообще-то не должно. Юнг объяснил возникновение полос явлением интерференции света.
Но мы с вами ранее сказали, что интерференция — это сложение в пространстве двух или нескольких волн. Таким образом, мы, вслед за Юнгом, можем сказать, что свет обладает волновыми свойствами.
На экране светлые полосы соответствуют точкам, в которых фазы волн одинаковы, а тёмные — точкам, в которых фазы волн противоположны. Существует формула, по которой можно рассчитать, в каком месте экрана будет светлая, а в каком тёмная полоса:
Как видно из формул, расположение максимумов и минимумов на экране будет зависеть от расстояния между источниками (d), расстояния от источников до экрана (L) и от длины волны λ0
24. Интерференция. Условия максимума и минимума интерференции. Кольца Ньютона.
Кольца Ньютона.
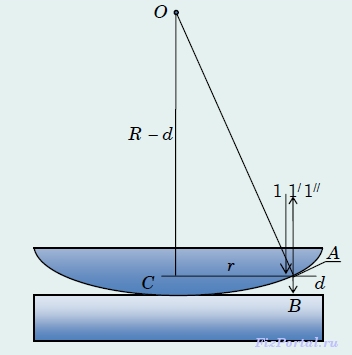
Классическим примером полос равной толщины являются кольца Ньютона. Они наблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельной стеклянной пластинки большой толщины и плоско-выпуклой линзы большого радиуса кривизны. Роль тонкой пленки, от которой отражаются когерентные волны, играет воздушный зазор между пластинкой и линзой. Падающий луч 1 отражается в точках А и В (рис.) от верхней и нижней поверхности воздушного клина и образует отраженные лучи 1 / и 1 // , имеющие разность хода:
25. Интерференция. Условия максимума и минимума интерференции. Плоскопараллельная пластинка.
Плоскопараллельная пластина.
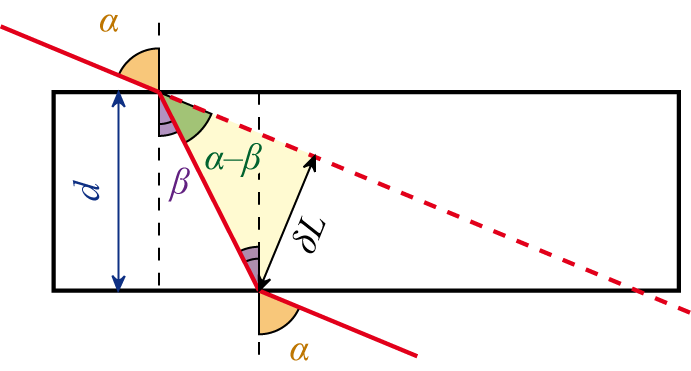
Плоскопараллельная пластина — это оптический прибор, представляющий собой ограниченный параллельными поверхностями слой однородной среды, прозрачной в некотором интервале длин волн λ оптического излучения. Основным оптическим свойством пластины является то, что луч, падающий на пластину, в результате двукратного преломления на поверхностях пластины параллельно смещается на некоторую величину δL относительно исходного луча (см. рисунок).
Плоскопараллельную пластину можно рассматривать в качестве сферической линзы, ограниченной поверхностями бесконечного радиуса. Для такой линзы величина оптической силы равна нулю. Именно поэтому обычные оконные стекла не искажают изображения, а лишь немного смещают его. Но такой сдвиг незаметен глазу, поскольку сдвигается все изображения в поле зрения.
26. Интерференция. Условия максимума и минимума интерференции. Тонкий клин.
27. Дифракция. Виды дифракции. Принцип Гюйгенса-Френеля.

Дифракция.
Под дифракцией света понимают явление непрямолинейного распространения света, проникновение его в область геометрической тени, огибание им препятствий.
Виды дифракции.
1. Дифракция на круглом отверстии (дифракция Френеля).
2. Дифракция от щели (дифракция Фраунгофера).
3. Дифракционная решётка.
Принцип Гюйгенса-Френеля.
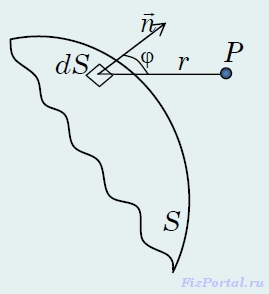
Согласно принципу Гюйгенса-Френеля световая волна, возбуждаемая каким-либо источником S может быть представлена как результат суперпозиции когерентных вторичных волн. Каждый элемент волновой поверхности S (рис.) служит источником вторичной сферической волны, амплитуда которой пропорциональна величине элемента dS.
Амплитуда этой вторичной волны убывает с расстоянием r от источника вторичной волны до точки наблюдения по закону 1/r. Следовательно, от каждого участка dS волновой поверхности в точку наблюдения Р приходит элементарное колебание:
где (ωt + α0)− фаза колебания в месте расположения волновой поверхности S, k− волновое число, r − расстояние от элемента поверхности dS до точки P, в которую приходит колебание. Множитель а0 определяется амплитудой светового колебания в месте наложения элемента dS. Коэффициент K зависит от угла φ между нормалью к площадке dS и направлением на точку Р. При φ = 0этот коэффициент максимален, а при φ/2он равен нулю.
Результирующее колебание в точке Р представляет собой суперпозицию колебаний (1), взятых для всей поверхности S:
Эта формула является аналитическим выражением принципа Гюйгенса-Френеля.
28. Метод зон Френеля (на примере сферической волны). Условия дифракционного максимума и минимума. Дифракция на малом отверстии.
Метод зон Френеля (на примере сферической волны).
Френель предложил метод разбиения фронта волны на кольцевые зоны, который впоследствии получил название метод зон Френеля.
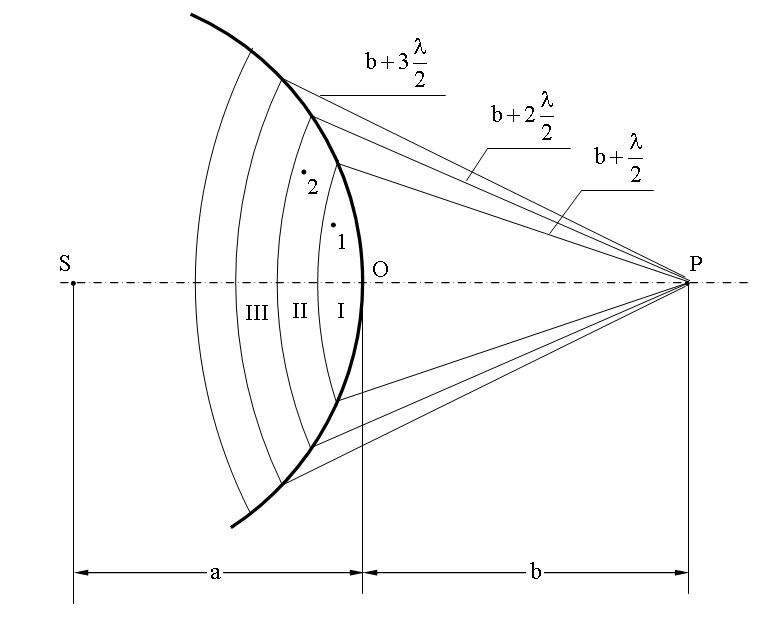
Пусть от источника света S распространяется монохроматическая сферическая волна, P — точка наблюдения. Через точку O проходит сферическая волновая поверхность. Она симметрична относительно прямой SP.
Разобьем эту поверхность на кольцевые зоны I, II, III и т.д. так, чтобы расстояния от краев зоны до точки P отличались на l/2 — половину длины световой волны. Это разбиение было предложено O. Френелем и зоны называют зонами Френеля.
Возьмем произвольную точку 1 в первой зоне Френеля. В зоне II найдется, в силу правила построения зон, такая соответствующая ей точка, что разность хода лучей, идущих в точку P от точек 1 и 2 будет равна l/2. Вследствие этого колебания от точек 1 и 2 погасят друг друга в точке P.
Из геометрических соображениях следует, что при не очень больших номерах зон их площади примерно одинаковы. Значит каждой точке первой зоны найдется соответствующая ей точка во второй, колебания которых погасят друг друга. Амплитуда результирующего колебания, приходящего в точку P от зоны с номером m, уменьшается с ростом m, т.е.

Последнее изменение этой страницы: 2017-03-14; Просмотров: 3406; Нарушение авторского права страницы
Источник
2.3. Способы получения когерентных волн
Очевидно, что получить когерентные волны от двух независимых источников света практически невозможно. Это связано с тем, что свет атомом излучается в процессе перехода электронов атома с одного энергетического уровня на другой. Момент такого перехода носит вероятностный характер, соответственно, случайна фаза излучаемой атомом электромагнитной волны. Излучение источника складывается из совокупности излучений отдельных атомов и фаза его, естественно, меняется случайным образом. Следовательно, независимые источники излучают световые волны, разность фаз которых меняется хаотично.
Когерентные волны можно получить, если излучение одного источника разделить на два пучка, заставить каждый пучок пройти разные оптические пути, а затем наложить их друг на друга. В этом случае фазы световых волн в каждом пучке меняются хаотично, но синхронно друг с другом, т.е. разность фаз остается постоянной, и пучки будут когерентными. Такое разделение можно осуществить двумя способами — делением волнового фронта и делением амплитуды волны. Способы деления амплитуды волны будут рассмотрены далее, а в данном пункте рассмотрим несколько конкретных интерференционных схем, в которых используется метод деления световой волны по фронту.
Схема Юнга. Пучок света падает на непрозрачный экран с узкой щелью (рис.2.3). Прошедшим светом освещаются две узкие параллельные щели во втором непрозрачном экране. На этих щелях свет испытывает дифракцию, в результате чего за щелями получаются два расходящихся световых пучка. Эти пучки когерентные, т.к. исходят от одного источника. В области их перекрытия АВ наблюдается интерференционная картина.
Бизеркала Френеля. Два плоских соприкасающихся зеркала (рис.1.2) установлены так, что угол между их плоскостями близок к 180 О . Зеркала освещаются светом от источника S (как правило, в качестве источника берется узкая светящаяся щель, ориентированная параллельно линии соединения зеркал). При отражении от зеркал падающий свет разделяется на две когерентные цилиндрические волны, распространяющиеся так, как если бы они исходили из мнимых источников S1 и S2, являющихся изображением источника в каждом из зеркал. На экране, где волны перекрываются, наблюдается интерференционная картина.
Бипризма Френеля. Бипризма Френеля (рис.2.5) состоит из двух призм с небольшими преломляющими углами , склеенных по малым основаниям. Параллельно основаниям призм на оси симметрии системы располагается узкая светящаяся щель . После преломления в каждой из призм лучи отклоняются от своего первоначального пути на угол =(n-1), где n— показатель преломления стекла, из которого изготовлены призмы. После преломления в бипризме падающий от S пучок света разделяется на два, как бы исходящих из мнимых источников S1 и S2, находящихся в точках пересечения продолжений преломленных лучей. На экране в области пересечения преломленных пучков АВ наблюдается интерференционная картина.
Билинза Бийе. а) Тонкая сферическая линза разрезается по диаметру, и ее половинки разводятся на небольшое расстояние. Образовавшийся промежуток между половинками линзы закрывается непрозрачным экраном. Источник света S помещается на оси симметрии системы на двойном фокусном расстоянии от линзы. В результате получают два действительных изображения S1 и S2 точечного источника S (рис.2.5). S1 и S2 являются источниками сферических когерентных волн. В области их перекрытия наблюдается интерференционная картина.
б) Из тонкой линзы вырезается по диаметру узкая полоска, а оставшиеся части склеиваются по срезу. Источник света помещается в фокусе линзы. В результате преломления лучей в половинках линзы получаем два пучка с плоскими фронтами, распространяющимися под малым углом друг к другу. В области перекрытия пучков наблюдается интерференционная картина (см. рис.2.6).
Во всех (кроме последнего) рассмотренных выше способах получения когерентных волн расчет параметров интерференционной картины сводится к уже изученному нами случаю двух когерентных источников (п.2.2). Надо только в формуле (2.14) использовать расстояние между источниками S1 и S2 и расстояние от источников до экрана, найденные с учетом особенностей геометрии каждого конкретного случая.
Источник