- Способы получения когерентных волн света
- Способы получения когерентных источников света
- Методы получения когерентных световых волн
- ВОЛНОВАЯ ОПТИКА
- 18.2. Способы получения когерентных источников
- 18.2.1. Опыт Юнга
- 18.2.2. Зеркала Френеля
- 18.2.3. Бипризма Френеля
- 18.2.4. Интерференция при отражении от прозрачных пластинок
- 18.2.4.1. Кольца Ньютона
- 18.3. Многолучевая интерференция
Способы получения когерентных волн света
3.2. Методы получения когерентных волн
Для получения когерентных световых волн с помощью обычных (нелазерных) источников применяют метод разделения света от одного источника на две или нескольких систем волн (световых пучков). В каждой из них представлено излучение одних и тех же атомов источника, так что эти волны когерентны между собой и интерферируют при наложении.
Разделение света на когерентные пучки можно осуществить с помощью экранов и щелей, зеркал и преломляющих тел. Рассмотрим некоторые из этих методов.
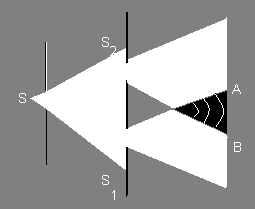
Источником света служит ярко освещенная щель S, от которой световая волна падает на две узкие щели S 1 и S 2 , параллельные щели S.
Таким образом, щели S 1 и S 2 играют роль когерентных источников. На экране Э (область ВС) наблюдается интерференционная картина в виде чередующихся светлых и темных полос.
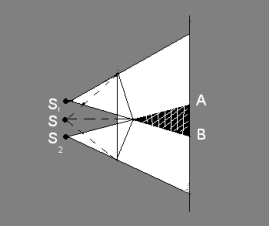
Она состоит из двух одинаковых сложенных основаниями призм. Свет от источника S преломляется в обеих призмах, в результате чего за призмой распространяются лучи, как бы исходящие от мнимых источников S 1 и S 2 , являющихся когерентными. Таким образом, на экране Э (область ВС) наблюдается интерференционная картина.
3.3. Оптическая длина пути и разность хода
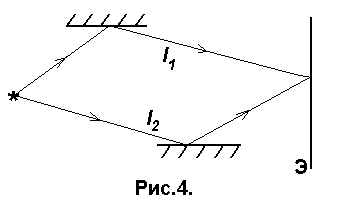
Пусть две когерентные волны (см. 3.1) создаются одним источником S, но до экрана проходят разные геометрические длины путей l 1 и l 2 в средах с абсолютными показателями преломления n 1 и n 2 соответственно (рис.4).
Тогда фазы этих волн [см. (1) и (2.9)]
w t — j 1 = w t — k 1 l 1 + j 0 , w t — j 2 = w t — k 2 l 1 + j 0
j 2 — j 1 = k 2 l 2 — k 1 l 1 = 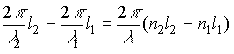
где l 1 = l /n 1 , l 2 = l /n 2 -длины волн в средах, показатели преломления которых n 1 и n 2 соответственно, l — длина волны в вакууме.
Произведение геометрической длины пути l световой волны на абсолютный показатель преломления n называется оптической длиной пути волны.
Величину 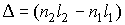
называют оптической разностью хода интерферирующих волн. С учетом этого разность фаз
j 2 — j 1 = 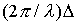
Источник
Способы получения когерентных источников света
Когерентные источники света – это источники, которые имеют постоянную во времени разность фаз, согласованное протекание нескольких колебательных или волновых процессов, степень которых различна.
Имеется много способов получения когерентных источников света, но суть их одинакова. С помощью разделения пучка на две части получают два мнимых источника света, дающих когерентные волны.
Интерференция света – сложение двух или нескольких световых волн с одинаковыми периодами, сходящихся в одной точке, в результате которого наблюдается увеличение или уменьшение амплитуда результирующей волны. Для получения устойчивой интерференционной картины необходимо, чтобы складываемые волны были когерентны. Когерентными называют волны с одинаковой частотой (периодом) и постоянной во времени разностью фаз. Чтобы получить когерентные волны необходимо световую волну от одного источника разделить на две или несколько волн. После прохождения различных путей эти волны, имея некоторую разность хода, интерферируют.
Приёмы разделения волны:
· С помощью бипризмы Френеля:
Волна, идущая от источника света, раздваивается из-за преломления света в двух половинах бипризмы. Получаемы волны 1 и 2 как бы исходят от двух мнимых источников S1 и S2 и являются когерентными, поэтому в заштрихованной области наблюдается интерференция.
Свет, проходящий через узкое отверстие S, падает на экран с двумя отверстиями S1 и S2 и делится на две когерентных волны, поэтому в заштрихованной области наблюдается интерференция, а на экране – интерференционная картина.
2. Вывод выражения для расстояния l между мнимыми изображения источника в случае бипризмы.
Бипризма Френеля представляет собой изготовленные из одного куска стекла две симметричные призмы, имеющие общее основание и малый преломляющий угол G≈1°. На расстоянии L1 от бипризмы располагается источник света S. Можно показать, что в этом случае, если преломляющий угол призмы мал и лучи падают на призму под небольшими углами, все лучи отклоняются призмой почти на одинаковый угол ϕ, равный
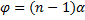
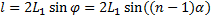
Источник
Методы получения когерентных световых волн
Вернемся к вопросу, который обсуждался уже в лекции 4.Необходимым условием интерференции волн является их когерентность, т. е. согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов. Этому условию удовлетворяют монохроматические волны — неограниченные в пространстве волны одной определенной и строго постоянной частоты. Так как ни один реальный источник не дает строго монохроматического света, то волны, излучаемые любыми независимыми источниками света, всегда некогерентны. Поэтому на опыте не наблюдается интерференция света от независимых источников, например от двух электрических лампочек. Понять физическую причину немонохроматичности, а, следовательно, и некогерентности волн, испускаемых двумя независимыми источниками света, можно исходя из самого механизма испускания света атомами. В двух самостоятельных источниках света атомы излучают независимо друг от друга. В каждом из таких атомов процесс излучения конечен и длится очень короткое время (10
8 с). За это время возбужденный атом возвращается в нормальное состояние и излучение им света прекращается. Возбудившись вновь, атом
снова начинает испускать световые волны, но уже с новой начальной фазой. Так как разность фаз между излучением двух таких независимых атомов изменяется при каждом новом акте испускания, то волны, спонтанно излучаемые атомами любого источника света, некогерентны. Таким образом, волны, испускаемые атомами, лишь в течение интервала времени 10
8 с имеют приблизительно постоянные амплитуду и фазу колебаний, тогда как за больший промежуток времени и амплитуда, и фаза изменяются.
Получить когерентные волны можно двумя способами: делением фронта волны и делением амплитуды. Оба способа сводятся к делению одной волны на две. К первому способу относятся, опыты Юнга на двух щелях, зеркала Френеля, бипризма Френеля
 Рис.5.1 Рис.5.1 |
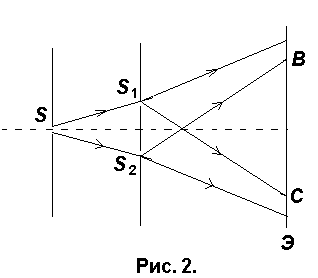
Опыт Юнга. Исторически первым интерференционным опытом, получившим объяснение на основе волновой теории света, явился опыт Юнга (1802 г.). В опыте Юнга свет от источника, в качестве которого служила узкая щель S, падал на экран с двумя близко расположенными щелями S1 и S2 (рис5.1). Проходя через каждую из щелей, световой пучок уширялся, поэтому на белом экране Э световые пучки, прошедшие через щели S1 и S2, перекрывались. В области перекрытия световых пучков наблюдалась интерференционная картина в виде чередующихся светлых и темных полос.
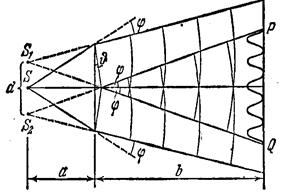 Рис.5.2 Рис.5.2 |
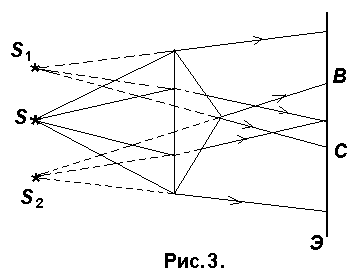
Бипризма Френеля. Изготовленные из одного куска стекла две призмы с малым преломляющим углом 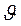
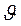
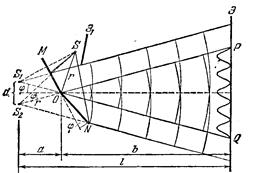 Рис.5.3 Рис.5.3 |
Зеркала Френеля. Два плоских соприкасающихся зеркала ОМ и ON располагаются так, что их отражающие поверхности образуют угол, близкий к p Соответственно угол j на рисунке очень мал. Параллельно линии ‘пересечения зеркал О на расстоянии г от нее помещается прямолинейный источник света S (например, узкая светящаяся щель). Зеркала отбрасывают на экран Э две цилиндрические когерентные волны, распространяющиеся так, как если бы Они исходили из мнимых источников S1 и S2 (рис.5.3)
Дата добавления: 2017-10-04 ; просмотров: 4831 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
ВОЛНОВАЯ ОПТИКА
|



 ,
, .
.

 .
. .
.



 .
. .
. .
. .
.


