Способы получения когерентных волн деление волнового фронта деление амплитуды

2.3. Способы получения когерентных волн

Очевидно, что получить когерентные волны от двух независимых источников света практически невозможно. Это связано с тем, что свет атомом излучается в процессе перехода электронов атома с одного энергетического уровня на другой. Момент такого перехода носит вероятностный характер, соответственно, случайна фаза излучаемой атомом электромагнитной волны. Излучение источника складывается из совокупности излучений отдельных атомов и фаза его, естественно, меняется случайным образом. Следовательно, независимые источники излучают световые волны, разность фаз которых меняется хаотично.

Когерентные волны можно получить, если излучение одного источника разделить на два пучка, заставить каждый пучок пройти разные оптические пути, а затем наложить их друг на друга. В этом случае фазы световых волн в каждом пучке меняются хаотично, но синхронно друг с другом, т.е. разность фаз остается постоянной, и пучки будут когерентными. Такое разделение можно осуществить двумя способами — делением волнового фронта и делением амплитуды волны. Способы деления амплитуды волны будут рассмотрены далее, а в данном пункте рассмотрим несколько конкретных интерференционных схем, в которых используется метод деления световой волны по фронту.

Схема Юнга. Пучок света падает на непрозрачный экран с узкой щелью (рис.2.3). Прошедшим светом освещаются две узкие параллельные щели во втором непрозрачном экране. На этих щелях свет испытывает дифракцию, в результате чего за щелями получаются два расходящихся световых пучка. Эти пучки когерентные, т.к. исходят от одного источника. В области их перекрытия АВ наблюдается интерференционная картина.

Бизеркала Френеля. Два плоских соприкасающихся зеркала (рис.1.2) установлены так, что угол между их плоскостями близок к 180 О . Зеркала освещаются светом от источника S (как правило, в качестве источника берется узкая светящаяся щель, ориентированная параллельно линии соединения зеркал). При отражении от зеркал падающий свет разделяется на две когерентные цилиндрические волны, распространяющиеся так, как если бы они исходили из мнимых источников S₁ и S₂, являющихся изображением источника в каждом из зеркал. На экране, где волны перекрываются, наблюдается интерференционная картина.

Бипризма Френеля. Бипризма Френеля (рис.2.5) состоит из двух призм с небольшими преломляющими углами , склеенных по малым основаниям. Параллельно основаниям призм на оси симметрии системы располагается узкая светящаяся щель . После преломления в каждой из призм лучи отклоняются от своего первоначального пути на угол =(n-1), где n— показатель преломления стекла, из которого изготовлены призмы. После преломления в бипризме падающий от S пучок света разделяется на два, как бы исходящих из мнимых источников S₁ и S₂, находящихся в точках пересечения продолжений преломленных лучей. На экране в области пересечения преломленных пучков АВ наблюдается интерференционная картина.

Билинза Бийе. а) Тонкая сферическая линза разрезается по диаметру, и ее половинки разводятся на небольшое расстояние. Образовавшийся промежуток между половинками линзы закрывается непрозрачным экраном. Источник света S помещается на оси симметрии системы на двойном фокусном расстоянии от линзы. В результате получают два действительных изображения S₁ и S₂ точечного источника S (рис.2.5). S₁ и S₂ являются источниками сферических когерентных волн. В области их перекрытия наблюдается интерференционная картина.

б) Из тонкой линзы вырезается по диаметру узкая полоска, а оставшиеся части склеиваются по срезу. Источник света помещается в фокусе линзы. В результате преломления лучей в половинках линзы получаем два пучка с плоскими фронтами, распространяющимися под малым углом друг к другу. В области перекрытия пучков наблюдается интерференционная картина (см. рис.2.6).

Во всех (кроме последнего) рассмотренных выше способах получения когерентных волн расчет параметров интерференционной картины сводится к уже изученному нами случаю двух когерентных источников (п.2.2). Надо только в формуле (2.14) использовать расстояние между источниками S₁ и S₂ и расстояние от источников до экрана, найденные с учетом особенностей геометрии каждого конкретного случая.

Источник

Получение когерентных пучков делением волнового фронта

Для наблюдения интерференции света от реальных (некогерентных) источников необходимо свет от одного и того же источника разделить на два пучка (или несколько пучков) и затем свести эти пучки вместе.

Способов разделения волны от первичного источника на две когерентные между собой волны два: деление волнового фронта (метод Юнга, зеркала Френеля и др.) и деление амплитуды (интерференция в тонких пленках).

Метод получения когерентных пучков делением волнового фронта (он пригоден только для достаточно малых источников) заключается в том, что исходящий из источника пучок делится на два (например, проходя через два близкорасположенных отверстия), а при наложении их друг на друга разность хода между интерферирующими лучами должна быть меньше длины когерентности.

Роль вторичных когерентных источников и играют две узкие щели, освещаемые одним источником малого углового размера, а в более поздних опытах свет пропускался через узкую щель , равноудаленную от двух других щелей. Интерференционная картина наблюдается в области перекрытия световых пучков, исходящих из и .

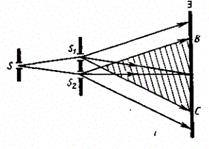
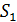
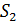
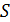
Рис. 2.2.1 Опыт Юнга

Свет от источника S падает расходящимся пучком на два плоских зеркала, расположенных относительно друг друга под углом, лишь немного отличающимся от 180° (угол мал). Световые пучки, отразившиеся от обоих зеркал, можно считать выходящими из мнимых источников S1 и S2, которые действуют как когерентные источники.

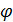
Интерференционная картина наблюдается в области взаимного перекрытия отраженных пучков.

Рис.2.2.2 Зеркала Френеля

Бипризма Френеля

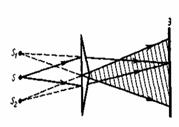
Она состоит из двух одинаковых, сложенных основаниями призм с малыми преломляющими углами. Свет от источника S преломляется в обеих призмах, в результате чего за бипризмой распространяются световые лучи, как бы исходящие из мнимых источников S1 и S2, являющихся когерентными.

Источник

Получение интерференционных картин делением волнового фронта (метод Юнга) и делением амплитуды (метод Френеля)

Вы будете перенаправлены на Автор24

Способов получения волн способных интерферировать в оптике всего два:

деление амплитуды волны,

деление фронта волны.

Метод Юнга

Для получения интерференции методом деления волнового фронта когерентные волны получают как два участка одного фронта волны.

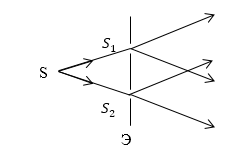
Первым, кто сконструировал установку для демонстрации явления интерференции световых волн, был Т. Юнг. При этом он использовал именно метод деления волнового фронта. Яркий пучок солнечного света попадал на экран с малым отверстием или узкой щелью. Получался как бы свет от точечного, монохроматического источника света ($S$). После дифракции на щели световая волна распространялась до двух маленьких отверстий ($S_1\ и\ S_2$), сделанных в экране ($Э$) рис.1. После очередной дифракции два расходящихся пучка света перекрывали друг друга, и так как являлись когерентными, при наложении давали интерференционную картину. При этом расстояния:

Данные отверстия работают как вторичные монохроматические, точечные источники. Световые пучки вторичных источников перекрываются за экраном $Э$ (рис.1). Картина интерференции наблюдается в области перекрывания данных световых пучков.

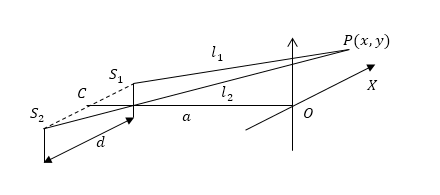
Пусть интерференционная картина наблюдается в плоскости $XOY$, перпендикулярной к нормали $CO$, проведенной к середине отрезка, соединяющего точки, в которых находятся вторичные источники света. $Ось X$ выберем параллельную отрезку $S_1S_2$ (рис.2). При этом $d$ — расстояние между отверстиями, $a$ — расстояние между отрезком $S_1S_2$ и плоскостью наблюдения.

Готовые работы на аналогичную тему

Для точки $P(x,y)$ (рис.2), которая находится в плоскости наблюдения, имеем:

Из формул (2) и (3) следует, что:

Разность путей света от источников до точки $P$ можно представить как:

Интерференционная картина будет наблюдаться только в случае, если $d\ll a$. Если $x,\ y\ll a$, то:

В таком случае имеем:

Оптическая разность хода, следовательно, равна:

При этом разность фаз имеет вид:

Так как угол $S_1PS_2$ мал, то часто считают, что волны от обоих источников движутся по одному направлению, максимумы интенсивности в таком случае будут при:

Так, интерференционная картина около точки $О$ (рис.2) состоит из интерференционных полос, которые лежат на одинаковых расстояниях и направлены под прямым углом к линии $S_1S_2$.

Необходимо отметить, что расстояние между щелями $S_<1\ >и\ S_2$ должно быть велико в сравнении с шириной щелей. Один из способов получения щелей придумал Рэлей. Он стеклянные пластинки покрывал тонким слоем серебра, делая их непрозрачными. На серебряном слое одно пластинки лезвием бритвы делалась одна линия. На другой пластинке проводили две параллельные линии. Данные линии использовались как щели.

Если применять лазеры, для опыта Юнга, то можно обойтись без первой щели.

Метод Френеля

Вторым способом создания интерференционной картины является метод деления амплитуды волны. Его смысл заключается в расщеплении волны света на полупрозрачной пластине на две когерентные волны. Фронт волны сохраняется, изменяется только направление его движения.

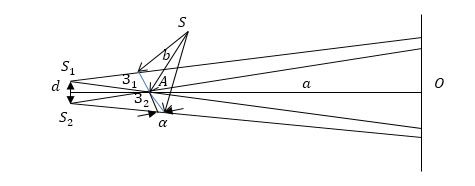
Одним из методов получения когерентных источников света в данном случае, может служить устройство, которое называют зеркалами Френеля. В этом устройстве свет от точёного источника S падает на два плоских зеркала $З_1$ и $З_2$, которые расположены под небольшим углом друг к другу ($\alpha $). При отражении свет образует два мнимых когерентных источника $S_1$ и $S_2\ (рис.3).$ Плоскость $SS_1S_2$, перпендикулярна к линии пересечения зеркал, $A$ — точка пересечения. Если расстояние $SA=b$, то $S_1A=S_2A=b$. Перпендикуляр к середине отрезка $S_1S_2$ проходит через точку $А$. Расстояние между $S_1$ и $S_2$ равно:

Угол $\varphi $, под которым из точки O видно расстояние $S_1S_2$, будет равен:

В таком случае $\triangle x$ равно:

Угол $\varphi $ можно измерить по шкале зрительной трубы. Для этого трубу размещают в точке $О$ и устанавливают ее так, чтобы отчетливо видеть изображения $S_1\ и\ S_2,\ S.\ $В таком случае легко найти длину волны $\lambda $, используя выражение:

Ширина области перекрытия световых пучков равна $2a\alpha $, значит количество интерференционных полос, которые можно наблюдать ($N$) равно:

В опыте Френеля интерференционная картина искажена дифракцией на ребре, по которому пересекаются зеркала. Полосы интерференции можно наблюдать на белом матовом экране или матовом стекле (на задней стороне).

Задание: В опыте Юнга расстояние между щелями равно $d=0,5 мм$, длина волны света $\lambda $=0,6мкм. Ширина интерференционных полос при этом равна $\triangle x=1,2\ мм.\ $Чему равно расстояние от экрана до щелей ($a$) в данном опыте?

Решение:

В опыте Юнга интерференционные максимумы наблюдаются в точках, описанных выражением:

Ширина первого интерференционного максимума при этом будет равна:

Выразим из (1.2) искомое расстояние, получим:

где для воздуха в обычных условиях $n=1$. Проведем вычисления:

Ответ: $a=1м.$

Задание: В опытах с зеркалами Френеля расстояние между мнимыми источниками света равно $d,$ расстояние от них до экрана $l$. В желтом свете ширина интерференционных полос равна $\triangle x\ .\ $Какова длина волны желтого цвета?

Решение:

Запишем условие получения интерференционных максимумов при сложении двух когерентных волн:

\[\triangle =\pm m\lambda \ \left(m=0,1,2\dots \right)\left(2.1\right),\]

где $\triangle $ — оптическая разность хода волн. Она равна (рис.4):

приравняем правые части выражений (2.1) и (2.2), получим:

\[\frac=\pm mл\to x_=\pm m\frac\lambda \left(2.3\right).\]

В таком случае запишем, что:

Ответ: $\lambda =\frac<\triangle xd>.$

Источник

10. Получение когерентных источников делением амплитуды: интерференция в тонких пленках, при отражении от тонких пластинок или кольца ньютона.

Интерференцию света по методу деления амплитуды во многих отношениях наблюдать проще, чем в опытах с делением волнового фронта. Один из способов, использующих такой метод, – опыт Поля.

В опыте Поля свет от источника S отражается двумя поверхностями тонкой прозрачной плоскопараллельной пластинки. В любую точку P, находящуюся с той же стороны от пластинки, что и источник, приходят два луча. Эти лучи образуют интерференционную картину.

Для определения вида полос можно представить себе, что лучи выходят из мнимых изображений S₁ и S₂ источника S, создаваемых поверхностями пластинки. На удаленном экране, расположенном параллельно пластинке, интерференционные полосы имеют вид концентрических колец с центрами на перпендикуляре к пластинке, проходящем через источник S. Этот опыт предъявляет менее жесткие требования к размерам источника S, чем рассмотренные выше опыты. Поэтому можно в качестве S применить ртутную лампу без вспомогательного экрана с малым отверстием, что обеспечивает значительный световой поток. С помощью листочка слюды (толщиной 0,03 – 0,05 мм) можно получить яркую интерференционную картину прямо на потолке и на стенах аудитории. Чем тоньше пластинка, тем крупнее масштаб интерференционной картины, т.е. больше расстояние между полосами.

Полосы равного наклона

Особенно важен частный случай интерференции света, отраженного двумя поверхностями плоскопараллельной пластинки, когда точка наблюдения P находится в бесконечности, т.е. наблюдение ведется либо глазом, аккомодированным на бесконечность, либо на экране, расположенном в фокальной плоскости собирающей линзы (рис. 8.8).

В этом случае оба луча, идущие от S к P, порождены одним падающим лучом и после отражения от передней и задней поверхностей пластинки параллельны друг другу.

.

Здесь n – показатель преломления материала пластинки. Предполагается, что над пластинкой находится воздух, т.е. . Так как , (h – толщина пластинки, и – углы падения и преломления на верхней грани; ), то для разности хода получаем

.

Следует также учесть, что при отражении волны от верхней поверхности пластинки в соответствии с формулами Френеля ее фаза изменяется на π. Поэтому разность фаз δ складываемых волн в точке P равна:

,

где – длина волны в вакууме.

В соответствии с последней формулой светлые полосы расположены в местах, для которых , где m – порядок интерференции. Полоса, соответствующая данному порядку интерференции, обусловлена светом, падающим на пластинку под вполне определенным углом α. Поэтому такие полосы называют интерференционными полосами равного наклона.

Полосы равного наклона можно получить не только в отраженном свете, но и в свете, прошедшем сквозь пластинку. В этом случае один из лучей проходит прямо, а другой – после двух отражений на внутренней стороне пластинки. Однако видимость полос при этом низкая.

Для наблюдения полос равного наклона вместо плоскопараллельной пластинки удобно использовать интерферометр Майкельсона (рис. 8.9). Рассмотрим схему интерферометра Майкельсона: з1 и з2 – зеркала. Полупрозрачное зеркало посеребрено и делит луч на две части – луч 1 и 2. Луч 1, отражаясь от з1 и проходя , дает , а луч 2, отражаясь от з2 и далее от , дает . Пластинки и одинаковы по размерам. ставится для компенсации разности хода второго луча. Лучи и когерентны и интерферируют.

Интерференция от клина. Полосы равной толщины

Мы рассмотрели интерференционные опыты, в которых деление амплитуды световой волны от источника происходило в результате частичного отражения на поверхностях плоскопараллельной пластинки. Локализованные полосы при протяженном источнике можно наблюдать и в других условиях. Оказывается, что для достаточно тонкой пластинки или пленки (поверхности которой не обязательно должны быть параллельными и вообще плоскими) можно наблюдать интерференционную картину, локализованную вблизи отражающей поверхности. Возникающие при этих условиях полосы называют полосами равной толщины. В белом свете интерференционные полосы окрашены. Поэтому такое явление называют цветами тонких пленок. Его легко наблюдать на мыльных пузырях, на тонких пленках масла или бензина, плавающих на поверхности воды, на пленках окислов, возникающих на поверхности металлов при закалке, и т.п.

Рассмотрим интерференционную картину, получаемую от пластинок переменной толщины (от клина).

Направления распространения световой волны, отраженной от верхней и нижней границы клина, не совпадают. Отраженные и преломленные лучи встречаются, поэтому интерференционную картину при отражении от клина можно наблюдать и без использования линзы, если поместить экран в плоскость точек пересечения лучей (хрусталик глаза помещают в нужную плоскость).

Интерференция будет наблюдаться только во 2-й области клина, так как в 1-й области оптическая разность хода будет больше длины когерентности.

Результат интерференции в точках и экрана определяется по известной формуле , подставляя в неё толщину пленки в месте падения луча ( или ).

Поскольку разность хода лучей, отразившихся от различных участков клина, будет неодинаковой, освещенность экрана будет неравномерной, на экране будут темные и светлые полосы (или цветные при освещении белым светом, как показано на рис. 8.11). Каждая из таких полос возникает в результате отражения от участков клина с одинаковой толщиной, поэтому их называют полосами равной толщины.

На рис. 8.12 изображена оправа, в которой зажаты две стеклянные пластины. Одна из них слегка выпуклая, так что пластины касаются друг друга в какой-то точке. И в этой точке наблюдается нечто странное: вокруг нее возникают кольца. В центре они почти не окрашены, чуть дальше переливаются всеми цветами радуги, а к краю теряют насыщенность цветов, блекнут и исчезают.

Так выглядит эксперимент, в XVII веке положивший начало современной оптике. Ньютон подробно исследовал это явление, обнаружил закономерности в расположении и окраске колец, а также объяснил их на основе корпускулярной теории света.

Кольцевые полосы равной толщины, наблюдаемые в воздушном зазоре между соприкасающимися выпуклой сферической поверхностью линзы малой кривизны и плоской поверхностью стекла (рис. 8.13), называют кольцами Ньютона.

Рис. 8.12

Общий центр колец расположен в точке касания. В отраженном свете центр темный, так как при толщине воздушной прослойки, на много меньшей, чем длина волны , разность фаз интерферирующих волн обусловлена различием в условиях отражения на двух поверхностях и близка к π. . Здесь использовано условие . При наблюдении по нормали темные полосы, как уже отмечалось, соответствуют толщине , поэтому для радиуса m-го темного кольца получаем (m = 0, 1, 2, …). Если линзу постепенно отодвигать от поверхности стекла, то интерференционные кольца будут стягиваться к центру. При увеличении расстояния на картина принимает прежний вид, так как место каждого кольца будет занято кольцом следующего порядка. С помощью колец Ньютона, как и в опыте Юнга, можно сравнительно простыми средствами приближенно определить длину волны света. Полосы равной толщины можно наблюдать и с помощью интерферометра Майкельсона, если одно из зеркал з1 или з2 (рис. 8.9) отклонить на небольшой угол. Итак, полосы равного наклона получаются при освещении пластинки постоянной толщины ( ) рассеянным светом, в котором содержатся лучи разных направлений. Полосы равной толщины наблюдаются при освещении пластинки переменной толщины (клина) ( ) параллельным пучком света. Полосы равной толщины локализованы вблизи пластинки. Источник Оцените статью Вам также может понравиться Ясень семена способ распространения Ясень обыкновенный Fraxinus excelsior – так в ботанической Ярлыки способы создания ярлыков ос windows Создаем ярлыки на рабочем столе Windows Создаем ярлыки Японское удобрение фуджима способ применения Удобрения Фуджима Знаете потрясающее удобрение, палочка Японский чай способ заварки Технология заваривания японского чая Известно, что Правообладателям Политика конфиденциальности Контакты