Получение когерентных пучков делением волнового фронта
Для наблюдения интерференции света от реальных (некогерентных) источников необходимо свет от одного и того же источника разделить на два пучка (или несколько пучков) и затем свести эти пучки вместе.
Способов разделения волны от первичного источника на две когерентные между собой волны два: деление волнового фронта (метод Юнга, зеркала Френеля и др.) и деление амплитуды (интерференция в тонких пленках).
Метод получения когерентных пучков делением волнового фронта (он пригоден только для достаточно малых источников) заключается в том, что исходящий из источника пучок делится на два (например, проходя через два близкорасположенных отверстия), а при наложении их друг на друга разность хода между интерферирующими лучами должна быть меньше длины когерентности.
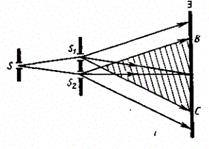
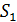
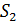
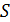
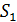
Рис. 2.2.1 Опыт Юнга
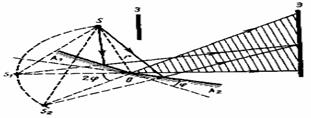
Интерференционная картина наблюдается в области взаимного перекрытия отраженных пучков.
Рис.2.2.2 Зеркала Френеля
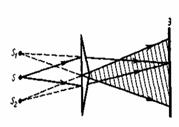
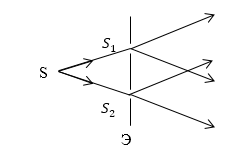
Она состоит из двух одинаковых, сложенных основаниями призм с малыми преломляющими углами. Свет от источника S преломляется в обеих призмах, в результате чего за бипризмой распространяются световые лучи, как бы исходящие из мнимых источников S1 и S2, являющихся когерентными.
Источник
Способы получения когерентных пучков делением волнового фронта
| Методы наблюдения интерференции |   |
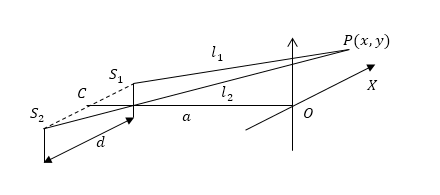
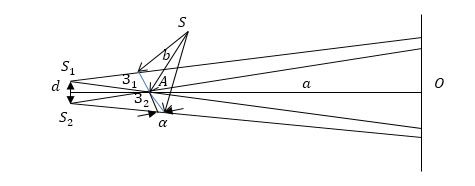
| Свет, испускаемый обычными источниками, можно рассматривать как хаотическую последовательность отдельных цугов синусоидальных волн. Длительность отдельного цуга не превышает 10 — 8 с даже в тех случаях, когда атомы источника не взаимодействуют (газоразрядные лампы низкого давления). Любой регистрирующий прибор имеет значительно большее время разрешения, поэтому наблюдение интерференции невозможно. Образование интерференционной картины можно наблюдать в рассмотренном нами в п. 8.2 опыте Юнга, использующем метод деления волнового фронта (рис. 8.3). Прошедший через узкую длинную щель S свет, вследствие дифракции образует расходящийся пучок, который падает на второй экран B с двумя, параллельными между собой узкими щелями S1 и S2, расположенными близко друг к другу на равных расстояниях от S. Эти щели действуют как вторичные синфазные источники, и исходящие от них волны, перекрываясь, создают интерференционную картину, наблюдаемую на удаленном экране C. Расстояние между соседними полосами равно: Измеряя ширину интерференционных полос, Юнг в 1802 г. впервые определил длины световых волн для разных цветов, хотя эти измерения и не были точными. Другой интерференционный опыт, аналогичный опыту Юнга, но в меньшей степени осложненный явлениями дифракции и более светосильный, был осуществлен О. Френелем в 1816 г. Две когерентные световые волны получаются в результате отражения от двух зеркал М и N, плоскости которых наклонены под небольшим углом φ друг к другу (рис. 8.4). Источником служит узкая ярко освещенная щель S, параллельная ребру между зеркалами. Отраженные от зеркал пучки падают на экран, и в той области, где они перекрываются (поле интерференции), возникает интерференционная картина. От прямого попадания лучей от источника S экран защищен ширмой В данном интерференционном опыте, также предложенном Френелем, для разделения исходной световой волны на две используют призму с углом при вершине, близким к 180°. Источником света служит ярко освещенная узкая щель S, параллельная преломляющему ребру бипризмы (рис. 8.5). Можно считать, что здесь образуются два близких мнимых изображения S1 и S2 источника S, так как каждая половина бипризмы отклоняет лучи на небольшой угол Аналогичное бипризме Френеля устройство, в котором роль когерентных источников играют действительные изображения ярко освещенной щели, получается, если собирающую линзу разрезать по диаметру и половинки немного раздвинуть (рис. 8.6). Прорезь закрывается непрозрачным экраном А, а падающие на линзу лучи проходят через действительные изображения щели Источник Получение интерференционных картин делением волнового фронта (метод Юнга) и делением амплитуды (метод Френеля)Вы будете перенаправлены на Автор24 Способов получения волн способных интерферировать в оптике всего два: деление амплитуды волны, деление фронта волны. Метод ЮнгаДля получения интерференции методом деления волнового фронта когерентные волны получают как два участка одного фронта волны. Первым, кто сконструировал установку для демонстрации явления интерференции световых волн, был Т. Юнг. При этом он использовал именно метод деления волнового фронта. Яркий пучок солнечного света попадал на экран с малым отверстием или узкой щелью. Получался как бы свет от точечного, монохроматического источника света ($S$). После дифракции на щели световая волна распространялась до двух маленьких отверстий ($S_1\ и\ S_2$), сделанных в экране ($Э$) рис.1. После очередной дифракции два расходящихся пучка света перекрывали друг друга, и так как являлись когерентными, при наложении давали интерференционную картину. При этом расстояния: Данные отверстия работают как вторичные монохроматические, точечные источники. Световые пучки вторичных источников перекрываются за экраном $Э$ (рис.1). Картина интерференции наблюдается в области перекрывания данных световых пучков. Пусть интерференционная картина наблюдается в плоскости $XOY$, перпендикулярной к нормали $CO$, проведенной к середине отрезка, соединяющего точки, в которых находятся вторичные источники света. $Ось X$ выберем параллельную отрезку $S_1S_2$ (рис.2). При этом $d$ — расстояние между отверстиями, $a$ — расстояние между отрезком $S_1S_2$ и плоскостью наблюдения. Готовые работы на аналогичную темуДля точки $P(x,y)$ (рис.2), которая находится в плоскости наблюдения, имеем: Из формул (2) и (3) следует, что: Разность путей света от источников до точки $P$ можно представить как: Интерференционная картина будет наблюдаться только в случае, если $d\ll a$. Если $x,\ y\ll a$, то: В таком случае имеем: Оптическая разность хода, следовательно, равна: При этом разность фаз имеет вид: Так как угол $S_1PS_2$ мал, то часто считают, что волны от обоих источников движутся по одному направлению, максимумы интенсивности в таком случае будут при: Так, интерференционная картина около точки $О$ (рис.2) состоит из интерференционных полос, которые лежат на одинаковых расстояниях и направлены под прямым углом к линии $S_1S_2$. Необходимо отметить, что расстояние между щелями $S_<1\ >и\ S_2$ должно быть велико в сравнении с шириной щелей. Один из способов получения щелей придумал Рэлей. Он стеклянные пластинки покрывал тонким слоем серебра, делая их непрозрачными. На серебряном слое одно пластинки лезвием бритвы делалась одна линия. На другой пластинке проводили две параллельные линии. Данные линии использовались как щели. Если применять лазеры, для опыта Юнга, то можно обойтись без первой щели. Метод ФренеляВторым способом создания интерференционной картины является метод деления амплитуды волны. Его смысл заключается в расщеплении волны света на полупрозрачной пластине на две когерентные волны. Фронт волны сохраняется, изменяется только направление его движения. Одним из методов получения когерентных источников света в данном случае, может служить устройство, которое называют зеркалами Френеля. В этом устройстве свет от точёного источника S падает на два плоских зеркала $З_1$ и $З_2$, которые расположены под небольшим углом друг к другу ($\alpha $). При отражении свет образует два мнимых когерентных источника $S_1$ и $S_2\ (рис.3).$ Плоскость $SS_1S_2$, перпендикулярна к линии пересечения зеркал, $A$ — точка пересечения. Если расстояние $SA=b$, то $S_1A=S_2A=b$. Перпендикуляр к середине отрезка $S_1S_2$ проходит через точку $А$. Расстояние между $S_1$ и $S_2$ равно: Угол $\varphi $, под которым из точки O видно расстояние $S_1S_2$, будет равен: В таком случае $\triangle x$ равно: Угол $\varphi $ можно измерить по шкале зрительной трубы. Для этого трубу размещают в точке $О$ и устанавливают ее так, чтобы отчетливо видеть изображения $S_1\ и\ S_2,\ S.\ $В таком случае легко найти длину волны $\lambda $, используя выражение: Ширина области перекрытия световых пучков равна $2a\alpha $, значит количество интерференционных полос, которые можно наблюдать ($N$) равно: В опыте Френеля интерференционная картина искажена дифракцией на ребре, по которому пересекаются зеркала. Полосы интерференции можно наблюдать на белом матовом экране или матовом стекле (на задней стороне). Задание: В опыте Юнга расстояние между щелями равно $d=0,5 мм$, длина волны света $\lambda $=0,6мкм. Ширина интерференционных полос при этом равна $\triangle x=1,2\ мм.\ $Чему равно расстояние от экрана до щелей ($a$) в данном опыте? Решение: В опыте Юнга интерференционные максимумы наблюдаются в точках, описанных выражением: Ширина первого интерференционного максимума при этом будет равна: Выразим из (1.2) искомое расстояние, получим: где для воздуха в обычных условиях $n=1$. Проведем вычисления: Ответ: $a=1м.$ Задание: В опытах с зеркалами Френеля расстояние между мнимыми источниками света равно $d,$ расстояние от них до экрана $l$. В желтом свете ширина интерференционных полос равна $\triangle x\ .\ $Какова длина волны желтого цвета? Решение: Запишем условие получения интерференционных максимумов при сложении двух когерентных волн: \[\triangle =\pm m\lambda \ \left(m=0,1,2\dots \right)\left(2.1\right),\] где $\triangle $ — оптическая разность хода волн. Она равна (рис.4): приравняем правые части выражений (2.1) и (2.2), получим: \[\frac В таком случае запишем, что: Ответ: $\lambda =\frac<\triangle xd> Источник |




 .
.
 . Для расчета освещенности J экрана можно считать, что интерферирующие волны испускаются вторичными источниками
. Для расчета освещенности J экрана можно считать, что интерферирующие волны испускаются вторичными источниками  и
и  , представляющими собой мнимые изображения щели S в зеркалах. Поэтому J будет определяться формулой двулучевой интерференции, в которой расстояние l от источников до экрана следует заменить на
, представляющими собой мнимые изображения щели S в зеркалах. Поэтому J будет определяться формулой двулучевой интерференции, в которой расстояние l от источников до экрана следует заменить на  , где
, где  — расстояние от S до ребра зеркал, b — расстояние от ребра до экрана (см. рис 8.4.). Расстояние d между вторичными источниками равно:
— расстояние от S до ребра зеркал, b — расстояние от ребра до экрана (см. рис 8.4.). Расстояние d между вторичными источниками равно:  . Поэтому ширина интерференционной полосы на экране равна:
. Поэтому ширина интерференционной полосы на экране равна: .
.
 .
.