- Способы получения когерентных пучков делением амплитуды
- Получение когерентных пучков делением амплитуды. Интерференция в тонких пленках. Полосы равного наклона и равной толщины. Кольца Ньютона.
- 10. Получение когерентных источников делением амплитуды: интерференция в тонких пленках, при отражении от тонких пластинок или кольца ньютона.
Способы получения когерентных пучков делением амплитуды
1. Полосы равной толщины.
Поверхность плоскопараллельной пластины из прозрачного материала освещается точечным источника монохроматического света. В любой точке А, распложенной на ту же сторону пластины проходят еще два луча, отраженный от верхней нижней поверхности.
Они дают нелаколизованую интерференционную картину. Рассмотрим случай, когда источник находится в бесконечности, т.е. отражается от поверхности лучи идут параллельно. Глазом, адаптируем на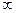 
или в фон плоскости телескопа ведем наблюдения.
Найдем оптическую разность хода. Оптическая длина – произведение геометрической длины пути луча на наклонный промежуток. Оптическая разность хода всех прошедших через линзу равен,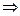 
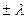
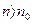
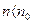
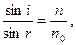
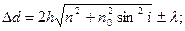
любой разности возникающей от точки М до плоскости DQ.
обусловлено потерей полудлины волны при отражении света от границ раздела оптически более плотный среды, если 
, то потери в точке М и будет «-», если 
, то в точке N и «+».
то 
(2.10)
Как следует из (2.10) при данных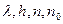 
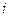
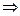
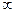
каждому наклону ( 
) лучей соответствует свои интерференционная картина полосы равного наклона. Для наблюдения следующей глаз сосредоточить на бесконечность, т.е. локализовать на 
. Если смотрим перпендикулярно к пластине.
Полосы равной толщины
Мы рассмотрели от плоскопараллельных прозрачных пластин. Теперь рассмотрим случай, когда поверхность переменной толщины. Пусть луч 1 частично отражается от поверхности плоскости прошел внутрь, отравился от нижней поверхности и попал в точку P (луч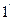 
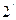
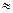
). В световом потоке, исходящем из S всегда найдется луч, который попадает в точку P часть отражается верхней поверхностью (луч 
). При определенном взаимном положении пластины и линзы лучи и 
, проходят через линзу, переходят в точку A, которая является изображением точки P. Так как и — когерентны, то в точке А будет интенсивность мала или min . если источник расположен довольно далеко и угол между поверхностями ВС и DE достаточно мал, то разность х между интенсивностью казалось будет 
равна
При достаточном удалении от поверхности источника углы падения лучей на пластину можно считать равными, в этом случае разность х будет определятся толщиной h в точке P .
что всем точкам поверхности пластины одинаковой толщины соответствует одна и та же интерференционная картина.
max и min одинаковой интенсивности соответствует точкам поверхности, в которых толщина пластины имеет одно и то же значение полос или же линии равной толщины.
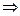
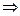
Применение интерференции
Форма интерференционной картины, положение max , min зависит от толщины и формы пластин, от угла между их поверхностями, от состояния поверхности и т.д.
Следовательно, можно, изучая форму и положение интерференционных полос, судить о свойствах исследуемой пластины, т.е. можно применить интерференционное явление для измерений физических параметров прозрачных тел.
Ценность этого метода в том, что он чувствителен к малому изменению параметров, поскольку условие свойств вещества, для которых наблюдается интерференция, имеет порядок 10 -5 см.
Рассмотрим некоторые применения интерференционных явлений.
1. Изучение соответствующей поверхности.
В оптической приближенности к поверхности оптических приборов при их изготовлении предъявляют очень высокие требования – зеркальной поверхности, поверхности линз должны быть очень гладкими.
Есть эталонная пластинка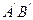 
, поверхность которой является достаточно гладкой она лежит на исследуемой АВ. Между ними существует воздушный зазор, профиль и размеры которого определяют степень и характер отклонения исследуемой поверхности от эталонной.
Если попадет на этот воздушны зазор пучок света, то лучи, отражается от нижней и верхней поверхностей, дадут соответствующую интерференционную картину.
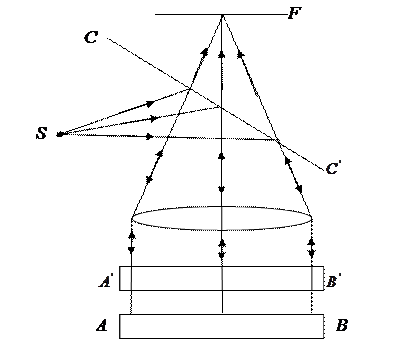
Свет от S, расположен в фокусе линзы Л, направляется на поверхность полупрозрачной пластины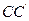 
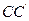
. Отражаясь от луч через линзу Л направляется на поверхность воздушного зазора. Отражающие лучи падают на экран F, расположенный в фокальной плоскости линзы, интерференционной картины. Если исследоваемая поверхность такая же гладкая, как и плоскость эталона, то в зависимости от относительного положения этих пластин будем наблюдать интенсивность полос равного наклона или равной толщины. Если же поверхность шире, то интенсивность полосы в соответствующих местах будет искривлена. По величине искривлений можно судить о размерах выступав и углублений на поверхности исследуемой пластинки.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.
Источник
Получение когерентных пучков делением амплитуды. Интерференция в тонких пленках. Полосы равного наклона и равной толщины. Кольца Ньютона.
Происхождение интерференционной картины и способ ее получения определяет вид и зависит от способа.
Рассмотрим интерферирующее устройство, представляющее собой слой прозрачного диэлектрика с частично пропускаемыми и отражаемыми поверхностями, в котором возникает геометрическая разность хода при произвольном угле падения света на это устройство.
К такому типу интерферометров относятся плоско-параллельные и клиновидные пластины (тонкие пленки, кольца ньютона) и интерферометры, расщепляющие пучки света с помощью зеркал (интерферометр Фабри-Перо)
Различают 3 вида интерференционных полос, которые получаются при следующих условиях:
1. Полосы равного наклона, которые возникают между параллельными пучками света, которые после прохождения интерферометра приобретают определенную разность хода.
< Δ=const >угол φ меняется
2. Полосы равной толщины, возникают в том случае, если интерферирующие пучки после прохождения интерферометра имеют реальное и мнимое пересечение в пространстве изображений.
φ=const> Δ меняется
3. Полосы равного хроматического порядка.
Δ =const> λ меняется
Достаточно сложные амплитудные системы, в которых требуется очень точное измерение толщины плоскопараллельной пластины или воздушных зазоров.
Рассмотрим ход луча в плоско-параллельной пластинке
Экран надо располагать в фокусе.
Δ = (AB+BC)n-AE-λ/2 – с учетом потери половины волны в точке А, так как n1=1>n2=n
Если будет выполняться противоположное условие, то потеря λ/2 будет переходить в точку B и «-λ/2» меняется на «+λ/2»
AE=AC*sinφ,sinφ=n*sinΘ> Δ=2nd*cosΘ-+ λ/2
Если на пластинку падают не параллельные пучки света, то интерферирующие пучки будут иметь все возможные направления распространения и при заданной толщине d и заданном показателе преломления n каждому углу падения φ будет соответствовать своя интерференционная картина, поэтому такие полосы будут называться полосами равного наклона.
При оксиально симметричном распространении падающих пучков, линии равного наклона являются окружностями.
Даже если источник света протяженный и различные его точки излучают не когерентно, то интерференционная картина зависит лишь от угла падения => конечность размеров источника не смазывает картину полос равного наклона.
Полосы равной величины
В световом потоке, исходящем из источника S монохроматического света всегда присутствует волна 2, интерферирующая в точке C с волной 1, прошедшей по пути SABC. Если источник расположен достаточно далеко от поверхности клина и угол между поверхностями клина достаточно мал (эти условия на практике при изучении такой схемы интерференции, как правило, выполняются), то оптическая разность хода приблизительно определяется при прочих равных условиях толщиной клина в точке C и высчитывается по той же формуле, что и для плоско-параллельной пластинки. Δ=2nd*cosΘ-+ λ/2
Однако в этом случае интерференционная картина локализована на верхней поверхности клина. Интерференционную картину можно также наблюдать и с помощью линзы на экране. В этом случае поверхность проецируется на экран наблюдения. Линии одинаковой интенсивности совпадают с линиями постоянной толщины пластины, поэтому соответствующие интерференционные полосы называются полосами равной толщины.
Примером интерференционной схемы, в которой наблюдаются полосы равной толщины, является воздушная прослойка, образованная между плоской поверхностью стекла и положенной на нее плосковыпуклой линзой (или наоборот)
В этом случае линии равной толщины – окружности, поэтому интерференционная картина имеет вид концентрических колец. Потеря полволны происходит на нижней поверхности воздушного клина.
Если h – толщина воздушного клина в точке минимума картины (темное кольцо), R – радиус кривизны линзы, то r этого 2 кольца определяются так:
считая, что h/r 2 /(2r)
Эти концентрические окружности называются кольцами Ньютона. Интерференционная картина наблюдается как в отраженном, так и в пройденном свете. Если в отраженном свете – max, то в проходящем в данной точке – min.
Интерференционная картина может наблюдаться и в белом свете (полосы будут цветными)
Все интерференционные картины, которые рассмотрены выше, соответствую двулучевой интерференции, но можно наблюдать и многолучевую интерференцию,
Источник
10. Получение когерентных источников делением амплитуды: интерференция в тонких пленках, при отражении от тонких пластинок или кольца ньютона.
Интерференцию света по методу деления амплитуды во многих отношениях наблюдать проще, чем в опытах с делением волнового фронта. Один из способов, использующих такой метод, – опыт Поля.
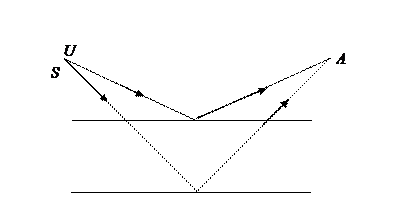
В опыте Поля свет от источника S отражается двумя поверхностями тонкой прозрачной плоскопараллельной пластинки. В любую точку P, находящуюся с той же стороны от пластинки, что и источник, приходят два луча. Эти лучи образуют интерференционную картину.
Для определения вида полос можно представить себе, что лучи выходят из мнимых изображений S1 и S2 источника S, создаваемых поверхностями пластинки. На удаленном экране, расположенном параллельно пластинке, интерференционные полосы имеют вид концентрических колец с центрами на перпендикуляре к пластинке, проходящем через источник S. Этот опыт предъявляет менее жесткие требования к размерам источника S, чем рассмотренные выше опыты. Поэтому можно в качестве S применить ртутную лампу без вспомогательного экрана с малым отверстием, что обеспечивает значительный световой поток. С помощью листочка слюды (толщиной 0,03 – 0,05 мм) можно получить яркую интерференционную картину прямо на потолке и на стенах аудитории. Чем тоньше пластинка, тем крупнее масштаб интерференционной картины, т.е. больше расстояние между полосами.
Полосы равного наклона
Особенно важен частный случай интерференции света, отраженного двумя поверхностями плоскопараллельной пластинки, когда точка наблюдения P находится в бесконечности, т.е. наблюдение ведется либо глазом, аккомодированным на бесконечность, либо на экране, расположенном в фокальной плоскости собирающей линзы (рис. 8.8).
В этом случае оба луча, идущие от S к P, порождены одним падающим лучом и после отражения от передней и задней поверхностей пластинки параллельны друг другу.
.
Здесь n – показатель преломления материала пластинки. Предполагается, что над пластинкой находится воздух, т.е. 
. Так как 
, 
(h – толщина пластинки, 
и 
– углы падения и преломления на верхней грани; 
), то для разности хода получаем
.
Следует также учесть, что при отражении волны от верхней поверхности пластинки в соответствии с формулами Френеля ее фаза изменяется на π. Поэтому разность фаз δ складываемых волн в точке P равна:
,
где 
– длина волны в вакууме.
В соответствии с последней формулой светлые полосы расположены в местах, для которых 
, где m – порядок интерференции. Полоса, соответствующая данному порядку интерференции, обусловлена светом, падающим на пластинку под вполне определенным углом α. Поэтому такие полосы называют интерференционными полосами равного наклона.
Полосы равного наклона можно получить не только в отраженном свете, но и в свете, прошедшем сквозь пластинку. В этом случае один из лучей проходит прямо, а другой – после двух отражений на внутренней стороне пластинки. Однако видимость полос при этом низкая.
Для наблюдения полос равного наклона вместо плоскопараллельной пластинки удобно использовать интерферометр Майкельсона (рис. 8.9). Рассмотрим схему интерферометра Майкельсона: з1 и з2 – зеркала. Полупрозрачное зеркало 
посеребрено и делит луч на две части – луч 1 и 2. Луч 1, отражаясь от з1 и проходя , дает 
, а луч 2, отражаясь от з2 и далее от , дает 
. Пластинки и 
одинаковы по размерам. ставится для компенсации разности хода второго луча. Лучи и когерентны и интерферируют.
Интерференция от клина. Полосы равной толщины
Мы рассмотрели интерференционные опыты, в которых деление амплитуды световой волны от источника происходило в результате частичного отражения на поверхностях плоскопараллельной пластинки. Локализованные полосы при протяженном источнике можно наблюдать и в других условиях. Оказывается, что для достаточно тонкой пластинки или пленки (поверхности которой не обязательно должны быть параллельными и вообще плоскими) можно наблюдать интерференционную картину, локализованную вблизи отражающей поверхности. Возникающие при этих условиях полосы называют полосами равной толщины. В белом свете интерференционные полосы окрашены. Поэтому такое явление называют цветами тонких пленок. Его легко наблюдать на мыльных пузырях, на тонких пленках масла или бензина, плавающих на поверхности воды, на пленках окислов, возникающих на поверхности металлов при закалке, и т.п.
Рассмотрим интерференционную картину, получаемую от пластинок переменной толщины (от клина).
Направления распространения световой волны, отраженной от верхней и нижней границы клина, не совпадают. Отраженные и преломленные лучи встречаются, поэтому интерференционную картину при отражении от клина можно наблюдать и без использования линзы, если поместить экран в плоскость точек пересечения лучей (хрусталик глаза помещают в нужную плоскость).
Интерференция будет наблюдаться только во 2-й области клина, так как в 1-й области оптическая разность хода будет больше длины когерентности.
Результат интерференции в точках и экрана определяется по известной формуле 
, подставляя в неё толщину пленки в месте падения луча ( 
или 
).
Поскольку разность хода лучей, отразившихся от различных участков клина, будет неодинаковой, освещенность экрана будет неравномерной, на экране будут темные и светлые полосы (или цветные при освещении белым светом, как показано на рис. 8.11). Каждая из таких полос возникает в результате отражения от участков клина с одинаковой толщиной, поэтому их называют полосами равной толщины.
На рис. 8.12 изображена оправа, в которой зажаты две стеклянные пластины. Одна из них слегка выпуклая, так что пластины касаются друг друга в какой-то точке. И в этой точке наблюдается нечто странное: вокруг нее возникают кольца. В центре они почти не окрашены, чуть дальше переливаются всеми цветами радуги, а к краю теряют насыщенность цветов, блекнут и исчезают.
Так выглядит эксперимент, в XVII веке положивший начало современной оптике. Ньютон подробно исследовал это явление, обнаружил закономерности в расположении и окраске колец, а также объяснил их на основе корпускулярной теории света.
Кольцевые полосы равной толщины, наблюдаемые в воздушном зазоре между соприкасающимися выпуклой сферической поверхностью линзы малой кривизны и плоской поверхностью стекла (рис. 8.13), называют кольцами Ньютона.
 Рис. 8.12 |  Общий центр колец расположен в точке касания. В отраженном свете центр темный, так как при толщине воздушной прослойки, на много меньшей, чем длина волны
Здесь использовано условие Если линзу постепенно отодвигать от поверхности стекла, то интерференционные кольца будут стягиваться к центру. При увеличении расстояния на Полосы равной толщины можно наблюдать и с помощью интерферометра Майкельсона, если одно из зеркал з1 или з2 (рис. 8.9) отклонить на небольшой угол. Итак, полосы равного наклона получаются при освещении пластинки постоянной толщины ( Источник |
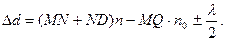
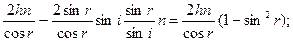
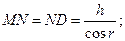
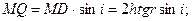
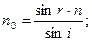
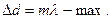
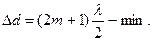
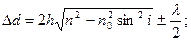
, разность фаз интерферирующих волн обусловлена различием в условиях отражения на двух поверхностях и близка к π.
.
. При наблюдении по нормали темные полосы, как уже отмечалось, соответствуют толщине 
, поэтому для радиуса 
m-го темного кольца получаем
(m = 0, 1, 2, …).
картина принимает прежний вид, так как место каждого кольца будет занято кольцом следующего порядка. С помощью колец Ньютона, как и в опыте Юнга, можно сравнительно простыми средствами приближенно определить длину волны света.
) рассеянным светом, в котором содержатся лучи разных направлений. Полосы равной толщины наблюдаются при освещении пластинки переменной толщины (клина) ( 
) параллельным пучком света. Полосы равной толщины локализованы вблизи пластинки.
