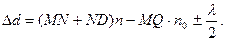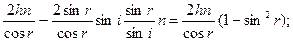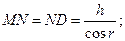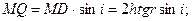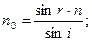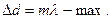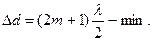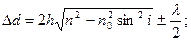Способы получения когерентных пучков делением амплитуды
1. Полосы равной толщины.
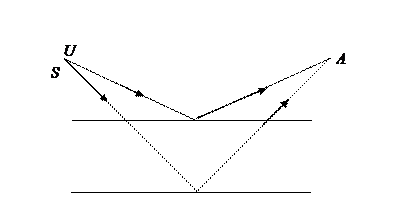
Поверхность плоскопараллельной пластины из прозрачного материала освещается точечным источника монохроматического света. В любой точке А, распложенной на ту же сторону пластины проходят еще два луча, отраженный от верхней нижней поверхности.
Они дают нелаколизованую интерференционную картину. Рассмотрим случай, когда источник находится в бесконечности, т.е. отражается от поверхности лучи идут параллельно. Глазом, адаптируем на 
или в фон плоскости телескопа ведем наблюдения.
Найдем оптическую разность хода. Оптическая длина – произведение геометрической длины пути луча на наклонный промежуток. Оптическая разность хода всех прошедших через линзу равен, 
любой разности возникающей от точки М до плоскости DQ.
обусловлено потерей полудлины волны при отражении света от границ раздела оптически более плотный среды, если 
, то потери в точке М и будет «-», если 
, то в точке N и «+».
то 
(2.10)
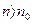
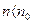
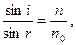
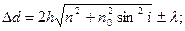
Как следует из (2.10) при данных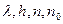 
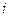
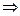
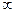
каждому наклону ( 
) лучей соответствует свои интерференционная картина полосы равного наклона. Для наблюдения следующей глаз сосредоточить на бесконечность, т.е. локализовать на 
. Если смотрим перпендикулярно к пластине.
Полосы равной толщины
Мы рассмотрели от плоскопараллельных прозрачных пластин. Теперь рассмотрим случай, когда поверхность переменной толщины. Пусть луч 1 частично отражается от поверхности плоскости прошел внутрь, отравился от нижней поверхности и попал в точку P (луч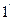 
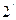
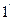
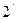
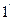
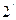
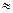
). В световом потоке, исходящем из S всегда найдется луч, который попадает в точку P часть отражается верхней поверхностью (луч 
). При определенном взаимном положении пластины и линзы лучи и 
, проходят через линзу, переходят в точку A, которая является изображением точки P. Так как и — когерентны, то в точке А будет интенсивность мала или min . если источник расположен довольно далеко и угол между поверхностями ВС и DE достаточно мал, то разность х между интенсивностью казалось будет 
равна
При достаточном удалении от поверхности источника углы падения лучей на пластину можно считать равными, в этом случае разность х будет определятся толщиной h в точке P .
что всем точкам поверхности пластины одинаковой толщины соответствует одна и та же интерференционная картина.
max и min одинаковой интенсивности соответствует точкам поверхности, в которых толщина пластины имеет одно и то же значение полос или же линии равной толщины.
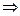
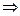
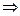
Применение интерференции
Форма интерференционной картины, положение max , min зависит от толщины и формы пластин, от угла между их поверхностями, от состояния поверхности и т.д.
Следовательно, можно, изучая форму и положение интерференционных полос, судить о свойствах исследуемой пластины, т.е. можно применить интерференционное явление для измерений физических параметров прозрачных тел.
Ценность этого метода в том, что он чувствителен к малому изменению параметров, поскольку условие свойств вещества, для которых наблюдается интерференция, имеет порядок 10 -5 см.
Рассмотрим некоторые применения интерференционных явлений.
1. Изучение соответствующей поверхности.
В оптической приближенности к поверхности оптических приборов при их изготовлении предъявляют очень высокие требования – зеркальной поверхности, поверхности линз должны быть очень гладкими.
Есть эталонная пластинка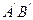 
, поверхность которой является достаточно гладкой она лежит на исследуемой АВ. Между ними существует воздушный зазор, профиль и размеры которого определяют степень и характер отклонения исследуемой поверхности от эталонной.
Если попадет на этот воздушны зазор пучок света, то лучи, отражается от нижней и верхней поверхностей, дадут соответствующую интерференционную картину.
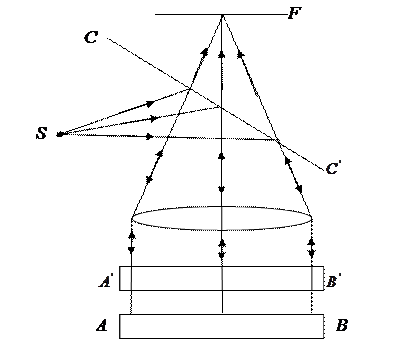
Свет от S, расположен в фокусе линзы Л, направляется на поверхность полупрозрачной пластины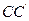 
. Отражаясь от луч через линзу Л направляется на поверхность воздушного зазора. Отражающие лучи падают на экран F, расположенный в фокальной плоскости линзы, интерференционной картины. Если исследоваемая поверхность такая же гладкая, как и плоскость эталона, то в зависимости от относительного положения этих пластин будем наблюдать интенсивность полос равного наклона или равной толщины. Если же поверхность шире, то интенсивность полосы в соответствующих местах будет искривлена. По величине искривлений можно судить о размерах выступав и углублений на поверхности исследуемой пластинки.
Источник
Получение интерференционных картин делением волнового фронта (метод Юнга) и делением амплитуды (метод Френеля)
Вы будете перенаправлены на Автор24
Способов получения волн способных интерферировать в оптике всего два:
деление амплитуды волны,
деление фронта волны.
Метод Юнга
Для получения интерференции методом деления волнового фронта когерентные волны получают как два участка одного фронта волны.
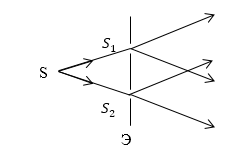
Первым, кто сконструировал установку для демонстрации явления интерференции световых волн, был Т. Юнг. При этом он использовал именно метод деления волнового фронта. Яркий пучок солнечного света попадал на экран с малым отверстием или узкой щелью. Получался как бы свет от точечного, монохроматического источника света ($S$). После дифракции на щели световая волна распространялась до двух маленьких отверстий ($S_1\ и\ S_2$), сделанных в экране ($Э$) рис.1. После очередной дифракции два расходящихся пучка света перекрывали друг друга, и так как являлись когерентными, при наложении давали интерференционную картину. При этом расстояния:
Данные отверстия работают как вторичные монохроматические, точечные источники. Световые пучки вторичных источников перекрываются за экраном $Э$ (рис.1). Картина интерференции наблюдается в области перекрывания данных световых пучков.
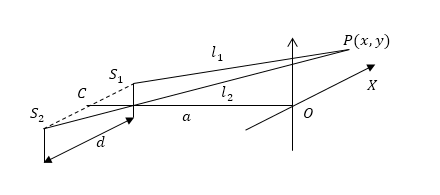
Пусть интерференционная картина наблюдается в плоскости $XOY$, перпендикулярной к нормали $CO$, проведенной к середине отрезка, соединяющего точки, в которых находятся вторичные источники света. $Ось X$ выберем параллельную отрезку $S_1S_2$ (рис.2). При этом $d$ — расстояние между отверстиями, $a$ — расстояние между отрезком $S_1S_2$ и плоскостью наблюдения.
Готовые работы на аналогичную тему
Для точки $P(x,y)$ (рис.2), которая находится в плоскости наблюдения, имеем:
Из формул (2) и (3) следует, что:
Разность путей света от источников до точки $P$ можно представить как:
Интерференционная картина будет наблюдаться только в случае, если $d\ll a$. Если $x,\ y\ll a$, то:
В таком случае имеем:
Оптическая разность хода, следовательно, равна:
При этом разность фаз имеет вид:
Так как угол $S_1PS_2$ мал, то часто считают, что волны от обоих источников движутся по одному направлению, максимумы интенсивности в таком случае будут при:
Так, интерференционная картина около точки $О$ (рис.2) состоит из интерференционных полос, которые лежат на одинаковых расстояниях и направлены под прямым углом к линии $S_1S_2$.
Необходимо отметить, что расстояние между щелями $S_<1\ >и\ S_2$ должно быть велико в сравнении с шириной щелей. Один из способов получения щелей придумал Рэлей. Он стеклянные пластинки покрывал тонким слоем серебра, делая их непрозрачными. На серебряном слое одно пластинки лезвием бритвы делалась одна линия. На другой пластинке проводили две параллельные линии. Данные линии использовались как щели.
Если применять лазеры, для опыта Юнга, то можно обойтись без первой щели.
Метод Френеля
Вторым способом создания интерференционной картины является метод деления амплитуды волны. Его смысл заключается в расщеплении волны света на полупрозрачной пластине на две когерентные волны. Фронт волны сохраняется, изменяется только направление его движения.
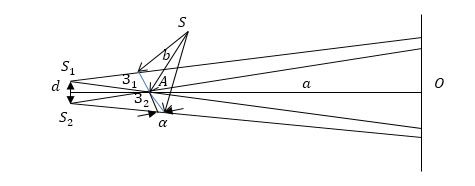
Одним из методов получения когерентных источников света в данном случае, может служить устройство, которое называют зеркалами Френеля. В этом устройстве свет от точёного источника S падает на два плоских зеркала $З_1$ и $З_2$, которые расположены под небольшим углом друг к другу ($\alpha $). При отражении свет образует два мнимых когерентных источника $S_1$ и $S_2\ (рис.3).$ Плоскость $SS_1S_2$, перпендикулярна к линии пересечения зеркал, $A$ — точка пересечения. Если расстояние $SA=b$, то $S_1A=S_2A=b$. Перпендикуляр к середине отрезка $S_1S_2$ проходит через точку $А$. Расстояние между $S_1$ и $S_2$ равно:
Угол $\varphi $, под которым из точки O видно расстояние $S_1S_2$, будет равен:
В таком случае $\triangle x$ равно:
Угол $\varphi $ можно измерить по шкале зрительной трубы. Для этого трубу размещают в точке $О$ и устанавливают ее так, чтобы отчетливо видеть изображения $S_1\ и\ S_2,\ S.\ $В таком случае легко найти длину волны $\lambda $, используя выражение:
Ширина области перекрытия световых пучков равна $2a\alpha $, значит количество интерференционных полос, которые можно наблюдать ($N$) равно:
В опыте Френеля интерференционная картина искажена дифракцией на ребре, по которому пересекаются зеркала. Полосы интерференции можно наблюдать на белом матовом экране или матовом стекле (на задней стороне).
Задание: В опыте Юнга расстояние между щелями равно $d=0,5 мм$, длина волны света $\lambda $=0,6мкм. Ширина интерференционных полос при этом равна $\triangle x=1,2\ мм.\ $Чему равно расстояние от экрана до щелей ($a$) в данном опыте?
Решение:
В опыте Юнга интерференционные максимумы наблюдаются в точках, описанных выражением:
Ширина первого интерференционного максимума при этом будет равна:
Выразим из (1.2) искомое расстояние, получим:
где для воздуха в обычных условиях $n=1$. Проведем вычисления:
Ответ: $a=1м.$
Задание: В опытах с зеркалами Френеля расстояние между мнимыми источниками света равно $d,$ расстояние от них до экрана $l$. В желтом свете ширина интерференционных полос равна $\triangle x\ .\ $Какова длина волны желтого цвета?
Решение:
Запишем условие получения интерференционных максимумов при сложении двух когерентных волн:
\[\triangle =\pm m\lambda \ \left(m=0,1,2\dots \right)\left(2.1\right),\]
где $\triangle $ — оптическая разность хода волн. Она равна (рис.4):
приравняем правые части выражений (2.1) и (2.2), получим:
\[\frac
В таком случае запишем, что:
Ответ: $\lambda =\frac<\triangle xd>
Источник
