Модели поиска



Совокупность признаков, на основании которых определяется релевантность документов по отношению к информационному запросу и принимается решение о выдаче или невыдаче данного документа в ответ на поставленный информационный запрос, как уже говорилось, называется критерием выдачи или критерием смыслового соответствия (КСС).
Критерии в совокупности с методами их реализации называют моделями поиска. Здесь под моделью будем понимать логическую или математическую модель, в рамках и терминах которой и формулируется КСС. Принятая модель поиска определяет многие компоненты ИПС и их взаимодействие, в первую очередь, индексирование документов и запросов и тем самым структуру ПОД и ПОЗ, собственно критерий и тем самым результаты поиска. Поисковые образы являются результатом применения некоторой модели информационного массива документов, ориентированной на поиск, к реальному массиву. Алгоритмы сравнения ПОД и ПОЗ реализуют правила вычисления релевантности документа и запроса в соответствии с выбранной моделью. В идеале модели поиска должны включать в себя также и модель пользователя: формализованное описание и обработку при поиске пользователя, типа запроса, целей поиска и т.д.
Модели поиска информации можно охарактеризовать четырьмя параметрами:
представлением документов и запросов;
методами сопоставления, применяемыми для оценки релевантности документа запросу пользователя;
методами ранжирования результатов запроса;
механизмами обратной связи, обеспечивающими оценку релевантности пользователем.
Можно утверждать, что главными здесь являются методы сопоставления оценки релевантности ПОД и ПОЗ, которые определяют остальные параметры.
Существует несколько типов моделей поиска информации: теоретико-множественные, логические, векторные (алгебраические), вероятностные и гибридные.
Теоретико-множественные модели являются самыми простыми и основываются на количественном КСС, в частности, на теоретико-множественной операции пересечения множеств терминов ПОД и ПОЗ. Степень такого пересечения выражает степень релевантности документов и запросов.
Наиболее популярной моделью является булева, или логическая, модель, которая трактует термины в запросе как булевы переменные. При наличии термина в документе соответствующая переменная принимает значение «true» (истина). Присваивание терминам весовых коэффициентов не допускается. Запросы формулируются как произвольные булевы выражения, связывающие термины с помощью стандартных логических операций: AND, OR или NOT. Мерой соответствия запроса документу служит значение статуса выборки (RSV, retrieval status value). В булевой модели статус выборки равен либо 1, если для данного документа вычисление выражения запроса дает значение «истина», либо 0 в противном случае. Все документы с RSV = 1 считаются релевантными запросу.
Такая модель проста в реализации и применяется во многих системах. Она позволяет пользователям вводить в свои запросы произвольно сложные выражения, однако эффективность поиска зависит от умения и опыта пользователя и обычно невысока. К тому же ранжировать результаты невозможно, так как все найденные документы имеют одинаковые RSV, а терминам нельзя присвоить весовые коэффициенты. Нередко результаты выглядят не очень естественно. Например, если пользователь указал в запросе десять терминов, связанных логической операцией AND, документ, содержащий девять таких терминов, в выборку не попадет. Для повышения эффективности поиска в таких ИПС рекомендуется применять обратную связь с пользователем. Неадекватность собственно логического критерия смыслового соответствия была показана давно. Однако на практике до сих пор превалируют системы с булевой логикой.
Модель, основанная на нечеткой логике (или нечетких множествах),допускает (в отличие от обычной логики и теории множеств) частичную принадлежность элемента тому или иному множеству. Здесь логические операции переопределены таким образом, чтобы учесть возможность неполной принадлежности множеству, и это роднит ее с вероятностными моделями, а обработка запросов пользователя выполняется аналогично булевой модели, но результат вычисления истинности логических операций принимает значения в диапазоне [0,1].

Строгая булева модель и модель, использующая методы теории нечетких множеств, требуют меньших объемов вычислений (при индексировании и оценке соответствия документов запросу), чем другие модели. Они менее сложны алгоритмически и предъявляют не очень жесткие требования к другим ресурсам, таким как дисковое пространство для хранения представлений документов.
Векторная модель (другие названия – пространственно-векторная, алгебраическая, линейная) основана на предположении, что совокупность документов можно представить набором векторов в пространстве, определяемом базисом, из n нормализованных векторов-терминов. Если быть более точным, то документу приписывается вектор размерности, равный числу терминов, которыми можно воспользоваться при индексировании (поиске). В пространстве, натянутом на n нормализованных векторов, каждый документ будет представлен n-мерным вектором. При простой векторной модели элемент вектора равен 1 или 0, в зависимости от наличия или отсутствия термина в ПОД. В более сложных моделях термины взвешиваются – элемент вектора равен не 1 или 0, а некоторому числу (весу), отражающему вес термина в документе. Запрос пользователя также представляется n-мерным вектором. Показатель RSV, определяющий соответствие документа запросу, задается скалярным произведением векторов запроса и документа. Чем больше RSV, тем выше релевантность документа запросу.
Достоинство подобной модели в ее эффективности и простоте. Она позволяет взвешивать термины, ранжировать результаты поиска по релевантности, реализовать обратную связь для оценки релевантности пользователем. В то же время приходится жертвовать выразительностью спецификации запроса, присущей булевой модели. Именно последняя модель в различных модификациях стала наиболее популярной в ИПС сети Интернет.
Наиболее сложной и перспективной считается вероятностная модель. Данная модель базируется на вероятности релевантности и нерелевантности документа запросу пользователя, которые вычисляются на основе вероятностных весовых коэффициентов терминов и фактического присутствия терминов в документе. Кроме того, в этой модели применяются два стоимостных параметра. Они характеризуют соответственно потери, связанные с включением в результат нерелевантного документа, и пропуском релевантного документа. Данная модель требует определения вероятностей вхождения термина в релевантные и нерелевантные части совокупности документов, оценить которые довольно сложно. Между тем она выполняет важную функцию, объясняя процесс поиска и предлагая теоретическое обоснование методов, применявшихся ранее эмпирически. Теоретические подходы были сформулированы давно, но практического применения не нашли в силу своей сложности.
Существуют разные вероятностные модели документального поиска. В одних критерии, влияющие на оценку релевантности, являются свойствами потребителя (запроса). Поэтому история, статистика предыдущих поисков здесь оказывается чрезвычайно полезной.
Другой тип вероятностных моделей интерпретирует поисковую ситуацию следующим образом. Имеется массив документов, обладающих различными свойствами: семантическим значением (здесь мы имеем в виду значение в информационно-поисковом понимании: как предметное содержание), лингвистическими характеристиками (лексических единиц), библиографическими характеристиками и т.п. Запрос пользователя выражает информационную потребность в терминах этих свойств. Формальное обнаружение этих поисковых признаков говорит не о релевантности документа и запроса, а только о вероятности, что документ может быть оценен «хозяином» запроса как релевантный.
На практике в реальных информационно-поисковых системах часто применяются гибридные модели, которые совмещают в себе свойства и функции нескольких моделей.
Источник
3 Модели поиска информации
Главная цель ИПС – наилучшим образом удовлетворить потребности пользователей в необходимой информации. Для реализации этой глобальной цели необходимо проделать ряд подготовительных операций, которые были подробно рассмотрены в первой части лекций: проанализировать информационный массив и представить его в форме, удобной для хранения и обработки.
Не менее важной частью поискового аппарата ИПС является модель поиска информации. Она описывает способ и критерии сравнения запросов и документов, а также форму представления результатов этого сравнения.
Любая модель поиска тесно связана с информационно-поисковым языком. Информационно-поисковый язык(ИПЯ) – это специальный язык для формирования запросов к ИПС. Необходимость создания ИПЯ вызвана трудностями интерпретации естественного языка в компьютерной системе. Однако синтаксис информационно-поисковых языков обычно довольно прост и внешне они часто похожи на естественные.
Перед использованием запросов на ИПЯ проводятся лексическая обработказапроса (например, удаление из запроса терминов, присутствующих в стоп-словаре),морфологическая обработка(нормализация терминов запроса), режесинтаксическая и семантическая обработки(в основном в экспериментальных системах) . В базе данных ИПС термины обычно хранятся в так называемой нормальной форме. Например, для существительных — это именительный падеж единственного числа. Одновременная нормализация терминов запросов и документов позволяет существенно упростить процесс их сравнения при поиске.
Рассмотрим основные модели поиска информации, применяемые в ИПС.
3.1 Булева модель поиска
Наиболее распространенной моделью поиска является булева модель, позволяющая составлять логические выражения из набора терминов. Найденные документы определяются в результате описанных запросом логических операций над множеством поисковых образов документов. Пользователь получает только те документы, чьи наборы терминов точно совпадают с соответствующими комбинациями терминов запроса.
Поисковые образы запросов связывают термины с помощью булевых операторов(«И» – «AND», «ИЛИ» – «OR», «И НЕ» – «AND NOT»). Эти операции производятся над множествами документов, содержащих тот или иной термин, определенный запросом.
Для обозначения объединения множеств («ИЛИ» в запросе) применяется символ 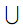
Например, оператор «И», соединяющий два термина запроса, означает следующее. Из множества всех документов нужно сначала выбрать два подмножества.
Одно из них содержит первый термин запроса, а другое – второй. Затем определяется общая часть (пересечение) этих подмножеств, то есть те документы, в состав которых одновременно входят и первый, и второй термины из запроса.
Рассмотрим, например, такой запрос:
(((Microsoft and Word) or (Microsoft and Excel)) and Macintosh) and not Windows
В данном случае выражение на ИПЯ означает следующее:
нужно найти все документы, которые одновременно содержат либо сочетание «Microsoft Word», либо сочетание «Microsoft Excel», а также содержат слово «Macintosh», но не содержат слово «Windows».
Этот запросможно разбить на две части:
1. Microsoft and Word and Macintosh and not Windows
2. Microsoft and Excel and Macintosh and not Windows
Выполнение первого запросапроисходит в два этапа. Сначала находятся все документы, содержащие термины «Microsoft», «Word» и «Macintosh». Затем из найденных документов отсеиваются те, которые содержат слово «Windows».
Второй запросвыполняется аналогично. В конце производится объединение результатов работы первой и второй частей исходного запроса.
Часто пользователь строит свой запрос, не используя каких-либо логических операторов, и просто перечисляет ключевые слова. В таком случае обычно предполагается, что все термины соединены логической операцией «И».
В некоторых поисковых системах вместо булевых операторов язык запросов позволяет использовать различные знаки. Так, знак «+» эквивалентен оператору «И», знак «-» – оператору «И-НЕ» и т. д.
В процессе поиска из исходного информационного массива выделяется часть, которая содержит найденные документы, соответствующие комбинациям терминов запроса. Какого-либо упорядочения (например, ранжирования по релевантности) не проводится: все выданные документы считаются одинаково важными.
Несколько типичных булевых стратегий поиска изображено в табл.1.
Здесь e d c b a , , , ,– термины, из которых состоят запросы, а E D C B A , , , ,– множества документов, содержащих эти термины (например, A — это множество документов, содержащих термин a , и т. д.).
ИПС, работающие с булевой моделью поиска, имеют ряд недостатков.
1.Обычные булевы запросы затрудняют варьирование глубины поиска с целью выдачи большего или меньшего количества документов в зависимости от требований пользователя. Для получения желаемого уровня эффективности необходимо найти правильную формулировку запроса: не слишком широкую и не слишком узкую.
Оператор AND может привести к резкому сокращению числа найденных документов, а оператор OR, напротив, может чрезмерно расширить запрос и выделить нужную информацию из информационного шума будет трудно. Результат поиска также сильно зависит от того, насколько типичными для базы данных ключевых слов являются термины запроса. Поэтому для успешного применения булевой модели следует хорошо ориентироваться в предметной лексике. Для повышения результативности создаются специальные словари — тезаурусы, которые содержат информацию о связи терминов друг с другом.
2.При использовании булевой логики нельзя получить эффект от функций совпадения векторов, которые дают непрерывный спектр совпадений (полных, частичных или нулевых) между запросами поисковыми образами документов. Это обстоятельство приводит к жесткому требованию «все или ничего» на выходе.
3.Еще одним минусом является тот факт, что множество выданных документов не может быть представлено пользователю в ранжированном виде (ранжирование – упорядочение результатов поиска по некоторому критерию соответствия их информационной потребности пользователя), например в порядке уменьшения сходства между документом и запросом. Документ либо полностью соответствует запросу, либо не соответствует совсем. Эта проблема может быть решена с помощью взвешенного булева поиска, при котором производится частичное ранжирование с использованием весов терминовWi . Результаты поиска располагаются в порядке уменьшения весов совпавших терминов [, , ].
Несмотря на описанные недостатки, булева модель поиска широко применяется в современных ИПС из-за простоты ее реализации.
Источник