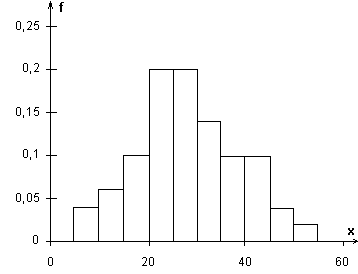Способы первичного описания данных

Способы первичного описания данных. Протоколирование данных

Первичная обработка данных:

1. Составление таблиц.В большинстве случаев обработку начинают с составления таблиц (сводных таблиц) полученных данных. В таблицу можно свести не только числовые данные. К данным качественного хар-ра также могут быть применены простейшие способы количественной обработки. Для всей выборки и отдельных подборок могут быть подсчитаны частоты встречаемости , а затем и частости интересующих вас индикаторов, проявлений некоторого вида.

Основной формой таблицы явл. следующая. По строкам занесены значения показателей каждого испытуемого — в одной строке значения показателей одного испытуемого. По столбцам расположены значения каждого заносимого в таблицу признака — в одном столбце находятся значения одного признака по всем испытуемым. Все строки и все столбцы должны быть пронумерованы. Последовательность признаков может быть упорядочена по разным основаниям.

В первых столбцах лучше разместить демографические, социо-демографические показатели: пол, возраст, уровень образования и т.д. Затем по убывающей значимости (уровню информативности) измеренные параметры. Параметры, полученные с помощью одной методики, удобней располагать компактно — в одной группе. Испытуемые могут быть расположены по алфавитному порядку их фамилий, по лучше использовать этот принцип на самом нижнем уровне деления. Форма сводной таблицы данных.

№

Сидоров

Петров

Иванов

Среднее

В исходную сводную таблицу чаще всего заносят сырые данные. Сейчас преимущественной формой математико-статистической обработки стала компьютерная технология. Если форма распределения эмпирических данных незначительно отличается от нормального распределения, то предварительное центрирование, нормирование или перевод в шкальные оценки по имеющимся в данной методике таблицам не требуется. Для начала можно предположить, что выбранный вами метод подходит для обработки средствами параметрической статистики.

2. Преобразование формы информации.В таблицу целесообразно внести все интересующие вас признаки в форме десятичного числа. Т.е., предварительно пересчитать минуты в десятичную часть часа, секунды в десятич. часть минуты, количество месяцев в десятичную часть года. В виде чисел в таблицу можно вписать информацию и о тех параметрах выборки, кот. предположительно могут оказаться значимыми факторами, но имеются у вас в качественных показателях. Наиболее простыми операциями могут быть: числовое кодирование (муж. — 2, женщ. — 1; прошедшие обучение — 2, непрошедшие — 1 и т.д.) и перевод качественных показателей в ранги. Число 0 для кодирования лучше не использовать, поскольку некоторые статистические компьютерные программы не смогут обработать такие данные. Это не значит, что в таблицу вообще не могут быть записаны нулевые значения. Уровень образования можно ранжировать таким образом:

Ранг Уровень образования:

1 — закончены менее 5 классов школы;

2 — закончены 5-8 классов или училище с дипломом о неполном среднем образовании;

3 — закончены 9-11 классов или училище с дипломом о полном среднем образовании;

4 — закончены техникум или колледж, или 1 -2 курса вуза;

5 — закончены 3-6 курсов вуза без диплома о высшем образовании;

6 — закончен вуз с дипломом;

7 — закончены аспирантура или адъюнктура, или ординатура, или другие формы пост дипломного образования со сроком обучения 2 года и более.

studopedia.org — Студопедия.Орг — 2014-2021 год. Студопедия не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования (0.002 с) .

Источник

Методы первичного описания данных

Тема 3 Первичное описание исходных данных

Для первичного описания исходных данных чаще всего используются таблицы, вариационные ряды и графики. Частным случаем таблицы является таблица кросс-табуляции. Таблицы кросс-табуляции используются для анализа номинативных данных и указывают частоту встречаемости явления. Например, приведенная ниже таблица 2 х 2 демонстрирует наличие или отсутствие интереса к математике у студентов факультета психологии СПбАА обоих полов.

М	Ж
Наличие интереса
Отсутствие интереса
Всего:

Можно ли сказать, что у студентов-юношей интерес к математике выражен меньше, чем у студентов-девушек? Для ответа на данный вопрос следует использовать специальные статистические методы, например, критерий χ 2 (читается «хи–квадрат»). Работе с указанным критерием будет посвящен специальный раздел пособия.

Вариационый ряд – упорядоченное отражение распределение значений признака, представляющий двойной ряд чисел и состоящий из обозначения классов и соответствующих частот. В строке признаков можно использовать не только градации (степень выраженности), но и метрические данные, и диапазоны метрических данных.

Степень экстра- версии

Частота (кол-во случаев)

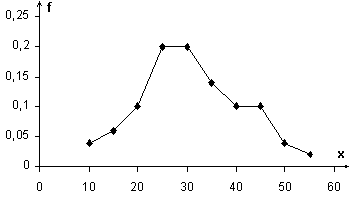
Графики (называются также диаграммами) – это чертежи, которые можно использовать для наглядности распределения количественно выраженной величины в выборке. При этом по оси ординат всегда откладывается частота. Ниже дан пример одного из видов графиков, называемого полигоном (представляет собой ломаную линию), демонстрирующего распределение показателей экстраверсии.

Среди графиков также часто используются гистограммы распределения. Они представляют собой столбиковые диаграммы, при этом каждый столбец опирается на значение признака (интервал значения) переменной. Высота столбца соответствует частоте встречаемости этого значения. Ниже приведен пример гистограммы (значения те же).

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Первичное описание исходных данных

Метрические данные можно представить в виде ряда значений, называемого статистической совокупностью (массивом). Каждый член этой совокупности, в свою очередь называется вариантой. Массив заключается в фигурные скобки. Если среди вариант есть десятичные дроби, то варианты должны разделяться между собой точкой с запятой. Если все варианты – целые числа, их можно разделять запятыми. Массивы бывают упорядоченные и неупорядоченные.

Также для первичного описания исходных данных используются таблицы, вариационные ряды и графики.

Результаты исследования репрезентативной выборки можно подвергать анализу с использованием математических методов. Для этого необходимо специальное оформление (представление) результатов опыта. Наиболее востребованным и часто применяемым является метод представления результатов опыта в виде вариационного ряда.

Вариационный ряд –это таблица, отображающая зависимость между видами исходов проводимого опыта и количествами тех или иных исходов.

Рассмотрим следующий эксперимент. Тридцати студентам был задан следующий вопрос: «Какое чувство наиболее ярко проявляется (ощущается) Вами в момент сдачи важного экзамена?» В результате вопроса были получены такие варианты ответов: «страх», «подавленность», «волнение», «растерянность», «ничего не чувствую», «эмоциональное возбуждение». Т.е. в данном эксперименте опытом является опрос. Разновидности исхода опыта – это различные ответы испытуемых. Чтобы составить вариационный ряд, необходимо знать, сколько человек дали тот или иной ответ. Если «страх» испытывают 5 человек, «подавленность» — 2 человека, «волнение» — 14 человек, «растерянность» — 4 человека, «ничего не чувствуют» — 2 человека, а «эмоциональную возбуждение» — 3 человека, то искомая таблица будет выглядеть следующим образом:

Исход опыта	Страх	Подав-ленность	Волнение	Расте-рянность	Ничего не чувствуют	Эмоци-ональное возбуждение
Количество исходов

Построенная таблица отражает результаты проделанного опыта. При этом для математической обработки результата, как правило, необходимо представить исходы опыта в числовом виде. Например, испытываемые чувства можно пронумеровать и в таблице вместо их словесной формулировки записать соответствующие номера.

В некоторых исследованиях исходы опыта выражаются числами, а значит, искусственное числовое представление вариантов не требуется.

В классе провели тестирование по определению уровня доверия учащихся друг к другу. Уровень доверия определяется по 10-балльной шкале. Результатом исследования стали следующие данные: уровень доверия, равный 1, определился у 1 человека, равный 2 – у 3 человек, равный 4 – у 6 человек, равный 6 – у 9 человек, равный 8 – у 4 человек, равный 10 – у 2 человек.

Запишем полученные результаты в виде вариационного ряда, где имеют место следующие варианты: 1, 2, 4, 6, 8 и 10 баллов. Получим следующую таблицу:

Вариант

Количество испытуемых

Для удобства при использовании математических методов исследования элементы множества значений выборки (варианты исхода опыта) обозначают через x_i. В рассматриваемом примере их можно обозначить: x₁=1, x₂=2, x₃=4, x₄=6, x₅=8, x₆=10. Количества испытуемых, соответствующих тому или иному варианту, называют частотами данных вариантов. Обычно частоты обозначаются через n_i. Например, для варианта x₃=4 частота n₃ равна 6. При этом общее количество испытуемых, принявших участие в исследовании, называется объёмом выборки, который находится как сумма всех частот и обозначается буквой n. В данном случае n=1+3+6+9+4+2=25.

Для того чтобы показать, какую долю от всего объёма выборки представляет тот или иной вариант, используется понятие относительной частоты.

Относительные частоты обозначаются через f_i и определяются как отношение соответствующей частоты n_i к объёму выборки n, т.е. f_i = n_i/n.

Таблица, отображающая зависимость между вариантами x_i и относительными частотами f_i называется статистическим рядом.

Важно заметить, что в вариационном и статистическом рядах варианты принято располагать в порядке возрастания. Сумма относительных частот статистического ряда всегда равна единице: 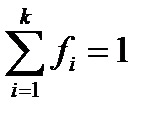, где k – количество различных вариантов.

Составим статистический ряд для рассмотренного опыта с изучением уровня доверия школьников друг к другу.

Для решения поставленной задачи достаточно разделить соответствующие значения частот на объём выборки n=25. Например, f₁ = n₁/n=1/25=0.04; f₂ = n₂/n=3/25=0,12. и т.д. В результате получим следующий статистический ряд:

Вариант xi
Относительная частота fi	0.04	0.12	0.24	0.36	0.16	0.08

Убедимся, что .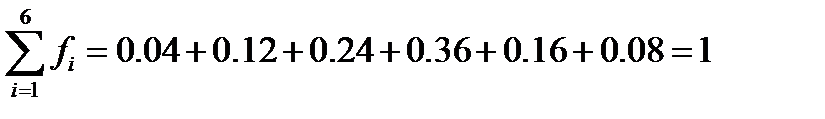

Иногда для лучшей иллюстрации результатов исследования используют полигон частот.

Под полигоном частот выборкипонимают ломаную линию с вершинами в точках (x_i; m_i). Используют также полигон относительных частот выборки, для которого вершины ломаной имеют координаты (x_i; f_i).

Построим полигон относительных частот для изучения уровня тревожности (по 100-балльной шкале), по следующим результатам:

xi (Тревожность, баллы)

ni (Количество испытуемых, чел.)

Найдём сначала объём выборки: n=2+3+5+10+10+7+5+5+2+1=50. Далее построим статистический ряд. Для этого найдём относительные частоты f_i = n_i/n.

xi (Тревожность)
fi (Относительная частота)	0.04	0.06	0.1	0.2	0.2	0.14	0.1	0.1	0.04	0.02

Теперь можно построить полигон относительных частот.

Помимо полигона частот для иллюстрации результатов опыта используются также столбчатые и круговые диаграммы.

Столбчатая диаграмма строится аналогично полигону частот. Отличие заключается в том, что вместо отрезков изображаются прямоугольники соответствующей высоты.

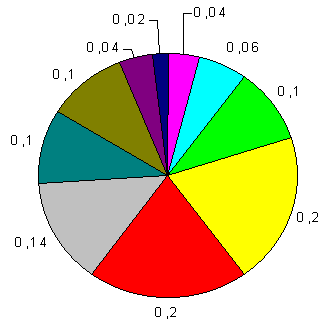
На круговой диаграмме вариант отображается в виде сектора, градусная мера угла которого равна 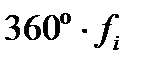. Рассчитаем градусные меры секторов, соответствующих тем или иным частотам:

xi (Тревожность)
fi (Относительная частота)	0.04	0.06	0.1	0.2	0.2	0.14	0.1	0.1	0.04	0.02
Градусная мера сектора	14.4	21.6	50.4	14.4	7.2

Таким образом, круговая диаграмма будет иметь вид:

Помимо диаграмм для наглядного представления результатов, а также для установления аналога с классическим законом распределения, используется гистограмма, для чего вводится понятие плотности относительной частоты.

Плотность относительной частоты равна отношению суммы частот соответствующего интервала к произведению общего объёма выборки n и длины h_i соответствующего интервала. Т.е. плотность относительной частоты вычисляется следующим образом: n_i/(n*h_i).

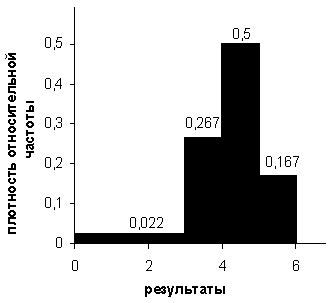
Пусть результаты теста записаны в таблице:

Результат теста (в баллах) (интервалы)	Количество испытуемых (чел.), ni	Плотность относительной частоты
Менее 3 баллов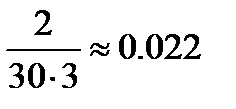
От 3 до 4 баллов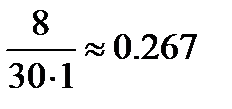
От 4 до 5 баллов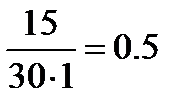
От 5 до 6 баллов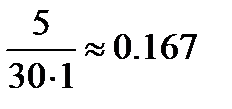

Построим гистограмму результатов тестирования, для чего потребуется нахождение плотности относительной частоты. Она рассчитывается следующим образом. Сначала необходимо узнать объём n всей выборки, т.е. количество участников тестирования.

Для каждого интервала находим его длину h_i:

Для построения гистограммы выборки воспользуемся прямоугольной декартовой системой координат. По оси абсцисс отметим имеющиеся интервалы: от 0 до 3, от 3 до 4, от 4до 5 и от 5 до 6. Сопоставим каждой абсциссе из выбранного интервала ординату, равную соответствующей плотности относительной частоты (см. рисунок). В качестве графика получим отрезки, параллельные оси абсцисс. Для наглядности эти отрезки можно достроить до закрашенных прямоугольников. При этом площадь каждого полученного прямоугольника будет численно равна соответствующей относительной частоте. Поэтому вся площадь закрашенной фигуры будет равна единице. Таким образом, мы получим графическое отображение относительных частот выборки.

При построении гистограммы мы опирались на данные, записанные в таблице с помощью интервального метода. Если выборка имеет сравнительно большой объём или содержит большое количество различных вариантов, то могут возникнуть трудности вычислительного характера. Для решения этой проблемы и применяется метод интервалов.

Суть метода интервалов заключается в разбиении множества значений измеряемой величины на интервалы. Тогда выборка записывается следующим образом:

Измеряемая величина xi			…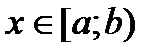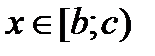
Частота ni	n1	n2	…

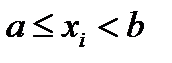
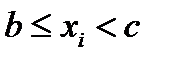
Такая запись означает, что выборка содержит n₁ значений величины x_i таких, что , n₂ значений величины x_i таких, что . Выборку можно представить в виде любого количества интервалов.

Подытоживая сказанное, заметим, что для организации педагогических исследований с помощью математических методов изначально полученную в результате опыта информацию необходимо представить в виде вариационного или статистического ряда. Для наглядности вариационный и статистический ряды изображаются при помощи диаграмм, полигонов частот или гистограмм.

Зная, как можно представить результаты эксперимента для их математической обработки, целесообразно перейти непосредственно к рассмотрению математических методов.

Источник