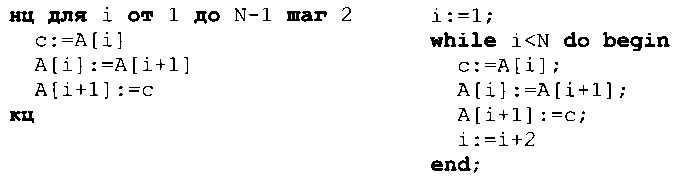Способы перестановки элементов массива

Одномерные массивы

Тема: Перестановка элементов массива.

Перестановка двух элементов

Задача. Поменять местами два элемента массива с номерами k1 и k2.

Рассмотрите процедуру, с помощью которой эта задача легко решается.

Procedure Obmen2(Var m : MyArray; n, k1, k2 : integer;); Var x : integer; Begin x:=m[k1]; m[k1] := m[k2]; m[k2] := x; End;

Перестановка части массива

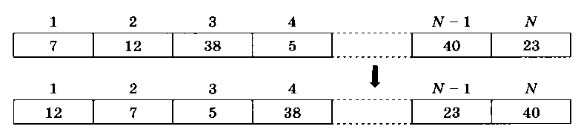
Задача. Дан одномерный массив А, состоящий из 2n элементов. Поменять местами первую и вторую его половины

Задание. Оформите решение этой задачи, применив процедуру обмена значений Obmen2, рассмотренную выше.

Заметим лишь, что Вы должны поменять местами элементы с номерами 1 и n+1, 2 и n+2 и т.д., последняя пара — n и 2n, а значит, обмен происходит по правилу: элемент с номером i меняется местами с элементом с номером n+i. Эту закономерность следует применить в организации обращения к процедуре обмена. Например, так

for i := 1 to n do Obmen2(A, 2*n, i, i+n,);

Задание. Выберите с учителем задачи для самостоятельного решения из предложенного списка:

Поменять местами:
а) первый элемент и максимальный;
б) второй и минимальный;
в) первый и последний из отрицательных чисел.

Дан одномерный массив А, состоящий из 2n элементов. Поменять его половины следующим образом: первый элемент поменять с последним, второй с предпоследним и так далее.

Дан одномерный массив В, состоящий из 2n элементов. Переставить его элементы по следующему правилу:
а) b[n+1], b[n+2], . b[2n],b[1], b[2], . b[n];
b) b[n+1], b[n+2], . b[2n],b[n], b[n-1], . b[1];
c) b[1], b[n+1],b[2], b[n+2], . b[n], b[2n];
d) b[2n], b[2n-1], . b[n+1],b[1], b[2], . b[n];

Дан одномерный массив. Переставить в обратном порядке элементы массива, расположенные между минимальным и максимальным элементами.

Работа с несколькими массивами

В Turbo Pascal можно одним оператором присваивания передать все элементы какого-либо массива другому массиву того же типа, например:

Var a, b: array [1 .. 5] of integer; Begin . a:=b; . End.

После такого присваивания все пять элементов массива a получат значения из массива b.

Рассмотрим одну из типичных задач.

Задача. Найти скалярное произведение двух массивов.

Скалярным произведением двух массивов одинаковой размерности называется сумма произведений соответствующих элементов. Это можно записать так:

где n — это количество элементов в массивах (размерность).

Тогда можно составить следующую функцию:

Function Sp (a, b : MyArray; n ; integer) : LongInt; Var i : Integer; s : LongInt; Begin s:= 0; for i := 1 to n do s := s+a[i]*b[i]; Sp := s; End;

Задание. Выберите с учителем задачи для самостоятельного решения:

Дан одномерный массив чисел а. Cформируйте такой массив b, который содержит копию положительных элементов массива а.

Скопируйте отрицательные и положительные кратные заданному числу элементы массива А в массив В в обратном порядке.

Из двух упорядоченных одномерных массивов (длины K и N) сформируйте одномерный массив размером K+N, упорядоченный так же, как исходные массивы.

Из двух упорядоченных одномерных массивов (длины K и N) сформируйте одномерный массив размером K+N, упорядоченный в обратную сторону.

Дан упорядоченный целочисленный массив. Сформировать второй массив всех таких различных значений, которые в первом массиве встречаются по два и более раза.

Дан упорядоченный целочисленный массив. Сформировать второй массив всех таких различных чисел, которые ни разу в первом массиве не встречаются и имеют величину больше минимального и меньше максимального из чисел первого массива.

Сформировать массив:
Y[1]=A[1]+A[n]
Y[2]= A[2]+A[n-1]
Y[3]= A[3]+A[n-2]
и т.д. (n — четное)

Даны два одномерных массива А и В. Подсчитайте количество тех i, для которых:
а) А[i] B[i]

Даны два целочисленных массива одинаковой размерности. Получить третий массив той же размерности, каждый элемент которого равен большему из соответствующих элементов данного массива.

Определить величину максимальной разности между соответствующими элементами двух массивов и записать на то же место в третий массив той же размерности.

Даны два одномерных массива одинаковой длины. Получить третий массив такой же размерности, каждый элемент которого равен сумме соответствующих элементов данных массивов, умноженной на больший из них.

Источник

Перестановка элементов массива

Перестановка двух элементов

Пример 1

Поменять местами два элемента массива А с задан­ными координатами (номерами строки и столбца).

Решение

Можно эту задачу решить несколькими способами. Первый способ аналогичен перестановке элементов в одномерном массиве, когда в процедуру передаются индексы элементов и массив, в котором надо их поме­нять. Тогда процедура может быть такой:

Program Example_124;

Procedure Swap1(k1, l1, k2, l2: Integer;

Var c: Integer;

Begin

c:=x[k1, l1]; x[k1, l1]:=x[k2,l2];

End;

Второй способ. Вспомним процедуру Swap, кото­рая меняет местами значения двух целых переменных.

Program Example_125;

Procedure Swap(Varx, у: Integer);

Var z: Integer;

Begin

End;

А теперь обратимся к ней, передавая данные эле­менты: Swap(A[k1, l1], A[k2, l2]).

Рассмотрим задачу о перестановке двух столбцов (строк), так как многие задачи используют это действие.

Пример 2

Поменять местами столбцы с номерами l1 и l2. Эту задачу также можно решить несколькими спо­собами. Составим процедуру, в которую будем переда­вать номера столбцов, и массив, в котором надо их переставить. Кроме того, добавим проверку коррект­ности ввода данных номеров, так как если столбца с данным номером нет, то и переставлять ничего не надо. В самой процедуре можно использовать, например, процедуру Swap

Program Example_126;

Procedure Swap2(l1, l2: Integer;

Var i: Integer;

Begin

If (l1 m)) Or (l2 m)) Then

Writeln (‘Ввод неправильный’)

Swap(x[i, l1], x[i, l2]);

End;

Если применять первую процедуру Swap1, то после проверки правильности ввода данных будет такое обра­щение:

Swap1(i, l1, i, l2, x);

СТРОКОВЫЙ ТИП ДАННЫХ

Описание

Строкой называется последовательность заданной дли­ны, состоящая из символов.

Строки (переменные типа String) могут быть объяв­лены, например, следующим образом:

Var Str1: String[30]; Str2: String;

При объявлении строковой переменной в квадрат­ных скобках может указываться длина строки. Если дли­на строки не указана, то она принимается равной 255. Максимальная длина строки также равна 255. В дан­ном случае в первой строке может содержаться макси­мум 30 символов, а во второй − 255. Надо заметить, что строка похожа на одномерный массив символов: она имеет определенную длину (не больше некоторого числа), к каждому символу можно обратиться по его номеру (как в массиве) – Str1[i] − это обраще­ние к i−му элементу строки Str1.

Переменные типа String выводятся на экран по­средством стандартных процедур Write и Writeln и вводятся с помощью стандартных процедур Readln и Read. To есть вводятся и выводятся не поэлементно, как массивы, а целиком.

Примечание. Если при вводе задать символов больше, чем максимально допустимо, то лишние символы будут проигно­рированы.

Операции со строками

В Паскале имеется два основных способа обработки переменных типа String. Первый способ предпола­гает обработку всей строки как единого целого, т.е. единого объекта. Кроме того (это второй способ), мож­но рассматривать строку как составной объект, состоя­щий из отдельных символов, то есть элементов типа Char, которые при обработке доступны каждый в от­дельности.

Склеивание

Под склеиванием понимается последовательное объе­динение нескольких строк.

Пример

Var Str1, Str2, Str3: String[20];

Строка Str3 имеет значение ‘У Егорки всегда отго’. В данном примере максимальная длина стро­ки Str3 равна 20 символам, поэтому будут взяты только первые 20 символов суммы строк, а остальные рассматриваться не будут. Паскаль позволяет выпол­нять операции объединения (сцепления) нескольких строк в процессе их присвоения какой-либо перемен­ной: Str3:= ‘У Егорки ‘+’ всегда ‘+’ отговорки’. В результате такой операции в пере­менной Str3 будет то же самое содержимое, что и в предыдущем примере.

Примечание. «Склеить» строки можно также при помо­щи функции

Concat(Str1, Str2. StrN).

Сравнение

Паскаль позволяет выполнять операции сравнения двух строк. Сравнение происходит посимвольно слева направо: сравниваются коды соответствующих симво­лов до тех пор, пока не нарушится равенство или не кончится одна из строк (или обе сразу), при этом сра­зу делается вывод о знаке неравенства. Две строки на­зываются равными, если они равны по длине и совпа­дают посимвольно.

Пример

‘balkon’>’balk’ (длина первой строки больше);

‘кошка ‘>’кошка’ (длина первой строки больше);

‘кот’=’кот’ (равны по длине и совпадают посимвольно).

Можно использовать любые операции отношения (>, , >=, =

Источник

Уроки 34 — 36
§ 20. Обработка массивов

Содержание урока

Перестановка элементов массива

Перестановка элементов массива

Во многих задачах нужно переставлять элементы массива, т. е. требуется менять местами значения двух ячеек памяти.

Представьте себе, что в кофейной чашке налит сок, а в стакане — кофе, и вы хотите, чтобы было наоборот. Что вы сделаете?

Вернёмся к программированию. Чтобы поменять местами значения двух переменных — а и b, нужно использовать третью переменную того же типа:

Перестановка двух элементов массива, например А [i] и А [к], выполняется так же:

Теперь рассмотрим несколько задач, в которых требуется переставить элементы массива в другом порядке.

Задача 1. Массив А содержит чётное количество элементов N. Нужно поменять местами пары соседних элементов: первый со вторым, третий — с четвёртым и т.д. (рис. 4.1).

С каким элементом нужно поменять местами элемент А [i]? Зависит ли ваш ответ от свойств числа i?

Сергей написал такой алгоритм для решения задачи 1:

нц для i от 1 до N

поменять местами A[i] и A[i+1]

кц

Выполните его вручную для массива <1, 2, 3, 4>(N = 4). Объясните результат. Найдите ошибки в этом алгоритме.

Обратите внимание, что на последнем шаге цикла мы будем менять местами элемент А [ N ] с несуществующим элементом A [N+1 ]. Это вызовет ошибку, которая называется выход за границы массива. Но даже если изменить наибольшее значение переменной цикла на N-1, программа всё равно будет работать неправильно, т. е. приведёт к неверному решению задачи 1. Получится, что первый элемент просто «переедет» на место последнего.

Для того чтобы исправить программу, нужно изменять переменную i с шагом 2:

Решение на языке Паскаль получилось немного более сложным, потому что в этом языке можно изменять переменную цикла только с шагом 1 или -1, а нам нужен шаг 2. В этой ситуации можно, например, использовать цикл с условием (цикл while).

Предложите другое решение этой задачи, записав нужные операторы в теле цикла.

Следующая страница Реверс массива

Cкачать материалы урока

Источник

Зона кода

Задача, разумеется, оказалась сложной именно для меня. Но, при этом, и очень интересной. Вот её условие, обнаруженное на просторах Интернета:

Условие задачи приведено в том виде, в котором было обнаружено. Важнейшую роль в условии играет замечание, содержащее два дополнительных условия. Для незнакомых с O-символикой объясню их смысл.

Первое условие заключается в том, что дополнительная память, выделяемая для решения задачи, должна быть постоянной, т. е. не должна зависеть от n. Если бы этого условия не было, то задача решалась бы очень просто. Достаточно было бы создать массив того же размера, что и исходный, скопировать в него все элементы, после чего переписать их обратно, расположив их в требуемом порядке. Задача, имеющая такое простое решение, не была бы достойной нашего рассмотрения.

Второе условие содержит понятие «сложность». Под сложностью можно понимать количество элементарных операций, которое требуется совершить, чтобы решить задачу для конкретного n. К таким операциям можно отнести, например, перемещение элемента с одной позиции на другую или транспозицию элементов. Те операции, количество которых фиксировано и не зависит от n, при подсчёте сложности можно не учитывать.

Обозначим символом c_n сложность алгоритма, позволяющего решить задачу для для заданного n. Второе условие заключается в том, что, говоря бытовым языком, c_n при увеличении n должно расти «медленнее», чем n 2 . Ну, а на математическом языке это требование можно записать так:

lim n → ∞ c n n 2 = 0 .

Поскольку размер дополнительной памяти не может зависеть от размера массива, то придётся ограничиться или циклическими перестановками элементов, или транспозициями, которые, впрочем, являются частным случаем циклических перестановок.

Циклические перестановки — тупиковый путь?

Первая же идея, которая пришла мне в голову — воспользоваться циклическими перестановками. Выбираем какой-либо элемент массива (за исключением первого и последнего, т. к. они уже расположены на «своих» местах), выталкиваем его из «старого» места и перемещаем на своё место, предварительно вытолкнув из него находящийся там другой элемент. Этот элемент помещаем на его «законное» место, вытолкнув до этого оттуда некоторый третий элемент. Далее продолжаем эти действия до тех пор, пока элемент, вытолкнутый последним, не займёт то место, на котором находился первый элемент.

В результате все элементы, участвующие в данной циклической перестановке, окажутся на своих местах. Но проблема заключается в том, что могут остаться элементы, в ней не участвовавшие и находящиеся на чужих местах.

Таким образом, мы можем придти к следующей ситуации: часть элементов уже находится на своих местах, а часть — на чужих. И не будет у нас тогда никакой возможности различать элементы, относящиеся к этим двум группам, ведь перемещения мы нигде не фиксируем, поскольку дополнительная память по условию постоянна.

Возможно, существует способ перебора всех элементов, принадлежащих разным циклическим цепочкам. В этом случае можно было бы для каждого такого элемента инициировать циклическую перестановку, в результате чего все элементы оказались бы на своих местах. Но идей, которые позволили бы «соорудить» такой способ, у меня не нашлось.

В итоге, я решил отказаться от идеи циклических перестановок, что, впрочем, не означает, что решения, на них основанного, не существует.

Рекурсивный алгоритм. Частный случай

Следующая идея, посетившая меня, — свести задачу для массива к двумя задачам для полумассивов. Это можно сделать с помощью последовательно выполняемых транспозиций — операций, меняющих местами два элемента массива.

Наиболее легко придуманный мною алгоритм описать для случая, когда число элементов массива (обозначим его буквой m) представляет собой натуральную степень двойки, т. е. m = 2 k , где k — натуральное.

Если k = 1, то никаких действий не предпринимаем. В противном случае разбиваем массив на 4 равные части и меняем местами вторую и третью четверти. Для этого нужно выполнить транспозицию каждого элемента второй четверти с соответствующим ему элементом третьей четверти. Таким образом, число всех транспозиций будет в 4 раза меньше числа элементов в массиве.

В результате описанной операции каждый из элементов массива оказывается расположенным в «своей» половине массива. Таким образом, каждую из половин можно теперь обрабатывать независимо от другой. Именно такая обработка и является следующим шагом. Каждую из половин массива снова подвергаем операциям, описанным для исходного массива. Это продолжается до тех пор, пока не дойдёт дело до обработки 4-элементных «подмассивов», после которой элементы исходного массива оказываются расположенными в нужном нам порядке.

Кстати, тот же принцип (сведение исходной задачи для массива к идентичным задачам для двух его частей) лежит и в основе алгоритма быстрой сортировки.

Давайте рассмотрим действие описанного алгоритма на примере массива, состоящего из m = 16 элементов (при этом n = 8). Схематично весь процесс изображён на рисунке ниже.

Схема обработки 16-элементного массива

Элементы массива изображены в виде кружков, причём белый цвет соответствует элементам, обозначенным в условии буквой a с индексом, а чёрный — обозначенным буквой b с индексом. Под каждым кружком имеется число, «жёстко» с ним связанное (т. е. кружки будут перемещаться вместе с соответствующими им числами). Это число представляет собой место элемента, которое он должен занимать в окончательно преобразованном массиве. Таким образом, в результате работы алгоритма цвета кружков должны чередоваться, а связанные с ними числа должны располагаться в порядке возрастания от 1 до 16.

На схеме имеются 4 изображения массива, соединённых стрелками. Стрелки означают шаги, посредством которых изменяются порядки расположения элементов в массиве. Как мы видим, наша задача решается в три шага.

На первом шаге элементы массива, стоящие на местах 5, 6, 7, 8 меняются местами с элементами 9, 10, 11, 12 соответственно. На первом изображении массива все 8 элементов, подлежащих перемещению, обведены прямоугольной пунктирной рамкой. На втором изображении они расположены на новых местах, а сам массив разделён короткой вертикальной чертой на две равные части, которые, в дальнейшем, будут преобразовываться независимо друг от друга.

На втором шаге элементы, стоящие на местах 3, 4 меняются местами с элементами, стоящими на местах 5, 6 соответственно, а стоящие на местах 11, 12 — соответственно со стоящими на местах 13, 14 (все эти 8 элементов выделены двумя прямоугольными рамками на втором изображении). На третьем изображении эти элементы уже стоят на новых местах, а сам массив разбит вертикальными чертами на 4 равных части.

На третьем шаге транспозиции подвергаются 2-й и 3-й элементы, 6-й и 7-й, 10-й и 11-й, 15-й и 14-й. Эти элементы выделены на третьем изображении уже четырьмя прямоугольными рамками. Как можно заметить, третий шаг приводит нас к искомому результату (см. четвёртое изображение массива).

Итак, на каждом из 3-х шагов было выполнено по 4 транспозиции. Таким образом, общее число транспозиций для m = 16 равно 12. В общем случае для обработки массива из m = 2 k элементов потребуется k — 1 шагов, причём, на каждом шаге будет осуществлено по 2 k — 2 транспозиций.

Давайте за сложность c_n алгоритма, обрабатывающего массив из m = 2n элементов примем количество необходимых для такой обработки транспозиций. Получаем:

c n = k — 1 2 k — 2 .

k = log 2 2 n = log 2 2 + log 2 n = 1 + log 2 n .

c n = 1 + log 2 n — 1 2 1 + log 2 n — 2 = log 2 n · 2 log 2 n — 1 = 1 2 n log 2 n = n ln n 2 ln 2 .

lim n → ∞ c n n 2 = lim n → ∞ n ln n 2 ln 2 n 2 = 1 2 ln 2 lim n → ∞ ln n n = 1 2 ln 2 · 0 = 0 .

Здесь мы использовали хорошо известный из математического анализа факт, состоящий в том, что n является бесконечно большой более высокого порядка, чем ln n. Итак, как мы видим, сложность алгоритма удовлетворяет требованию задачи. Кстати, саму сложно можно оценить следующим образом: c_n = O(n ln n).

А будет ли при реализации алгоритма выполнено требование к дополнительной памяти? Об этом мы поговорим ближе к концу статьи.

Реализация алгоритма для частного случая

Создадим функцию transform() , реализующую алгоритм, описанный в предыдущем разделе. Она будет принимать в качестве аргументов адрес обрабатываемого массива и число n (половину размера массива). Код функции приведён ниже.

Как мы видим, код достаточно простой. Если массив содержит только 2 элемента, то обработка не требуется, поэтому функция заканчивает работу (см. строки 3, 4). В противном случае в цикле for выполняются необходимые транспозиции элементов. Предварительно в переменной p сохраняется индекс первого обрабатываемого элемента (строка 5), который совпадает с числом выполняемых транспозиций.

Если в цикле выполнена лишь одна транспозиция, то на этом обработка массива заканчивается. В противном случае массив разбивается на 2 половины, и функция transform() рекурсивно вызывается для каждой из них (см. строки 12-16). Обратите внимание на то, что во втором рекурсивном вызове (строка 15) функции передаётся адрес не массива, а элемента, являющегося первым во второй половине массива. Функция transform() , очевидно, будет работать корректно, вне зависимости от того, обрабатывает ли она массив целиком или лишь его часть.

Протестируем функцию transform() . Половину размера обрабатываемого массива зададим с помощью макроса N , который определим следующим образом:

Тестирование будет осуществляться функцией main() , из которой будет вызываться функция print_arr() , выводящая массив на печать. Вот код этих функций:

В функции main() создаётся целочисленный массив , состоящий из 2 * N элементов. Первая его половина заполняется нечётными числами от 1 до 2 * N — 1 , а вторая — чётными от 2 до 2 * N . Таким образом, после обработки массива, он, в случае успеха, должен быть заполнен числами от 1 до 2 * N .

Далее массив выводится на печать с помощью функции print_arr() . Затем для обработки массива вызывается функция transform() , после чего уже преобразованный массив снова печатается посредством print_arr() .

В результате работы программы на консоль выводится следующий текст:

Как видим, массив, состоящий из 16 элементов, был обработан корректно.

Рекурсивный алгоритм для исходной задачи

Возвращаемся к исходной задаче. Напоминаю, что мы построили алгоритм, корректно обрабатывающий массивы, чьи размеры являются степенями двойки. Нам нужно изменить его таким образом, чтобы он обрабатывал массивы произвольных чётных размеров.

В процессе модификации уже готового алгоритма нам нужно решить две проблемы.

1. Исходный массив всегда имеет чётный размер. Но если он не совпадает со степенью числа 2, то при очередном рекурсивном вызове функция transform() обязательно столкнётся с необходимостью обрабатывать массив, состоящий из нечётного числа элементов, чего она делать «не умеет».
2. Даже если размер массива чётен, половина размера может быть нечётной. В этом случае процесс разбиения массива на четыре равные части с последующей транспозицией второй и третьей четвертей невозможен.

Решение первой проблемы заключается в дополнении массива, состоящего из нечётного числа элементов, одним «фиктивным» элементом. В итоге, функция transform() всегда будет получать для обработки массив из чётного числа элементов.

Опишем принцип, по которому происходит дополнение. Понятно, что нечётные массивы образуются парами после разбиения массива, имеющего чётное, но не делящееся на 4 число элементов, на две равные части. Так вот, массив, содержащий элементы из первой половины исходного массива, нужно дополнить фиктивным элементом справа, а массив, содержащий элементы из второй половины, нужно дополнить фиктивным элементом слева.

Далее массивы, имеющие, благодаря фиктивным элементам, чётное число элементов, подвергаются дальнейшей обработке. Заметим, что, поскольку она никогда не затрагивает крайних элементов, то фиктивные элементы в ходе обработки перемещаться не буду.

Вторая проблема решается достаточно просто. Нужно использовать следующую разбивку массива. Первая часть должна иметь тот же размер, что и четвёртая, а вторая — тот же, что и третья, но при этом размер первых двух должен быть на единицу больше размера двух последних. Как и в исходной версии алгоритма, транспозиции должны подвергаться вторая и третья части массива.

Продемонстрируем работу новой версии алгоритма на примере обработки массива, состоящего из 10 элементов. Схема обработки приведена ниже.

Схема обработки 10-элементного массива

Как мы видим, вторая проблема возникает ещё перед первым шагом. Решение её продемонстрировано посредством прямоугольной пунктирной рамки, охватывающей 4 элемента, которые на первом шаге будут перемещены. Разбиение на 4 части проводится таким образом, что первая и четвёртая включают в себя по 3 элемента, а вторая и третья — по 2.

После выполнения первого шага возникает уже первая проблема: полумассивы содержат по 5 элементов. Она решается введением двух фиктивных элементов, обозначенных на схеме кружками с крестиками внутри.

В ходе выполнения второго шага снова уже понятным образом решается вторая проблема. После реализации второго шага мы приходим к необходимости обработки 4-х подмассивов по 3 элемента в каждом. Снова прибегаем к дополнению этих массивов 4-мя фиктивными элементами.

После того, как третий шаг выполнен, мы получаем массив, в котором интересующие нас (т. е. не фиктивные) элементы расположены в требуемом порядке. Остаётся удалить фиктивные элементы, и мы получаем окончательный результат.

Реализация алгоритма для общего случая

Изменим функцию transform() таким образом, чтобы она работала с массивами любых чётных размеров. Главный вопрос, который может волновать читателя — «Каким образом вводить в массив фиктивные элементы?». Ответ на него очень прост: никаких фиктивных элементов в массив мы добавлять не будем. Роль фиктивных элементов в подмассивах будут играть соседние по отношению к соответствующим крайним элементам этих подмассивов элементы, принадлежащие исходному массиву. Фактически, мы будем просто «расширять» подмассивы в ту или иную сторону. Ни к каким неприятным последствиям такой подход не приведёт, поскольку фиктивные элементы, как мы помним, в ходе выполнения алгоритма никуда не перемещаются.

Ниже приведён код новой версии функции transform() .

Обратите внимание на переменную odd , которая объявляется и инициализируется в строке 5. Она играет ключевую роль в данной версии функции transform() . Значение odd устанавливается равным единице, если полуразмер текущего обрабатываемого массива (т. е. число n, хранящееся в формальном параметре n ) нечётен и нулю в противном случае.

Если n нечётно, то в цикле for начальное значение переменной цикла i устанавливается на единицу большим, чем целая часть от n / 2. Таким образом решается вторая проблема, описанная в предыдущем размере.

Для решения первой проблемы (опять же, при нечётном n) мы, во-первых, на единицу увеличиваем размер массивов, который будет передаваться в функцию transform() при двух рекурсивных вызовах (см. строку 12). Во-вторых, мы смещаем левую границу второго массива на один элемент влево (см. строку 16 и ср. с 15-й строкой предыдущей версии). Правая граница первого массива и так будет смещена на один элемент вправо благодаря увеличению размера массива на единицу.

Заметим, что в случае чётности n все действия, выполняемые данной версией функции transform() , будут абсолютно эквивалентны действиям, выполняемым первой версией.

Для тестирования новой версии transform() будем использовать те же функции main() и print_arr() , которые использовались в предыдущем разделе. Однако макрос N мы переопределим следующим образом:

Выполнение тестовой программы приводит к следующему выводу на консоль:

С обработкой массива из 10 элементов наша программа справилась успешно. Читатель, при желании, сам сможет протестировать работу программы при других значениях размера массива.

А решена ли задача?

Итак, алгоритм, выполняющий необходимые перестановки элементов массива, построен и реализован. Но, чтобы ответить на вопрос, вынесенный в заголовок раздела, нам нужно понять, выполнены ли требования, касающиеся сложности алгоритма и размера дополнительной памяти.

Что касается сложности, то было показано, что для количества элементов массива, являющегося степенью двойки, она представляет собой O(n lnn). Можно показать, что то же утверждение будет справедливо и для произвольного чётного количества элементов. Таким образом, требование к сложности алгоритма выполнено.

А выполняется ли требование к дополнительной памяти? С одной стороны, мы, в ходе обработки исходного массива, не прибегаем к выделению дополнительной памяти, размер которой зависел бы от n. Но мы прекрасно понимаем, что за нас это автоматически делает компьютер для того, чтобы обеспечить цепочку рекурсивных вызовов функции transform() .

Действительно, при любом вызове функции (разумеется, мы не говорим сейчас о встраиваемых функциях) автоматически выделяется стековая память для хранения локальных переменных, используемых в этой функции. Давайте оценим объём памяти, задействованной при рекурсивных вызовах функции transform() .

Обратимся к самому первому примеру — обработке 16-элементного массива. Максимальное количество одновременно запущенных на выполнение экземпляров функции transform() (назовём его глубиной рекурсии) совпадает с количеством шагов алгоритма; в данном случае оно равна 3.

В более общем случае, при обработке массива из 2 k элементов глубина рекурсии составляет k — 1. Как мы установили ранее, k = 1 + log₂ n, поэтому глубина рекурсии через n выражается так: log₂ n. А поскольку объём дополнительной памяти пропорционален глубине рекурсии, то можно сделать вывод о том, что он представляет собой O(ln n). Можно показать, что такая же оценка объёма дополнительной памяти справедлива и для общего случая, когда размер массива является произвольным чётным числом.

Итак, наше решение имеет сложность O(n ln n) и задействует дополнительную память объёмом O(ln n). Получить решение, имеющее ту же сложность, но использующее дополнительную память, объём которой не зависит от n, не удалось. Возможно, существует решение, принципиально отличающееся от предложенного мною, удовлетворяющее всем требованиям задачи. А можно ли переделать рекурсивную функцию в нерекурсивную, т. е. реализующую наш алгоритм посредством итераций, причём такую, которая не задействует память, объём которой зависит от n? На этот вопрос у меня ответа нет.

Фактом является то, что любую рекурсивную реализацию любого алгоритма можно переделать в итеративную, но не факт, что при этом можно обойтись без затрат памяти, объём которой зависит от количества итераций. Например, я встречал итерационные реализации упоминавшегося ранее алгоритма быстрой сортировки, по своей природе являющегося рекурсивным, однако в них использовался стек, размер которого как раз зависел от числа итераций.

Добавлю, что первый вариант функции transform() (работающий только для случаев m = 2 k ) я смог бы переделать в приемлемый (т. е. не потребляющий память, зависящую от n) итерационный. Но как переделать второй, «универсальный» вариант, я пока не знаю.

Если в дальнейшем мне удастся улучшить полученное решение, то статья будет обновлена. А кто знает, может улучшенное решение предложит читатель? Если это случится, то я буду очень рад!

Источник