Способы передачи вращательного движения.
Передача – устройство, главная функция которого передача энергии на расстояние, в зависимости от способа передачи энергии, они могут быть: механические, электрические, пневматические, гидравлические. Механической передачей называется механизм, который преобразует параметры движения источника энергии (двигателя) при передаче исполнительным органам, в этом случае передача осуществляет согласование параметров движения двигателя и исполнительного рабочего органа.
Передачи вращательного движения по способу соединения тел вращения бывают: 1) передачи с контактом тел вращения – зубчатые, червячные, фрикционные, винтовые, 2) передачи гибкой связью – ремённые и цепные; по способу передачи движения – передачи с зацеплением (зубчатые, червячные, цепные), трением – ременные и фрикционные. Электри́ческая переда́ча — обеспечивает передачу тягового усилия от первичного двигателя к движителю или исполнительному органу, используя электрически соединённые электрогенератор и электродвигатель.
Сложное движение. Плоскопараллельное движение тела.
Плоскопаралле́льное движе́ние — вид движения абсолютно твёрдого тела, при котором траектории всех точек тела располагаются в плоскостях, параллельных заданной плоскости.
Примером плоскопараллельного движения по отношению к вертикальной плоскости, относительно которой тело движется в параллельном направлении, является качение колеса по горизонтальной дороге.
Пример плоскопараллельного движения относительно плоскости чертежа — качение колеса по горизонтальной дороге. Все точки колеса движутся параллельно плоскости рисунка.
Здесь плоскопараллельное движение в каждый момент времени может быть представлено в виде суммы двух движений — полюса C, являющегося не чем иным, как центром вращения колеса в связанной с ним системе координат (в общем случае по любой траектории на плоскости с точки зрения неподвижного наблюдателя) и вращательного движения остальных точек тела вокруг этого центра.
Вращение тела в случае его плоско-параллельного движения не является необходимым признаком последнего. В таком случае вектор абсолютной скорости движения любой точки будет определяться векторной суммой переносной скорости движения центра вращения С, (одинаковой для расчёта скорости любой точки колеса). И вектора относительной скорости выбранной точки, зависящей от её положения, угловой скорости вращения и расстояния от центра.
Если в данный момент для точки контакта колеса с поверхностью (точки А) эти скорости равны по модулю и противоположны по направлению, имеет место случай чистого (без проскальзывания) качения, что показано на рисунке. Только в этом случае скорость точки М будет в 2 раза больше скорости точки С и направлена в ту же сторону. В общем случае их соотношение может быть любым не только по величине, но и по направлению.
Сложное движения. Определение скорости любой точки тела.
Теорема 1. Абсолютная скорость 
любой точки плоской фигуры в каждый данный момент равна геометрической сумме двух скоростей: скорости 
произвольно выбранного полюса в поступательном движении плоской фигуры и вращательной скорости 
во вращательном движении фигуры относительно полюса.
Положение любой точки В тела можно определить равенством:
Взяв производную от обеих частей уравнения по времени получим,
где 
— искомая скорость; 
— скорость полюса; 
— скорость точки В при вращательном движении тела вокруг полюса А при 
Таким образом
, 
Теорема 2. Проекции скоростей двух точек плоской фигуры на ось, проходящую через эти точки, равны и имеют одинаковый знак. Зная, что 
, спроецируем данное выражение на прямую АВ, тогда
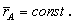
Теорема 3. Плоская фигура в каждый момент времени имеет одну точку, абсолютная скорость которой равна нулю. Эта точка называется мгновенным центром скоростей (МЦС), обозначим ее буквой Р. Докажем существование МЦС 
тогда точка Р и будет искомой.
,
Источник
Передачи вращательного движения
Передача – устройство, главная функция которого передача энергии на расстояние, в зависимости от способа передачи энергии, они могут быть: механические, электрические, пневматические, гидравлические. В курсе деталей машин мы будем изучать только механические передачи вращательного движения.
Механической передачей называется механизм, который преобразует параметры движения источника энергии (двигателя) при передаче исполнительным органам, в этом случае передача осуществляет согласование параметров движения двигателя и исполнительного рабочего органа.
Передачи вращательного движения по способу соединения тел вращения бывают: 1) передачи с контактом тел вращения – зубчатые, червячные, фрикционные, винтовые, 2) передачи гибкой связью – ремённые и цепные; по способу передачи движения – передачи с зацеплением (зубчатые, червячные, цепные), трением – ременные и фрикционные.
3.10.1. Кинематические и силовые параметры передач
Это параметры, характеризующие вращательное движение элементов передач:
1) Частота вращения, n (об/мин), выражается через угловую скорость (рад/с):
, (3.14)
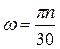
2) Крутящий момент на валу T, Нм
3) Окружная скорость (Н) – сила вызывающая вращение тел или сопротивление вращению и направленная по касательной к траектории точки ее приложения.
, (3.15)
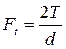
4) Мощность на валу, Р, Вт:
; (3.16)
. (3.17)
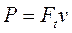
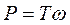
3.10.2. Передаточное отношение и КПД механизма
Отношение угловых скоростей ведущих и ведомых тел называется передаточным отношением.
. (3.18)
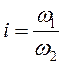
Для одноступенчатого редуктора:
, (3.19)
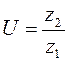
Передаточное отношение привода состоящего из нескольких передач, расположенных последовательно, равно произведению передаточных чисел всех его передач.
, (3.20)
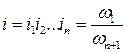
где n – число передач, входящих в привод.
КПД привода равен отношению мощности на ведомом и ведущем валах:
, (3.21)
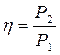
В общем случае КПД привода состоящего из нескольких передач равен произведению КПД передач входящих в привод:
. (3.22)
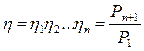
3.10.3. Ременные и цепные передачи
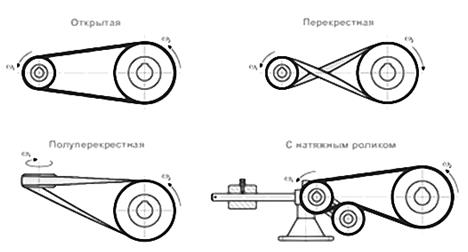
Передача вращения посредством ремня, надетого на шкивы, называется ременной передачей (Рис. 3.18).
Рис. 3.18. Ременные передачи
Ременные передачи применяют преимущественно в тех случаях, когда по условиям конструкции валы расположены на значительных расстояниях или высокие скорости не позволяют применять другие виды передач.
Ременные передачи бывают: По форме поперечного сечения ремня: плоскоременные (а), клиноременные (б), круглоременные (г) а также передачи с зубчатыми ремнями (в, д, е) (Рис. 3.19).
Рис. 3.19. Формы поперечного сечения ремней
Плоскоременные передачи более простые по конструкции, однако, клиноременные обладают большей нагрузочной способностью.
Ременные передачи по расположению осей валов подразделяются:
1) Открытыми с параллельно расположенными осями валов и вращением шкивов в одном направлении, 2) перекрестные, с параллельными осями валов и вращением шкивов в противоположных направлениях, 3) полуперекрестные со скрещивающими осями валов, 4) угловые со скрещивающимися или пересекающимися осями валов.
По способу натяжения ремня: с периодическим натяжением (перемещением опоры шкива); с автоматическим натяжением (натяжным роликам).
Преимущества ременных передач: 1) возможность больших межосевых расстояний, 2) плавность работы, гашение ударов за счет эластичности ремня и возможности проскальзывания, 3) простота конструкции и эксплуатации, 4) возможность передачи большого диапазона мощностей и скоростей, 5) относительно высокий КПД.
Недостатки: 1) относительно большие размеры передачи, 2) непостоянство передаточного отношения вследствие проскальзывания, 3) повышенная нагрузка на валы от натяжения ремня, 5) не долговечность ремней в среднем 2-3 тысячи часов работы.
Материал ремней: материал ремня должен обеспечивать надежность сцепления со шкивами и достаточную долговечность. Самые распространенные – резинотканевые ремни, кожаные, хлопчатобумажные цельнотканые, полимерные.
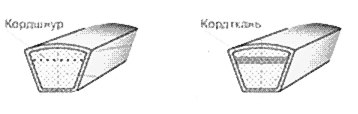
Клиновые ремни наиболее распространены и имеют трапециидальное сечение и выпускается 2-х типов: корд-шнуровые (а) и корд-тканевые (б) (Рис. 3.20). Корд шнуровые ремни более гибкие и долговечные поэтому применяются для более сложных условий работы.
Рис. 3.20. Типы клиновых ремней
3.10.4. Расчет и проектирование ременных передач
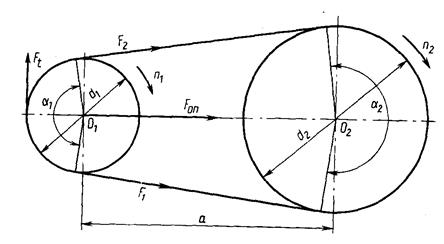
Основными критериями работоспособности ременных передач являются: тяговая способность, определяемая силой трения между ремнем и шкивом; долговечность ремня, которая в условиях нормальной эксплуатации ограничивается разрушением от усталости (Рис. 3.21).
Геометрические параметры ременных передач: аw – межосевое расстояние передачи, d 1 и d2 – диаметры ведущего и ведомого шкивов, α1, α2 – угол обхвата ведущего и ведомого шкивов.
1) Передаточное отношение передачи:
. (3.23)
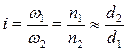
Рис. 2.21. Схема ременной передачи
С учетом скольжения ремня:
. (3.24)
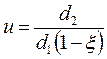
где ξ(дзетта) – коэффициент скольжения ремня ξ = 0,01…0,02.
Передаточное отношение ременной передачи обычно не превышает шести;
2) Скорость ремня
. (3.25)
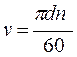
3) Угол обхвата меньшего шкива
. (3.26)
. (3.27)
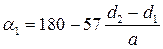
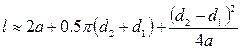
3.10.5. Силовые взаимодействия в ременной передаче
Окружная сила ременной передачи:
, (3.28)
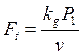
где F1 – натяжение ведущей ветви,
F2 – натяжение ведомой ветви.
Р1 – мощность на ведомом шкиву,
V – скорость ремня,
кg – коэффициент динамической нагрузки.
Окружная скорость равна:
, (3.29)
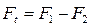
Сила начального натяжения:
, (3.30)
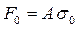
где А – площадь поперечного сечения ремня,
σ0 — начальное напряжение в ремне.
, (3.31)
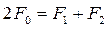
Решая совместно выражения (3.30) и (3.31) получим:
; (3.32)
. (3.33)
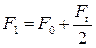
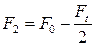
Уравнения (3.32, 3.33) представляют систему 2-х уравнений с тремя неизвестными, для его решения Эйлером было получено уравнение, представляющее собой зависимость между силой трения ремня о шкив и тяговой способностью передачи:
, (3.34)
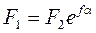
где е = 2,71, f – коэффициент трения ремня о шкив, α 
— угол обхвата шкива ремнем.
Решая совместно уравнения (3.30) и (3.34) получим выражения:
, (3.35)
, (3.36)
. (3.37)
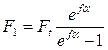
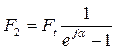
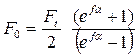
Формулы (3.36 и 3.37) устанавливают связь сил натяжения ветвей работающей передачи с величиной нагрузки Ft и факторами трения (f и α). Они позволяют также определить минимально необходимую величину предварительного натяжения ремня F0 , при которой еще возможна передача заданной нагрузки Ft:
Если: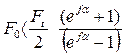 
, (3.38)
то в передаче начнется буксование ремня.
Тяговая способность передачи характеризуется величиной максимально допустимой окружной силы Ft или полезного напряжения σF,учитывая формулы (3.34-3.36), можно сделать вывод, что допустимое по условию отсутствия буксования напряжение возрастает с увеличением напряжения от предварительного натяжения σ0:
. (3.39)
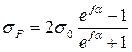
Практика показывает, что происходит значительное снижение долговечности ремня с увеличением σ0.
Силы натяжения ветвей ремня передаются на валы и опоры. Равнодействующая нагрузку можно определить по формуле:
. (3.40)
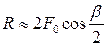
Обычно R в два, три раза больше окружной силы Ft.
Источник
