Способы передачи открытого ключа

Шифрование с открытым ключом: Наглядная иллюстрация

Просто и наглядно о сложном: Асимметричная криптография с открытым ключом.

Долгое время традиционная криптография использовала шифрование с тайным или симметричным ключом — один и тот же ключ использовался как для зашифровывания, так и для расшифровки (дешифрования) данных.

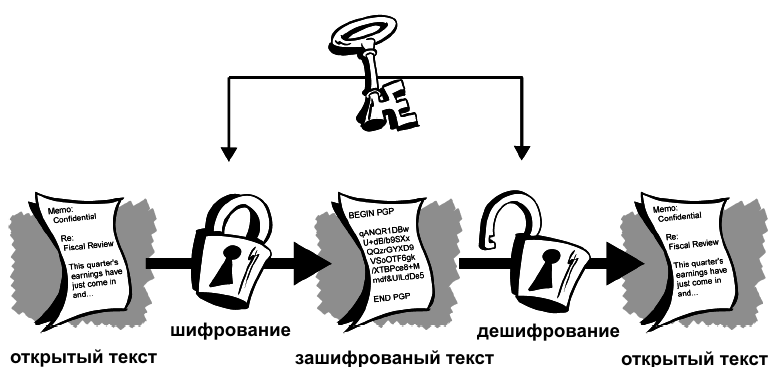
Наглядно это можно представить в виде замка, которым запирался сундук с тайным сообщением. Пара одинаковых ключей к этому замку была как у отправителя сообщения ( шифровальщика), так и у получателя ( дешифровальщика).

Разумеется, в действительности никто не отправлял сообщения в запертых сундуках. Тексты, которые надо было зашифровать, особым образом видоизменялись с использованием тайного ключа (шифра) — последовательности символов, которая смешиваясь с передаваемым сообщением особым образом (называемым алгоритмом шифрования), приводила к получению шифровки ( шифротекста) — сообщения, которое невозможно было прочитать, не зная алгоритма и шифра (ключа).

Но для наглядности процесса, мы представим, что наше сообщение помещалось в некий прочный сундук и закрывалось надежным навесным замком, одинаковые ключи от которого были у обеих сторон — отправителя и получателя.

Вот этот ключ, которым запиралось (зашифровывалось) и открывалось (дешифровывалось) сообщение, назывался шифром или тайным симметричным ключом.

Проблема была в том, что при смене ключа (шифра) в целях безопасности, его необходимо было доставить получателю, который зачастую находился далеко и на враждебной территории. Передавать шифр открытыми каналами связи было небезопасно.

Долгое время проблема безопасной передачи нового ключа (шифра) оставалась неразрешенной. Как правило, для этого использовали тайных курьеров, что не гарантировало на 100% того, что шифр (ключ) не попадет к нежелательным лицам, которые смогут им воспользоваться для дешифрования тайных сообщений.

Проблема с ключами была решена только в 1975 году, когда Уитфилд Диффи (Bailey Whitfield ‘Whit’ Diffie) и Мартин Хеллман (Martin E. Hellman) предложили концепцию шифрования с парой ключей: открытым (публичным — public key), который зашифровывает данные, и соответствующим ему закрытым (приватным — private key).

Эта асимметричная система шифрования получила название криптографии с открытым ключом.

Работает эта система так:

• Генерируется случайный закрытый (приватный) ключ (напомним, что ключ или шифр — это последовательность символов) и по определенному алгоритму подбирается к нему другой — открытый (публичный) ключ. При этом, для любого закрытого ключа существует только один вариант открытого. Т.е. эти ключи (приватный и публичный) всегда работают в паре (связке).
• Далее полученный открытый (публичный) ключ пересылается по любым открытым каналам связи отправителю тайного сообщения.
• Получив открытый (публичный) ключ, отправитель при помощи него зашифровывает сообщение и отправляет его получателю у которого есть соответствующий закрытый (приватный) ключ.
• Получатель расшифровывает секретное сообщение, используя свой закрытый (приватный) ключ из пары с открытым (публичным), которым было зашифровано сообщение.

Следует отметить, что открытым (публичным) ключом можно только зашифровать сообщение, но расшифровать его уже этим ключом не получится. Для дешифрования нужен только закрытый (приватный) ключ из пары. Так работает алгоритм с асимметричным шифрованием.

Но, вернемся к нашему сундуку с сообщением. Как же теперь наглядно представить асимметричное шифрование? Как так можно — запирать одним ключом, а отпирать другим?

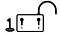
Представим себе навесной замок с двумя замочными скважинами и двумя ключами (см.рис. ниже) — левый ключ (1) через левую замочную скважину (1) может снимать фиксацию с левой половинки дуги замка, освобождая ее и открывая весь замок. Правый ключ (2) через правую замочную скважину (2) может фиксировать правую половинку дуги в замке, тем самым закрывая замок. Но, после закрытия, этот ключ (2) не может уже освободить от фиксации правую часть дуги и тем самым открыть замок.

Первоначально замок с зафиксированной левой половинкой дуги (1) и расфиксированной правой (2), а также с ключом 2 (открытым) доставляется лицу, которое должно отправить тайное послание.

Получив замок и открытый ключ (2), отправитель навешивает его на сундук с тайным посланием и запирает его полученным ключом 2. Теперь сундук закрыт и даже отправитель не может его открыть, поскольку его ключ (2) может только зафиксировать правую часть дуги в замке, но не может освободить от фиксации.

Запертый замком сундук с тайным посланием отправляется получателю, у которого есть ключ (1), снимающий фиксацию правой половинки дуги и тем самым отпирающий замок. Но, другие лица, даже если они будут иметь копию публичного ключа (2), открыть замок не смогут.

Получатель открывает замок ключом (1) и тайное послание прочитано!

Пользуясь терминологией асимметричной криптографии с открытым ключом, ключ 1 — это закрытый (приватный) ключ, а ключ 2 — это открытый (публичный) ключ.

В заключение отметим, что асимметричная криптография с открытым ключом получила широкое распространение, и не только в шифровании шпионских и дипломатических посланий. Асимметричную криптографию используют сайты с поддержкой протокола HTTPS, мессенджеры, wifi-роутеры, банковские системы и многое другое. На основе асимметричной криптографии базируется электронная подпись. Также на асимметричной криптографии построен алгоритм блокчейна, на котором, в свою очередь построены все криптовалюты, включая биткоин.

© Иллюстрации к тексту:

• Первые две — из книги «Введение в криптографию», Филипп Циммерман.
• Остальные — автора (Сергей Базанов)
• Титульная картинка — Husch Blackwell

Источник

Криптография с открытым ключом

Основные требования к алгоритмам асимметричного шифрования

Создание алгоритмов асимметричного шифрования является величайшим и, возможно, единственным революционным достижением в истории криптографии.

Алгоритмы шифрования с открытым ключом разрабатывались для того, чтобы решить две наиболее трудные задачи, возникшие при использовании симметричного шифрования .

Первой задачей является распределение ключа . При симметричном шифровании требуется, чтобы обе стороны уже имели общий ключ , который каким-то образом должен быть им заранее передан. Диффи, один из основоположников шифрования с открытым ключом , заметил, что это требование отрицает всю суть криптографии, а именно возможность поддерживать всеобщую секретность при коммуникациях.

Второй задачей является необходимость создания таких механизмов, при использовании которых невозможно было бы подменить кого-либо из участников, т.е. нужна цифровая подпись . При использовании коммуникаций для решения широкого круга задач, например в коммерческих и частных целях, электронные сообщения и документы должны иметь эквивалент подписи, содержащейся в бумажных документах. Необходимо создать метод, при использовании которого все участники будут убеждены, что электронное сообщение было послано конкретным участником. Это более сильное требование, чем аутентификация .

Диффи и Хеллман достигли значительных результатов, предложив способ решения обеих задач, который радикально отличается от всех предыдущих подходов к шифрованию.

Сначала рассмотрим общие черты алгоритмов шифрования с открытым ключом и требования к этим алгоритмам. Определим требования, которым должен соответствовать алгоритм , использующий один ключ для шифрования, другой ключ — для дешифрования , и при этом вычислительно невозможно определить дешифрующий ключ , зная только алгоритм шифрования и шифрующий ключ .

Кроме того, некоторые алгоритмы, например RSA , имеют следующую характеристику: каждый из двух ключей может использоваться как для шифрования, так и для дешифрования .

Сначала рассмотрим алгоритмы, обладающие обеими характеристиками, а затем перейдем к алгоритмам открытого ключа , которые не обладают вторым свойством.

При описании симметричного шифрования и шифрования с открытым ключом будем использовать следующую терминологию. Ключ , используемый в симметричном шифровании , будем называть секретным ключом . Два ключа, используемые при шифровании с открытым ключом , будем называть открытым ключом и закрытым ключом . Закрытый ключ держится в секрете, но называть его будем закрытым ключом , а не секретным, чтобы избежать путаницы с ключом, используемым в симметричном шифровании . Закрытый ключ будем обозначать KR , открытый ключ — KU .

Будем предполагать, что все участники имеют доступ к открытым ключам друг друга, а закрытые ключи создаются локально каждым участником и, следовательно, распределяться не должны.

В любое время участник может изменить свой закрытый ключ и опубликовать составляющий пару открытый ключ , заменив им старый открытый ключ .

Диффи и Хеллман описывают требования, которым должен удовлетворять алгоритм шифрования с открытым ключом .

1. Вычислительно легко создавать пару ( открытый ключ KU, закрытый ключ KR ).
2. Вычислительно легко, имея открытый ключ и незашифрованное сообщение М , создать соответствующее зашифрованное сообщение:

Можно добавить шестое требование, хотя оно не выполняется для всех алгоритмов с открытым ключом :

Это достаточно сильные требования, которые вводят понятие односторонней функции с люком . Односторонней функцией называется такая функция, у которой каждый аргумент имеет единственное обратное значение, при этом вычислить саму функцию легко, а вычислить обратную функцию трудно.

Y = f(X) — легко

X = f -1 (Y) — трудно

Обычно «легко» означает, что проблема может быть решена за полиномиальное время от длины входа. Таким образом, если длина входа имеет n битов, то время вычисления функции пропорционально n a , где а — фиксированная константа. Таким образом, говорят, что алгоритм принадлежит классу полиномиальных алгоритмов Р. Термин «трудно» означает более сложное понятие. В общем случае будем считать, что проблему решить невозможно, если усилия для ее решения больше полиномиального времени от величины входа. Например, если длина входа n битов, и время вычисления функции пропорционально 2 n , то это считается вычислительно невозможной задачей. К сожалению, тяжело определить, проявляет ли конкретный алгоритм такую сложность. Более того, традиционные представления о вычислительной сложности фокусируются на худшем случае или на среднем случае сложности алгоритма. Это неприемлемо для криптографии, где требуется невозможность инвертировать функцию для всех или почти всех значений входов.

Вернемся к определению односторонней функции с люком , которую, подобно односторонней функции , легко вычислить в одном направлении и трудно вычислить в обратном направлении до тех пор, пока недоступна некоторая дополнительная информация. При наличии этой дополнительной информации инверсию можно вычислить за полиномиальное время. Таким образом, односторонняя функция с люком принадлежит семейству односторонних функций f_k таких, что

Y = fk(X) — легко, если k и Х известны

X = fk -1 (Y) — легко, если k и Y известны

Х = fk -1 (Y) — трудно, если Y известно, но k неизвестно

Мы видим, что разработка конкретного алгоритма с открытым ключом зависит от открытия соответствующей односторонней функции с люком .

Криптоанализ алгоритмов с открытым ключом

Как и в случае симметричного шифрования , алгоритм шифрования с открытым ключом уязвим для лобовой атаки. Контрмера стандартная: использовать большие ключи.

Криптосистема с открытым ключом применяет определенные неинвертируемые математические функции . Сложность вычислений таких функций не является линейной от количества битов ключа, а возрастает быстрее, чем ключ. Таким образом, размер ключа должен быть достаточно большим, чтобы сделать лобовую атаку непрактичной, и достаточно маленьким для возможности практического шифрования. На практике размер ключа делают таким, чтобы лобовая атака была непрактичной, но в результате скорость шифрования оказывается достаточно медленной для использования алгоритма в общих целях. Поэтому шифрование с открытым ключом в настоящее время в основном ограничивается приложениями управления ключом и подписи, в которых требуется шифрование небольшого блока данных.

Другая форма атаки состоит в том, чтобы найти способ вычисления закрытого ключа , зная открытый ключ . Невозможно математически доказать, что данная форма атаки исключена для конкретного алгоритма открытого ключа . Таким образом, любой алгоритм, включая широко используемый алгоритм RSA , является подозрительным.

Наконец, существует форма атаки, специфичная для способов использования систем с открытым ключом . Это атака вероятного сообщения. Предположим, например, что посылаемое сообщение состоит исключительно из 56-битного ключа сессии для алгоритма симметричного шифрования. Противник может зашифровать все возможные ключи , используя открытый ключ , и может дешифровать любое сообщение, соответствующее передаваемому зашифрованному тексту. Таким образом, независимо от размера ключа схемы открытого ключа , атака сводится к лобовой атаке на 56-битный симметричный ключ . Защита от подобной атаки состоит в добавлении определенного количества случайных битов в простые сообщения.

Основные способы использования алгоритмов с открытым ключом

Основными способами использования алгоритмов с открытым ключом являются шифрование/ дешифрование , создание и проверка подписи и обмен ключа.

Шифрование с открытым ключом состоит из следующих шагов:

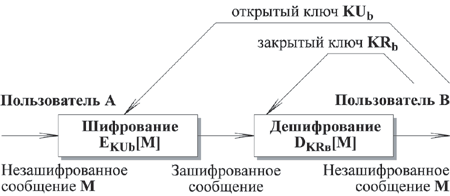
1. Пользователь В создает пару ключей KU_b и KR_b , используемых для шифрования и дешифрования передаваемых сообщений.
2. Пользователь В делает доступным некоторым надежным способом свой ключ шифрования, т.е. открытый ключ KU_b . Составляющий пару закрытый ключ KR_b держится в секрете.
3. Если А хочет послать сообщение В , он шифрует сообщение, используя открытый ключ В KU_b.
4. Когда В получает сообщение, он дешифрует его, используя свой закрытый ключ KR_b . Никто другой не сможет дешифровать сообщение, так как этот закрытый ключ знает только В .

Если пользователь (конечная система) надежно хранит свой закрытый ключ , никто не сможет подсмотреть передаваемые сообщения.

Создание и проверка подписи состоит из следующих шагов:

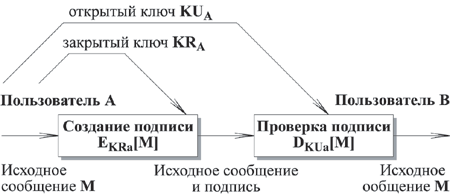
1. Пользователь А создает пару ключей KR_A и KU_A , используемых для создания и проверки подписи передаваемых сообщений.
2. Пользователь А делает доступным некоторым надежным способом свой ключ проверки, т.е. открытый ключ KU_A . Составляющий пару закрытый ключ KR_A держится в секрете.
3. Если А хочет послать подписанное сообщение В , он создает подпись E_KRa[M] для этого сообщения, используя свой закрытый ключ KR_A .
4. Когда В получает подписанное сообщение, он проверяет подпись D_KUa[M] , используя открытый ключ А KU_A . Никто другой не может подписать сообщение, так как этот закрытый ключ знает только А .

До тех пор, пока пользователь или прикладная система надежно хранит свой закрытый ключ , их подписи достоверны.

Кроме того, невозможно изменить сообщение, не имея доступа к закрытому ключу А ; тем самым обеспечивается аутентификация и целостность данных .

В этой схеме все сообщение подписывается, причем для подтверждения целостности сообщения требуется много памяти. Каждое сообщение должно храниться в незашифрованном виде для использования в практических целях. Кроме того, копия сообщения также должна храниться в зашифрованном виде, чтобы можно было проверить в случае необходимости подпись. Более эффективным способом является шифрование небольшого блока битов, который является функцией от сообщения. Такой блок, называемый аутентификатором , должен обладать свойством невозможности изменения сообщения без изменения аутентификатора . Если аутентификатор зашифрован закрытым ключом отправителя, он является цифровой подписью , с помощью которой можно проверить исходное сообщение. Далее эта технология будет рассматриваться в деталях.

Важно подчеркнуть, что описанный процесс создания подписи не обеспечивает конфиденциальность. Это означает, что сообщение, посланное таким способом, невозможно изменить, но можно подсмотреть. Это очевидно в том случае, если подпись основана на аутентификаторе, так как само сообщение передается в явном виде. Но даже если осуществляется шифрование всего сообщения, конфиденциальность не обеспечивается, так как любой может расшифровать сообщение, используя открытый ключ отправителя.

Обмен ключей: две стороны взаимодействуют для обмена ключом сессии , который в дальнейшем можно использовать в алгоритме симметричного шифрования.

Некоторые алгоритмы можно задействовать тремя способами, в то время как другие могут использоваться одним или двумя способами.

Перечислим наиболее популярные алгоритмы с открытым ключом и возможные способы их применения.

Источник