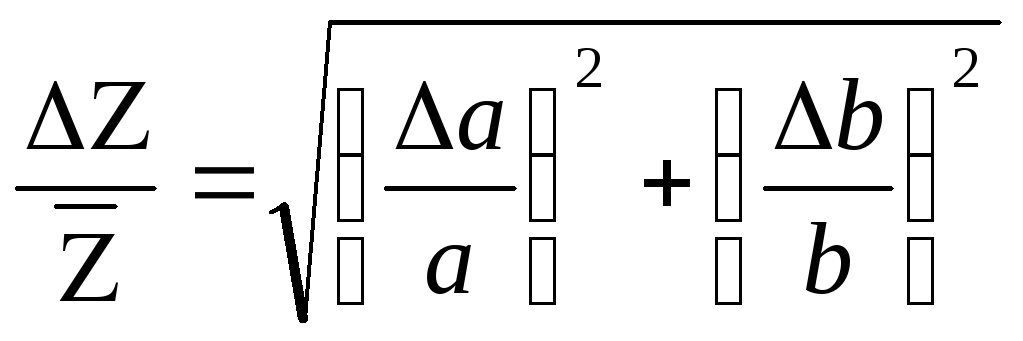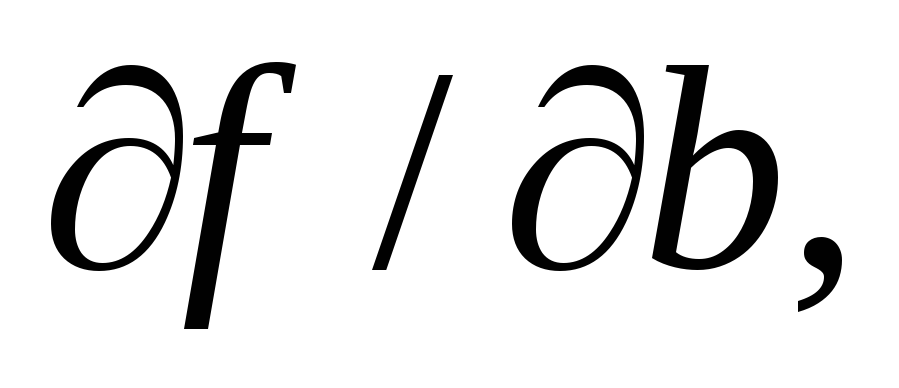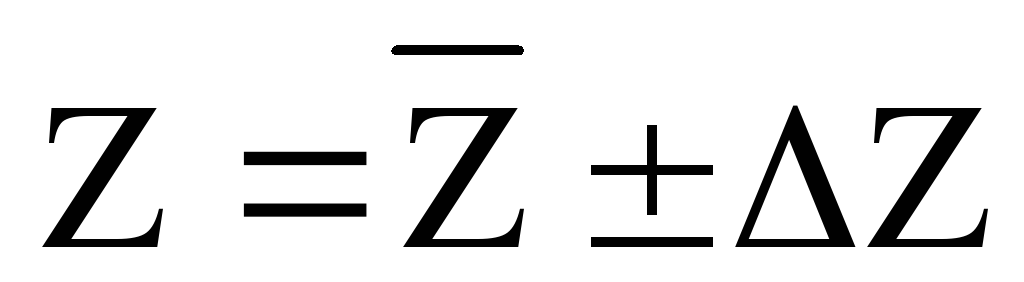Способы оценки погрешности при косвенных измерениях
Погрешности прямых измерений. Промах. Систематическая погрешность. Случайная погрешность. Полная погрешность. Погрешности косвенных измерений. Запись результата измерений
- Оценка погрешности прямых измерений
Измерить физическую величину – это значит сравнить ее с однородной величиной, принятой за единицу меры.
Различают прямые и косвенные измерения.
Если измеряемая величина непосредственно сравнивается с мерой, то измерения называются прямыми. Например, измерения линейных размеров тел с помощью масштабной линейки и т.д.
Если измеряется не сама искомая величина, а некоторые другие величины, связанные с ней функциональной зависимостью, то измерения называются косвенными. Например, измерения объема, ускорения и т.д.
Из-за несовершенства средств и методик измерения, органов чувств при любом измерении неизбежны отклонения результатов измерений от истинных величин. Эти отклонения называются погрешностями измерений.
Погрешности измерений делятся на систематические, случайные и промахи.
1.1. Промахи, связанные с неправильными отсчетами по прибору, неправильными записями и т.д., приводят к очень большой по абсолютной величине погрешности. Они, как правило, не укладываются в общую закономерность измеренных величин. Обнаруженный промах следует отбросить.
1.2. Систематическими погрешностями Δxсист называются погрешности, которые сохраняются при повторных измерениях одной и той же величины x или изменяются по определенному закону.
Систематические погрешности подразделяются на несколько групп. Отметим только приборную погрешность.
Систематическая приборная погрешность определяется по классу точности прибора, который указывается на приборе следующими цифрами: 0,01; 0,02; 0,05; 1,0; 2,5; 4,0. Класс точности показывает предельно допустимое значение систематической погрешности, выраженной в процентах от верхнего предела на выбранном диапазоне измерений. Например, предел измерения вольтметра с классом точности 0,5 равен 200 В. Систематическая погрешность равна 0,5% от 200В. Следовательно, систематическая погрешность вольтметра равна 1 В.
Если на приборе класс точности не указан, то погрешность равна половине цены наименьшего деления шкалы прибора.
1.3. Случайными называются погрешности, которые изменяются беспорядочно при повторных измерениях одной и той же физической величины при одинаковых условиях.
Оценим случайную погрешность. Пусть при измерении какой-либо физической величины было произведено N измерений и были получены значения x1, x2, … xN. Тогда наиболее вероятным значением измеряемой величины является ее среднее арифметическое значение
Результаты измерений x1, x2, … xN «рассеиваются» вокруг среднего. В качестве меры «рассеяния» результатов наблюдения вокруг среднего служит среднее квадратичное отклонение
Пусть a будет истинным, но неизвестным значением измеряемой величины x. Доказано, что вероятность попадания результатов измерения величины x в интервал значений от (a – S) до (a + S) оказывается равной α = 0,68.
Вероятность попадания результатов наблюдений в более широкие интервалы (a – 2S, a + 2S) и (a – 3S, a + 3S) равна α = 0,95 и α = 0,99 соответственно.
Вероятность попадания в заданный интервал значений величины x называется доверительной вероятностью, а сам интервал – доверительным интервалом.
Однако, таким образом полученный доверительный интервал справедлив при большом значении N. В учебных лабораториях, как правило, приходится ограничиваться небольшим числом измерений. В этом случае доверительный интервал находят с помощью коэффициента Стьюдента, который зависит от числа измерений N и доверительной вероятности α. В таблице 1 приведены коэффициенты Стьюдента для различного числа наблюдений при доверительных вероятностях α = 0,68; 0,95; 0,99.
Источник
Способы оценки погрешности при косвенных измерениях
Чтобы найти погрешность косвенных измерений, надо воспользоваться формулами, приведенными в таблице. Эти формулы могут быть выведены «методом границ».
Сначала надо вспомнить основные понятия теории погрешности.
Абсолютная погрешность физической величины ΔА — это разница между точным значением физической величины и ее приближенным значением и измеряется в тех же единицах, что и сама величина:
Так как мы никогда не знаем точного значения величины А, а лишь определяем из опыта ее приближенное значение, то и величину абсолютной погрешности мы можем определить лишь приблизительно. Наиболее просто находится максимальная величина абсолютной погрешности, которая и используется нами в лабораторных работах.
Относительная погрешность измерения εА равна:
При косвенных измерениях величину погрешности искомой величины вычисляют по формулам:
В случае, когда искомая величина находится по формуле, в которой в основном присутствуют произведение и частное, удобней находить сначала относительную погрешность. Если при этом один из множителей представляет собой сумму или разность, нужно предварительно найти его абсолютную погрешность (сложением абсолютных погрешностей слагаемых), а затем относительную.
Зная относительную погрешность, найти абсолютную погрешность измерений можно так:
«Правило ничтожных погрешностей»
при суммировании погрешностей любым из слагаемых можно пренебречь, если оно не превосходит ⅓ – ⅟ 4 от другого.
Запись результата с указанием погрешности.
Абсолютная погрешность измерений обычно округляется до 1 значащей цифры, а, если эта цифра 1, то до двух.
Результат записывается в виде:
А = Аизм ± ΔА, например: ℓ = (13 ± 2) мм.
При этом в измеренном значении следует оставлять столько десятичных знаков, сколько их в значении погрешности (последняя цифра погрешности «поправляет» последнюю цифру измеренного значения) . Значение величины и погрешность следует выражать в одних и тех же единицах!
Пример оценки погрешностей косвенных измерений № 1
Пример оценки погрешностей косвенных измерений № 2
Задания для самостоятельного решения
Задание 1. Найдите плотность вещества, из которого сделан куб со стороной 7,00 ± 0,15 см, если его масса 847 ± 2 г. Что это за вещество?
Задание 2. Найдите удельную теплоту сгорания топлива, 2,10 ± 0,15 г которого хватило, чтобы нагреть 400 ± 10 мл воды на 35°С ± 2°С. Что это за топливо?
© Ивашкина Д.А., 2017. Публикация материалов с сайта разрешена только при наличии активной ссылки на главную страницу.
Источник
6.Оценка погрешности при косвенных измерениях.
Чаще всего интересующая нас величина не получается непосредственно из измерений, а вычисляется как функция измеренных значений каких–то других величин. Рассмотрим случай, когда искомая величина Z является функцией нескольких переменных a, b, с,…, значения которых определяются непосредственно из серий измерений:
Z=
Будем считать (это справедливо в подавляющем большинстве случаев), что погрешности измерений 

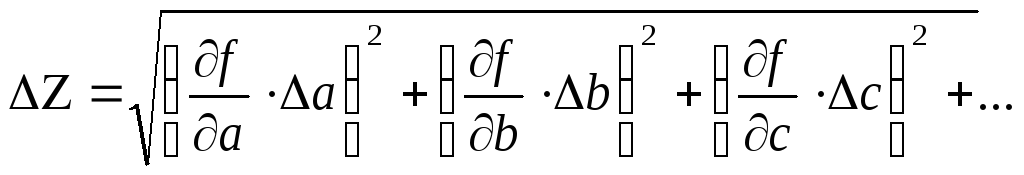
Здесь 
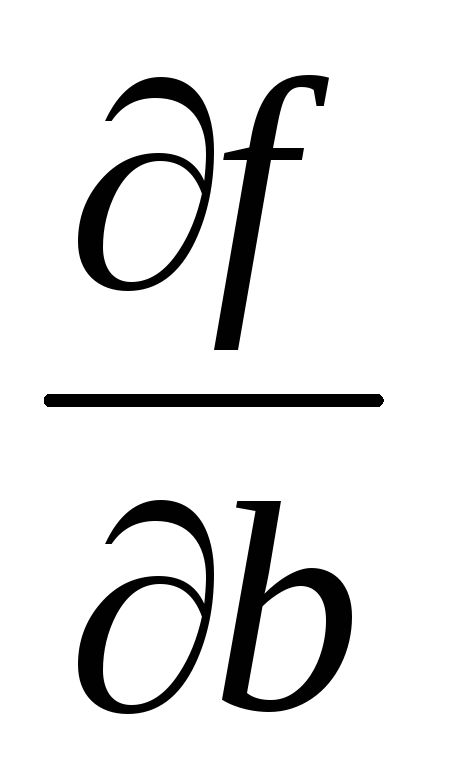
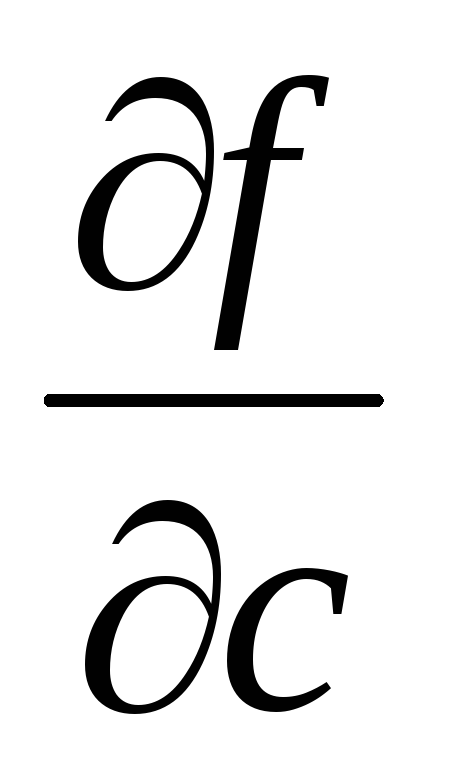


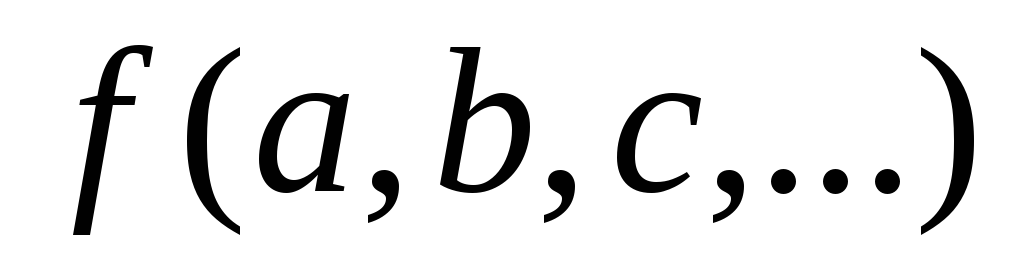



Относительная погрешность величины Z=f(a, b, c,…)
будет определяться по формуле:
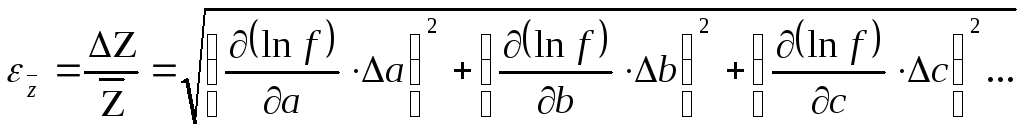
Для того, чтобы можно было найти явный вид формулы для расчета погрешности косвенных измерений, не зная правил нахождения производственной функции, в Приложении 2 приведены формулы для нахождения абсолютной и относительной погрешности наиболее типичных функций. В частности, если Z=a+b, то


Если 

Приведем общую схему оценки погрешности косвенных измерений.
Для каждой серии измерений величины а, b, c, входящих
в определение искомой величины 
2. Вычисляется среднее значение результата косвенных измерений:

3. По формулам (6.1) и (6.2) или с помощью таблицы Приложения 2 находятся выражения для абсолютной или относительной погрешности искомой величины, исходя из конкретного вида функциональной зависимости 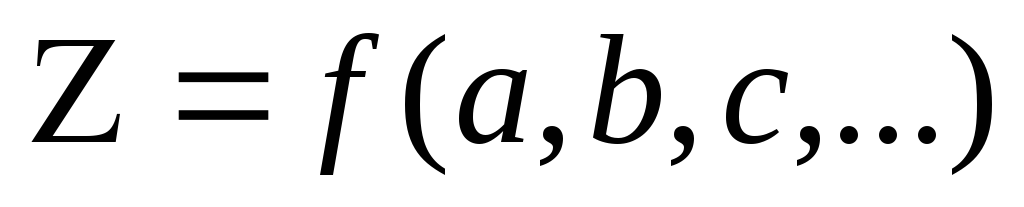

Какую из величин 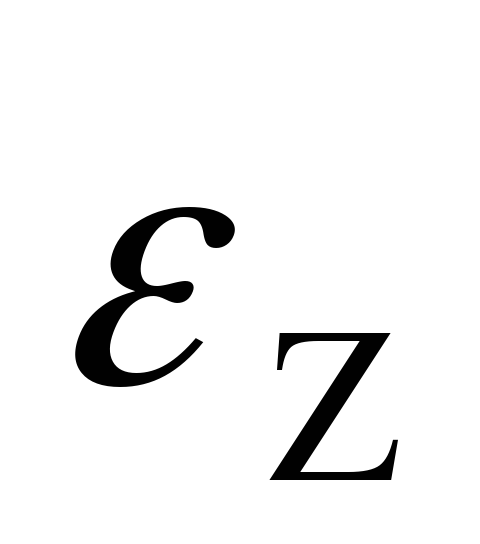


4.По полученной в п.3 формуле для абсолютной (или относительной) погрешности вычисляется значение 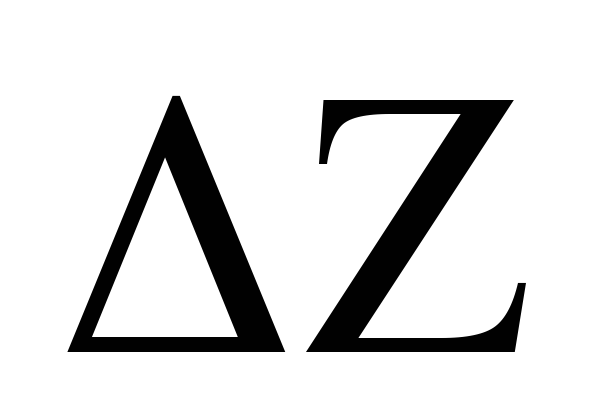



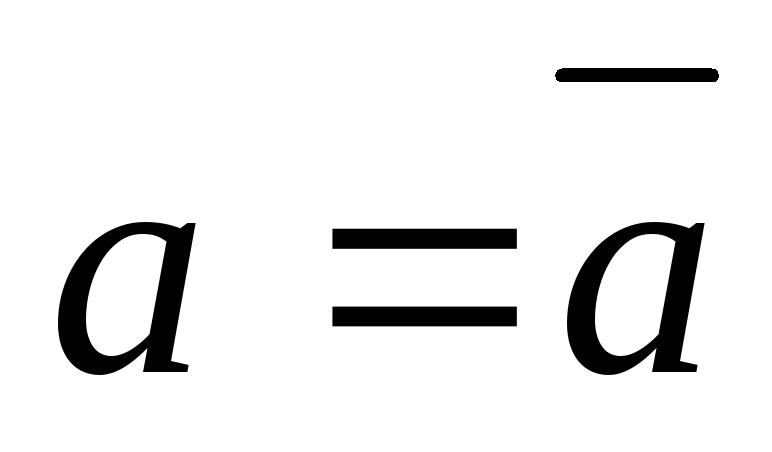

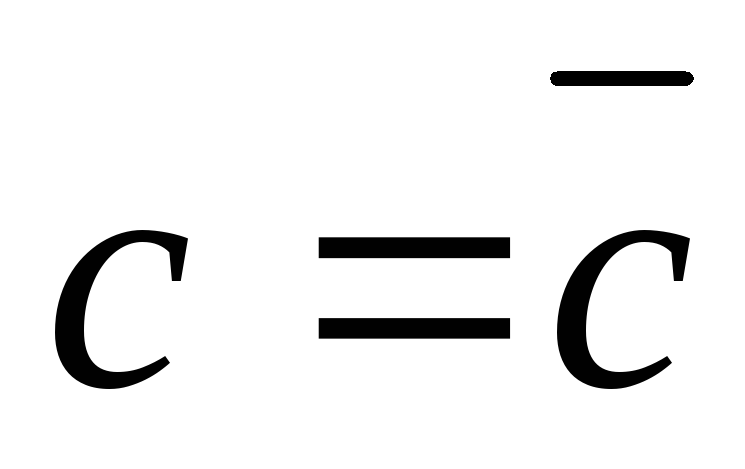
5. Окончательный результат записывают в виде:
Замечание 1. В ряде случаев обработку результатов косвенных измерений проводят отличным от изложенного выше способом. Значения функции 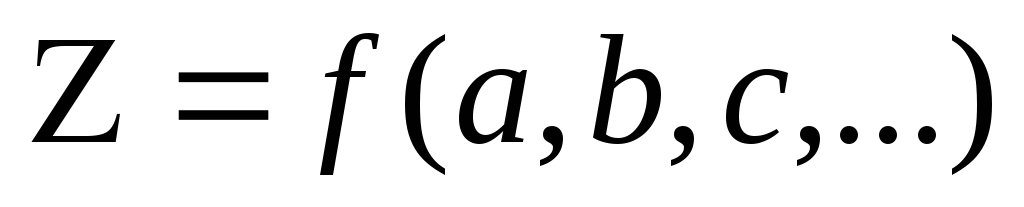


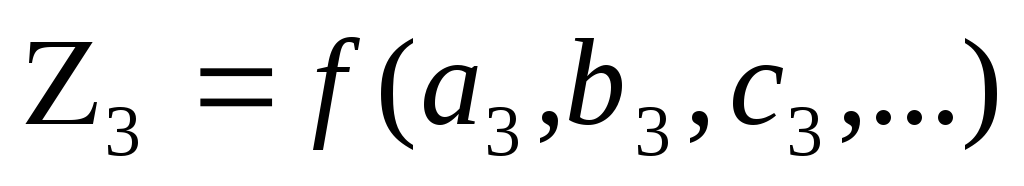


Замечание 2. При нахождении результата косвенных измерений иногда необходимо использовать значения величин, известные из других, ранее проведенных измерений. Например, при нахождении ускорения свободного падения с помощью математического маятника (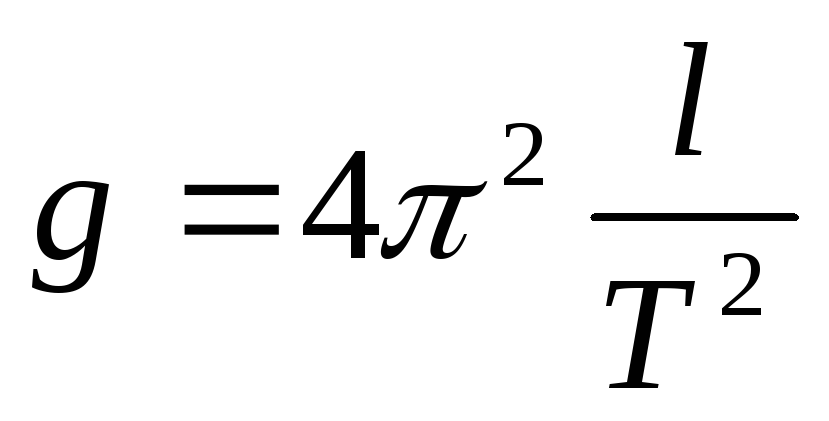






Рассмотрим конкретные примеры.
Пример 2. Вычислить погрешность измерения площади сечения проволоки. Диаметр проволоки измеряется микрометром, количество измерений равно пяти. Пусть результаты измерения диаметра в точности такие же как и в пример 1. т.е. 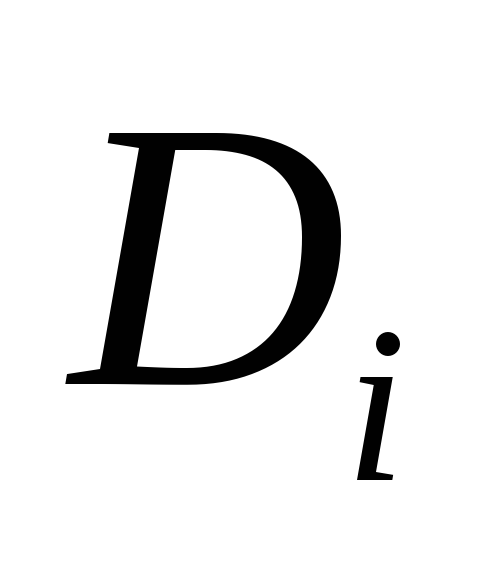
Расчет погрешности прямых измерений здесь проводить не будем (он детально рассмотрен в примере 1). Приведем окончательный результат: 



Вычислим среднее значение площади сечения 
Найдем выражение для расчета относительной погрешности:
Вычислим относительную погрешность:
Вычисляем абсолютную погрешность:

Запишем окончательный результат:


Пример 3. Вычислить погрешность определения ускорения свободного падения g с помощью математического маятника. Величина g определяется выражением:

где l—длина математического маятника:
T –период колебаний;
t–время, за которое совершается N колебаний.
Пусть длина l измеряется три раза сантиметровой линейкой:
1.Обработка прямых измерений (li и ti) производится в соответствии со схемой параграфа 5. Приведем окончательные результаты:
l= (1,85 

t=(54,6



2.Вычислим среднее значение 

3.Определим для расчета относительной погрешности
4.Вычислим относительную погрешность:
Вычислим абсолютную погрешность:

5.Запишем окончательный результат:


Источник