 Open Source Content Management
Open Source Content Management
Nav view search
Навигация
Искать
Main Menu
Измерение ошибок и выбор метода прогнозирования
В ходе процесса прогнозирования неизбежно возникают ошибки прогноза. Под ошибкой прогноза понимают расхождение между прогнозом и действительностью. Хотя в прогнозировании считается, что, до тех пор, пока значение прогноза находится в доверительных границах, эти расхождения не являются ошибкой.
Ошибки прогноза могут возникать по разным причинам и иметь различные источники. Их можно разделить на систематические, возникающие из-за погрешности измерения, и случайные. К источникам систематических ошибок относятся недостаточное количество прямых переменных, использование некорректной зависимости между переменными, применение неверной трендовой линии, ошибочный сдвиг сезонного спроса и наличие необнаруженного тренда во временных рядах. К случайным ошибкам относятся те ошибки, которые нельзя объяснить используемой моделью прогноза.
Измерение ошибок прогноза производится с помощью таких показателей, как среднее абсолютное отклонение, среднеквадратическое отклонение, средняя абсолютная относительная ошибка и средняя относительная ошибка.
Среднее абсолютное отклонение (МАD) представляет собой среднее значение ошибки в прогнозе, которое измеряет разброс прогнозируемых значений от ожидаемых. МАD вычисляют как разность между действительным и прогнозируемым спросом без учета знака, по следующей формуле:

где t – номер периода;
А – текущий спрос данного периода;
F – прогнозируемый спрос данного периода;
n – общее количество периодов.
Определение среднеквадратического отклонения (MSE) также основано на вычислении отклонений от средней арифметической, однако при ее вычислении используют не абсолютные величины, а квадраты величин отклонений. Она определяется по формуле:

Показатель MSE позволяет выявить отдельные большие отклонения от фактических данных. На основе MSE можно отобрать такие способы прогнозирования, которые стабильно дают приемлемые средние ошибки, и отсеять такие способы, которые характеризуются, как правило, малыми ошибками, но допускающие иногда очень большую погрешность.
Средняя абсолютная относительная ошибка (МАРЕ) применяется в том случае, если для определения показателя общей ошибки удобнее использовать не абсолютные, а относительные величины.

В случае, когда требуется оценить, насколько смещенными (т.е. завышенными или заниженными) являются результаты прогнозирования, то можно использовать показатель средней относительной ошибки МРЕ.

Если показатель МРЕ близок к нулю, то смещения нет. Если он отрицательный, то имеет место завышение прогнозных оценок; если положительный, то оценки будут заниженными.
При сравнении двух и более методов прогнозирования, чем меньше рассмотренные выше показатели, тем более точный прогноз.
Выбор метода прогнозирования зависит от временных и затратных факторов. При нехватке времени и средств целесообразно использовать простые и дешевые методы прогнозирования, такие как модели на основе скользящих средних или экспоненциальное сглаживание. Для проверки надежности какого-либо метода прогнозирования можно использовать разные методы измерения ошибок прогноза.
Источник
Методы оценки качества прогноза
Часто при составлении любого прогноза — забывают про способы оценки его результатов. Потому как часто бывает, прогноз есть, а сравнение его с фактом отсутствует. Еще больше ошибок случается, когда существуют две (или больше) модели и не всегда очевидно — какая из них лучше, точнее. Как правило одной цифрой (R 2 ) сложно обойтись. Как если бы вам сказали — этот парень ходит в синей футболке. И вам сразу все стало про него ясно )
В статьях о методах прогнозирования при оценке полученной модели я постоянно использовал такие аббревиатуры или обозначения.
- R 2
- MSE
- MAPE
- MAD
- Bias
Попробую объяснить, что я имел в виду.
Остатки
Суровые MSE и R 2
Когда нам требуется подогнать кривую под наши данные, то точность этой подгонки будет оцениваться программой по среднеквадратической ошибке (mean squared error, MSE). Рассчитывается по незамысловатой формуле 
где n-количество наблюдений.
Соотвественно, программа, рассчитывая кривую подгонки, стремится минимизировать этот коэффициент. Квадраты остатков в числителе взяты именно по той причине, чтобы плюсы и минусы не взаимоуничтожились. Физического смысла MSE не имеет, но чем ближе к нулю, тем модель лучше.
Вторая абстрактная величина это R 2 — коэффициент детерминации. Характеризует степень сходства исходных данных и предсказанных. В отличии от MSE не зависит от единиц измерения данных, поэтому поддается сравнению. Рассчитывается коэффициент по следующей формуле: 
где Var(Y) — дисперсия исходных данных.
Безусловно коэффициент детерминации — важный критерий выбора модели. И если модель плохо коррелирует с исходными данными, она вряд ли будет иметь высокую предсказательную силу. 
MAPE и MAD для сравнения моделей
Статистические методы оценки моделей вроде MSE и R 2 , к сожалению, трудно интерпретировать, поэтому светлые головы придумали облегченные, но удобные для сравнения коэффициенты.
Среднее абсолютное отклонение (mean absolute deviation, MAD) определяется как частное от суммы остатков по модулю к числу наблюдений. То есть, средний остаток по модулю. Удобно? Вроде да, а вроде и не очень. В моем примере MAD=43. Выраженный в абсолютных единицах MAD показывает насколько единиц в среднем будет ошибаться прогноз.
MAPE призван придать модели еще более наглядный смысл. Расшифровывается выражение как средняя абсолютная ошибка в процентах (mean percentage absolute error, MAPE). 
где Y — значение исходного ряда.
Выражается MAPE в процентах, и в моем случае означает, что в модель может ошибаться в среднем на 16%. Что, согласитесь, вполне допустимо.
Наконец, последняя абсолютно синтетическая величина — это Bias, или просто смещение. Дело в том, что в реальном мире отклонения в одну сторону зачастую гораздо болезненнее, чем в другую. К примеру, при условно неограниченных складских помещениях, важнее учитывать скачки реального спроса вверх от спрогнозированных значений. Поэтому случаи, где остатки положительные относятся к общему числу наблюдений. В моем случае 44% спрогнозированных значений оказались ниже исходных. И можно пожертвовать другими критериями оценки, чтобы минимизировать этот Bias.
Можете попробовать это сами в 

Интересно узнать — какие методы оценки качества прогнозирования вы используете в своей работе?
Источник
Оценка точности и надежности прогнозов



Важным этапом прогнозирования социально-экономических явлений является оценка точности и надежности прогнозов.
Эмпирической мерой точности прогноза, служит величина его ошибки, которая определяется как разность между прогнозными ( 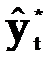
а) период упреждения известен, уже закончился, и исследователь располагает необходимыми фактическими значениями прогнозируемого показателя;
б) строится ретроспективный прогноз, то есть рассчитываются прогнозные значения показателя для периода времени, за который уже имеются фактические значения. Это делается с целью проверки разработанной методики прогнозирования.
В данном случае вся имеющаяся информация делится на две части в соотношении 2/3 к 1/3. Одна часть информации (первые 2/3 от исходного временного ряда) служит для оценивания параметров модели прогноза. Вторая часть информации (последняя 1/3 части исходного ряда) служит для реализации оценок прогноза.
Полученные таким образом ретроспективно ошибки прогноза в некоторой степени характеризуют точность предлагаемой и реализуемой методики прогнозирования. Однако величина ошибки ретроспективного прогноза не может в полной мере и окончательно характеризовать используемый метод прогнозирования, так как она рассчитана только для 2/3 имеющихся данных, а не по всему временному ряду.
В случае если, ретроспективное прогнозирование осуществляется по связным и многомерным динамическим рядам, то точность прогноза, соответственно, будет зависеть от точности определения значений факторных признаков, включенных в многофакторную динамическую модель, на всем периоде упреждения. При этом, возможны следующие подходы к прогнозированию по связным временным рядам: можно использовать как фактические, так и прогнозные значения признаков.
Все показатели оценки точности статистических прогнозов условно можно разделить на три группы:
Аналитические показатели точности прогнозапозволяют количественно определить величину ошибки прогноза. К ним относятся:
Абсолютная ошибка прогноза (D * ) определяется как разность между эмпирическими и прогнозными значениями признака и вычисляется по формуле:
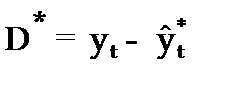
уt–фактическое значение признака;
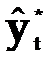
Относительная ошибка прогноза (d * отн) может быть определена как отношение абсолютной ошибки прогноза (D * ):
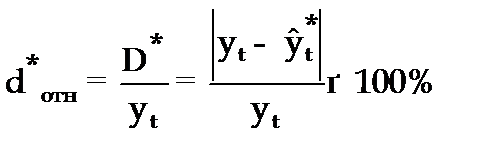
— к прогнозному значению признака ( 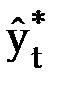
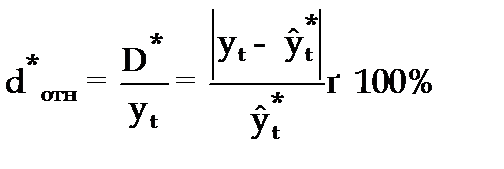
Абсолютная и относительная ошибки прогноза являются оценкой проверки точности единичного прогноза, что снижает их значимость в оценке точности всей прогнозной модели, так как изучаемое социально-экономическое явление подвержено влиянию различных факторов внешнего и внутреннего свойства. Единично удовлетворительный прогноз может быть получен и на базе реализации слабо обусловленной и недостаточно адекватной прогнозной модели и наоборот – можно получить большую ошибку прогноза по достаточно хорошо аппроксимирующей модели.
Поэтому на практике иногда определяют не ошибку прогноза, а некоторый коэффициент качества прогноза (Кк), который показывает соотношение между числом совпавших (с) и общим числом совпавших (с) и несовпавших (н) прогнозов и определяется по формуле:
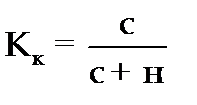
Значение Кк = 1 означает, что имеет место полное совпадение значений прогнозных и фактических значений и модель на 100% описывает изучаемое явление. Данный показатель оценивает удовлетворительный вес совпавших прогнозных значений в целом по временному ряду и изменяется в пределах от 0 до 1.
Следовательно, оценку точности получаемых прогнозных моделей целесообразно проводить по совокупности сопоставлений прогнозных и фактических значений изучаемых признаков.
Средним показателем точности прогнозаявляется средняя абсолютная ошибка прогноза ( 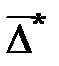
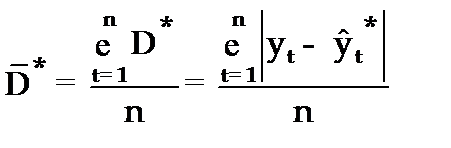
n–длина временного ряда.
Средняя абсолютная ошибка прогноза показывает обобщенную характеристику степени отклонения фактических и прогнозных значений признака и имеет ту же размерность, что и размерность изучаемого признака.

Для оценки точности прогноза используется средняя квадратическая ошибка прогноза, определяемая по формуле:
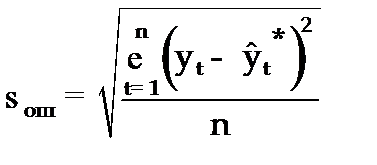
Размерность средней квадратической ошибки прогноза также соответствует размерности изучаемого признака. Между средней абсолютной и средней квадратической ошибками прогноза существует следующее примерное соотношение:
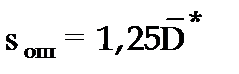
Недостатками средней абсолютной и средней квадратической ошибок прогноза является их существенная зависимость от масштаба измерения уровней изучаемых социально-экономических явлений.
Поэтому на практике в качестве характеристики точности прогноза определяют среднюю ошибку аппроксимации, которая выражается в процентах относительно фактических значений признака, и определяется по формуле вида:
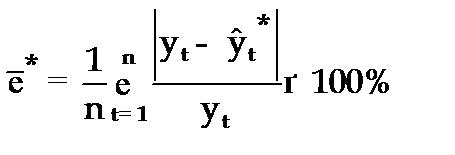
Данный показатель является относительным показателем точности прогноза и не отражает размерность изучаемых признаков, выражается в процентах и на практике используется для сравнения точности прогнозов полученных как по различным моделям, так и по различным объектам. Интерпретация оценки точности прогноза на основе данного показателя представлена в следующей таблице:
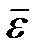 ,% ,% | Интерпретация точности |
| 50 | Высокая Хорошая Удовлетворительная Не удовлетворительная |
В качествесравнительного показателя точности прогнозаиспользуетсякоэффициент корреляции между прогнозными и фактическими значениями признака, который определяется по формуле:
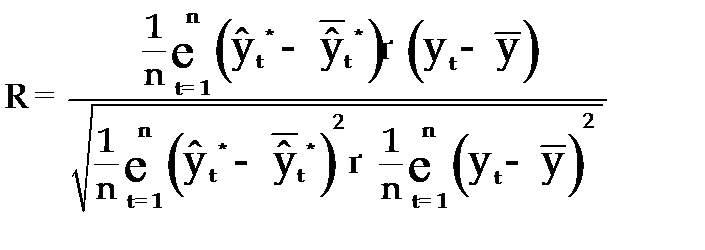
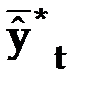
Используя данный коэффициент в оценке точности прогноза следует помнить, что коэффициент парной корреляции в силу своей сущности отражает линейное соотношение коррелируемых величин и характеризует лишь взаимосвязь между временным рядом фактических значений и рядом прогнозных значений признаков. И даже если коэффициент корреляции R = 1, то это еще не предполагает полного совпадения фактических и прогнозных оценок, а свидетельствует лишь о наличии линейной зависимости между временными рядами прогнозных и фактических значений признака.
Одним из показателей оценки точности статистических прогнозов является коэффициент несоответствия (КН), который был предложен Г. Тейлом и может рассчитываться в различных модификациях:
1. Коэффициент несоответствия (КН1), определяемый как отношение средней квадратической ошибки к квадрату фактических значений признака:
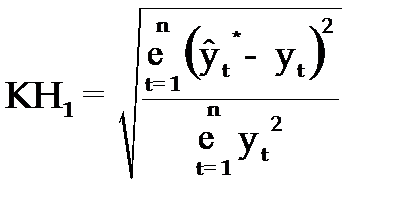
КН = 0, если 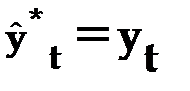
КН = 1, если при прогнозировании получают среднюю квадратическую ошибку адекватную по величине ошибке, полученной одним из простейших методов экстраполяции неизменности абсолютных цепных приростов.
КН > 1, когда прогноз дает худшие результаты, чем предположение о неизменности исследуемого явления. Верхней границы коэффициент несоответствия не имеет.
2.Коэффициент несоответствия (КН2), определяется как отношение средней квадратической ошибки прогноза к сумме квадратов отклонений фактических значений признака от среднего уровня исходного временного ряда за весь рассматриваемый период:
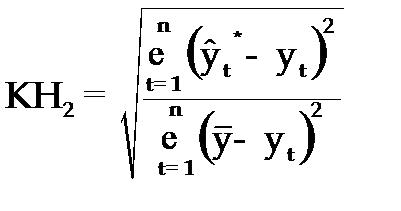
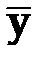
3.Коэффициент несоответствия (КН3), определяемый как отношение средней квадратической ошибки прогноза к сумме квадратов отклонений фактических значений признака от теоретических, выравненных по уравнению тренда:
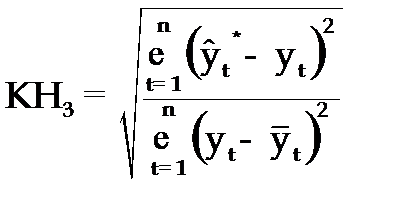
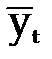
Контрольные вопросы к разделу III
1. Охарактеризуйте статистическое прогнозирование как составную часть общей теории прогностики.
2. Сформулируйте задачи статистического прогнозирования.
3. Дайте понятие объекта прогнозирования.
4. Перечислите основные понятия и термины, употребляемые в экономической прогностике.
5. Охарактеризуйте модели по сложности, масштабности и степени информационного обеспечения.
6. Раскройте содержание основных показателей точности прогнозов.
7. Раскройте сущность точечного и интервального прогнозов.
8. Как осуществляется предварительный анализ рядов динамики?
9. Раскройте содержание понятия объективизации прогнозов.
10. Перечислите простейшие методы прогнозирования динамики. Раскройте их сущность.
11. Охарактеризуйте метод прогнозирования на основе экстраполяции трендов.
12. Охарактеризуйте методы прогнозирования на основе кривых роста.
13. Охарактеризуйте метод простого экспоненциального сглаживания.
14. Охарактеризуйте метод гармонических весов.
15. Как достигается точность и надежность прогнозов на основе рядов динамики?
Источник

 Open Source Content Management
Open Source Content Management






