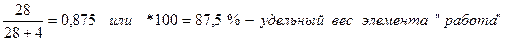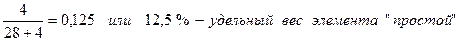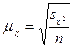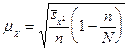Виды, способы и методы отбора единиц из генеральной в выборочную совокупность
Для того, чтобы выборка была репрезентативной, необходима объективная система организации отбора единиц из генеральной совокупности.
Различают два вида выборочного наблюдения или отбора единиц:
Повторный отбор («схема возвратного шара») предполагает, что отобранная однажды единица возвращается обратно в генеральную совокупность и имеет равную с другими единицами возможность быть отобранной вновь. Объём генеральной совокупности во время отбора остаётся неизменным.
Бесповторный отбор («схема безвозвратного шара») подразумевает, что однажды отобранная единица не возвращается в генеральную совокупность. Поэтому численность генеральной совокупности всё время уменьшается, а следовательно, вероятность попадания оставшихся единиц в выборку всё время возрастает. Бесповторный отбор даёт более точные результаты и поэтому на практике находит более широкое применение, чем повторный.
При проведении выборочного наблюдения могут использоваться следующие способы отбора единиц из генеральной совокупности:
— индивидуальный отбор – в выборку отбираются отдельные единицы исследуемой совокупности;
— групповой отбор – в выборку попадают качественно однородные группы или серии изучаемых единиц;
— комбинированный отбор предполагает комбинацию (сочетание) индивидуального и группового отбора.
Для формирования выборочной совокупности возможны следующие методы отбора единиц:
-комбинированные наблюдения (многоступенчатый отбор, многофазный отбор);
-моментно-выборочное наблюдение (метод моментных наблюдений).
Случайный (собственно-случайный) отбор предполагает равную вероятность попадания единиц в выборочную совокупность. Он может проводиться при помощи жеребьёвки или таблицы случайных чисел.
Механический отбор заключается в отборе единиц из генеральной совокупности, производимом в каком-либо механическом порядке (например, в отборе каждой 5-ой, каждой 10-й, 20-й и т.д. единицы). При этом для обеспечения репрезентативности выборки предполагается определённое расположение единиц генеральной совокупности (например, в алфавитном порядке либо в проранжированном по размеру признака виде и т.д.).
Промежуток, через который нужно отбирать единицы, или шаг отсчёта, зависит от пропорции отбора, исчисляемой делением численности генеральной совокупности на численность выборки:
Следовательно, например: 5-ая, 15-ая, 25-ая и т.д. (первая – любая из первых 10-и и далее + 10). Иногда первая – обязательно середина итога отсчёта (но это если было произведено предварительное ранжирование по исследуемому либо существенному признаку).
Типический отбор имеет место при изучении неоднородных по исследуемым признакам совокупностей. Тогда перед производством выборки генеральная совокупность делится на группы, а затем механическим либо случайным методом отбираются единицы. Обычно из каждой группы берется определенный процент единиц (пропорциональный отбор), но иногда и одинаковое число единиц (непропорциональный отбор).
Например, изучается уровень выполнения норм выработки. Известно, что на предприятии 80 % рабочих имеют высокую квалификацию и 20 % где низкую. Необходимо отобрать 120 человек, тогда:
120 *80 / 100 = 96 чел. – из группы высококвалифицированных рабочих.
120 * 20 / 100 = 24 чел. – из группы низкоквалифицированных рабочих.
Типический отбор иногда называют расслоенным, или стратифицированным. Он даёт более точные результаты по сравнению с другими методами отбора.
Серийный отбор предполагает отбор из генеральной совокупности не отдельных единиц, а групп, которые принято называть сериями (гнёздами). Внутри отобранных серий проводится сплошное обследование всех единиц.
Например, при проведении 20 % статистического контроля качества отбираются пачки (транспортные партии) изделий по 10 ед. Сменный выпуск составляет 250 изделий. Тогда число серий в генеральной совокупности:
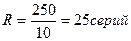
Число серий в выборочной совокупности можно определить двумя способами:
1) 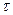
2) 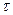
Серийный отбор легче организовать и провести, однако он имеет существенный недостаток: не обеспечивается представительство каждой серии, а следовательно, не исключается влияние межсерийной вариации.
Все рассматриваемые методы формирования выборочной совокупности предполагают отбор единиц совокупности в выборку уже на первом этапе отбора. Такой отбор называется одноступенчатым.
На практике часто используется многоступенчатый отбор, при котором на первом этапе отбираются группы (серии), а на следующем − механическим или случайным способом из отобранных серий выбираются единицы наблюдения. Учитывая, что при построении многоступенчатой выборки происходит комбинация различных методов отбора, такую выборку иногда называют комбинированной.
К комбинированной выборке относят и многофазный отбор. Его особенностью является тот факт, что из числа единиц, отобранных на первом этапе, на следующих этапах отбирается всё меньше единиц, но расширяется программа наблюдения.
Таблица 7.2 – Признаки, наблюдаемые по предприятиям, по этапам многофазного отбора
| № этапа | Количество наблюдаемых предприятий | Признаки |
| 1 этап | 1) объем продукции 2) число работающих 3) стоимость основных средств | |
| 2 этап | 1) объем продукции 2) число работающих 3) стоимость основных средств 4) фонд заработной платы 5) выручка от реализации продукции 6) прибыль 7) себестоимость | |
| 3 этап | 1) объем продукции 2) число работающих 3) стоимость основных средств 4) фонд заработной платы 5) выручка от реализации продукции 6) прибыль 7) себестоимость продукции 8) производительность труда 9) заработная плата 1 работающего 10)фондоотдача основных средств 11) затраты на 1 рубль продукции 12) рентабельность и т.д. |
Так как 1, 2, 3 признак повторяются на всех последующих этапах, аналогично далее повторяются 4, 5, 6, 7, это даёт возможность дополнительной проверки.
Основное отличие многофазного отбора от многоступенчатого состоит в том, что при многофазном отборе на каждом этапе единица отбора одна и та же, а при многоступенчатом − на каждом этапе своя единица отбора.
Особым методом выборочного наблюдения является метод моментных наблюдений (или моментно-выборочное наблюдение). Он используется достаточно широко в промышленности для изучения использования рабочего времени (исполнителей и оборудования).
Суть его заключается в том, что через определенные промежутки времени (в определенные моменты) происходит фиксация состояния изучаемой совокупности.
Например, оборудование – может быть зафиксировано два состояния: а) работа; б) простой.
За смену по единице оборудования А зафиксировано 28 элементов «работа» и 4 элемента «простой».
Следовательно,
Т.к. в смене 8 часов, или 480 минут, то оборудование работало (480*0,875) 420 минут, или 7 часов, и простаивало (480*0,125) 60 минут, или 1 час.
Особенность такой выборки: выборка производится по времени. Т.е. генеральная совокупность – продолжительность смены, выборочная совокупность – совокупность отдельных моментных состояний объекта.
Дата добавления: 2016-01-16 ; просмотров: 5825 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
Способы отбора единиц из генеральной совокупности



В статистике применяются различные способы формирования выборочных совокупностей, что обусловливается задачами исследования и зависит от специфики объекта изучения.
Основным условием проведения выборочного обследования является предупреждение возникновения систематических ошибок, возникающих вследствие нарушения принципа равных возможностей попадания в выборку каждой единицы генеральной совокупности. Предупреждение систематических ошибок достигается в результате применения научно обоснованных способов формирования выборочной совокупности.
Существуют следующие способы отбора единиц из генеральной совокупности:
1) индивидуальный отбор — в выборку отбираются отдельные единицы;
2) групповой отбор — в выборку попадают качественно однородные группы или серии изучаемых единиц;
3) комбинированный отбор — это комбинация индивидуального и группового отбора.
Способы отбора определяются правилами формирования выборочной совокупности.
Выборка может быть:
Собственно-случайная выборка состоит в том, что выборочная совокупность образуется в результате случайного (непреднамеренного) отбора отдельных единиц из генеральной совокупности. При этом количество отобранных в выборочную совокупность единиц обычно определяется исходя из принятой доли выборки.
Доля выборки есть отношение числа единиц выборочной совокупности n к численности единиц генеральной совокупности N, т.е.
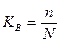
Так, при 5%-ной выборке из партии товара в 2 000 ед. численность выборки n составляет 100 ед. (5*2000:100), а при 20%-ной выборке она составит 400 ед. (20*2000:100) и т.д.
Механическая выборка состоит в том, что отбор единиц в выборочную совокупность производится из генеральной совокупности, разбитой на равные интервалы (группы). При этом размер интервала в генеральной совокупности равен обратной величине доли выборки.
Так, при 2%-ной выборке отбирается каждая 50-я единица (1:0,02), при 5%-ной выборке — каждая 20-я единица (1:0,05) и т.д.
Таким образом, в соответствии с принятой долей отбора, генеральная совокупность как бы механически разбивается на равновеликие группы. Из каждой группы в выборку отбирается лишь одна единица.
Важной особенностью механической выборки является то, что формирование выборочной совокупности можно осуществить, не прибегая к составлению списков. На практике часто используют тот порядок, в котором фактически размещаются единицы генеральной совокупности. Например, последовательность выхода готовых изделий с конвейера или поточной линии, порядок размещения единиц партии товара при хранении, транспортировке, реализации и т.д.
Типическая выборка.При типической выборке генеральная совокупность вначале расчленяется на однородные типические группы. Затем из каждой типической группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность.
Типическая выборка обычно применяется при изучении сложных статистических совокупностей. Например, при выборочном обследовании производительности труда работников торговли, состоящих из отдельных групп по квалификации.
Важной особенностью типической выборки является то, что она дает более точные результаты по сравнению с другими способами отбора единиц в выборочную совокупность.
Для определения средней ошибки типической выборки используются формулы:
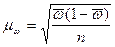
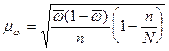
Дисперсия определяется по следующим формулам:
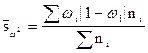
При одноступенчатой выборке каждая отобранная единица сразу же подвергается изучению по заданному признаку. Так обстоит дело при собственно-случайной и серийной выборке.
При многоступенчатой выборке производят подбор из генеральной совокупности отдельных групп, а из групп выбираются отдельные единицы. Так производится типическая выборка с механическим способом отбора единиц в выборочную совокупность.
Комбинированная выборка может быть двухступенчатой. При этом генеральная совокупность сначала разбивается на группы. Затем производят отбор групп, а внутри последних осуществляется отбор отдельных единиц.

Тема 7: Статистическое изучение динамики
7.1 Понятие о рядах динамики
7.2 Правила построения рядов динамики
7.3 Показатели анализа ряда динамики
7.4 Методы анализа основной тенденции развития в рядах динамики
7.5 Методы изучения сезонных колебаний
7.6 Экстраполяция в рядах динамики и прогнозирование
Основная цель статистического изучения динамики коммерческой деятельности состоит в выявлении и измерении закономерностей их развития во времени. Это достигается посредством построения и анализа статистических рядов динамики.
Рядами динамики называются статистические данные, отображающие развитие изучаемого явления во времени. В каждом ряду динамики имеются два основных элемента: показатель времени t; соответствующие им уровни развития изучаемого явления у. В качестве показаний времени в рядах динамики выступают либо определенные даты (моменты) времени, либо отдельные периоды (годы, кварталы, месяцы, сутки).
Уровни рядов динамики отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или средними величинами.
В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам. В соответствии с этим, ряды динамики подразделяются на моментные и интервальные.
Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени.
Особенностью моментного ряда динамики является то, что в его уровни могут входить одни и те же единицы изучаемой совокупности. Так, основная часть персонала фирмы N, составляющая списочную численность на 1.01.1994г., продолжающая работать в течение данного года, отображена в уровнях последующих периодов. Поэтому при суммировании уровней моментного ряда динамики может возникнуть повторный счет.
Интервальные ряды динамики отображают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени.
Особенностью интервального ряда динамики является то, что каждый его уровень складывается из данных за более короткие интервалы времени. Например, суммируя товарооборот за первые три месяца года, получают его объем за I квартал, а сумма товарооборота четырех кварталов дает объем товарооборота за год и т.д.
Источник