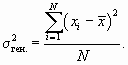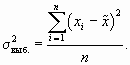Способы организации выборочных наблюдений

Раздел 1. Теория статистики

Цель: сформировать представление о способах решения задач, которые возникают при использовании выборочного наблюдения.

Задачи: познакомить студентов с методикой различных видов статистического наблюдения, оценки надежности выборочных показателей с учетом их случайной ошибки

Оглавление

4.1. Особенности выборочного наблюдения. Генеральная и выборочная совокупности

Выборочное наблюдение – это вид несплошного наблюдения, которое обеспечивает отбор в случайном порядке части единиц совокупности и возможность последующего распространения полученных данных на всю совокупность единиц.

Исходный массив данных называется генеральной совокупностью. Часть единиц генеральной совокупности, которая непосредственно обследуется при выборочном наблюдении, представляет собой выборочную совокупность. Числовые характеристики генеральной совокупности (средняя, дисперсия и др.) называются параметрами генеральной совокупности.

Организационными вопросами выборочного наблюдения являются: обоснование границ генеральной совокупности; единица отбора; единица наблюдения; способы отбора.

4.2. Виды и способы отбора. Виды выборочного наблюдения

По способу организации различают следующие основные виды выборочного наблюдения: собственно-случайная (простая) выборка; типическая (расслоенная, стратифицированная, районированная); серийная (гнездовая); многоступенчатая; многофазная.

При любом виде выборки отбор единиц производится тремя способами: случайный отбор (жеребьевка, таблица случайных чисел); отбор единиц по какой-либо схеме (единицы упорядочивают таким образом, чтобы это было не связано с изучаемыми свойствами; далее проводится механический отбор единиц); сочетание первого и второго способов.

Простая собственно-случайная выборка проводится из всей массы единиц совокупности без предварительного разделения ее на какие-либо группы. Применяется индивидуальный отбор единиц, т. е. единица отбора совпадает с единицей наблюдения. Типическая, (районированная, стратифицированная) выборка используется в случае, когда генеральная совокупность неоднородна и это влияет на размер изучаемого признака. Серийная выборка (кластерный или гнездовой отбор) – это способ формирования выборки, при котором единица отбора состоит из группы или гнезда более мелких единиц, называемых элементами. Многоступенчатая выборка применяется, когда имеют место несколько стадий отбора (ступеней отбора). При этом каждая стадия имеет свою единицу отбора. Число ступеней отбора определяется числом типов единиц отбора и на последней ступени единица отбора совпадает с единицей выборочной совокупности. Многофазная выборка характеризуется тем, что она также включает несколько ступеней отбора, но на всех ступенях сохраняется одна и та же единица отбора (в отличие от многоступенчатой).

Особым видом выборочного наблюдения является моментное наблюдение – это выборочное во времени наблюдение. Объектом выборки являются отрезки времени. Поэтому понятие генеральной и выборочной совокупности относится не к совокупности единиц, а ко времени наблюдения.

4.3. Определение ошибки выборочного наблюдения. Средняя и предельная ошибки выборочного наблюдения

Расхождение между значениями показателей, полученных по выборке, и соответствующими параметрами генеральной совокупности называется ошибкой репрезентативности. Различают систематические и случайные ошибки выборки. Случайные ошибки выборки объясняются недостаточно равномерным представлением в выборочной совокупности различных категорий единиц генеральной совокупности. Систематические ошибки могут быть связаны с нарушением правил отбора или условий реализации выборки.

Величина случайной ошибки репрезентативности зависит от ряда факторов: объема выборки; степени вариации изучаемого признака в генеральной совокупности; принятого способа формирования выборочной совокупности.

Различают среднюю (стандартную) и предельную ошибку выборки. Средняя ошибка выборки характеризует меру отклонений выборочных показателей от аналогичных показателей генеральной совокупности. Предельной ошибкой выборки принято считать максимально возможное расхождение выборочной и генеральной характеристик, т. е. максимум ошибки при заданной вероятности ее появления. Соотношение между пределом ошибки выборки , гарантируемым с некоторой вероятностью Р(t), и средней ошибкой выборки имеет вид: или , где t – коэффициент доверия, определяемый в зависимости от уровня вероятности Р(t). Наряду с абсолютной величиной предельной ошибки выборки рассчитывается и относительная ошибка выборки, которая определяется как процентное отношение предельной ошибки выборки к соответствующей характе ристике выборочной совокупности. На практике величина дисперсии признака в генеральной совокупности, как правило, неизвестна, поэтому в формулы ошибки выборки подставляют дисперсию выборочной совокупности.

Выборочная дисперсия несколько меньше генеральной, в математической статистике доказано, что

Если выборочная совокупность большого объема (то есть n достаточно велико), то соотношение приближается к единице и выборочная дисперсия практически совпадает с генеральной.

Выборку считают безусловно большой, если n>100.

Источник

Выборочное наблюдение в статистике

Понятие и виды выборочного наблюдения

Выборочное наблюдение применяется, когда применение сплошного наблюдения физически невозможно из-за большого массива данных или экономически нецелесообразно. Физическая невозможность имеет место, например, при изучении пассажиропотоков, рыночных цен, семейных бюджетов. Экономическая нецелесообразность имеет место при оценке качества товаров, связанной с их уничтожением, например, дегустация, испытание кирпичей на прочность и т.п.

Статистические единицы, отобранные для наблюдения, составляют выборочную совокупность или выборку, а весь их массив — генеральную совокупность (ГС). При этом число единиц в выборке обозначают n, а во всей ГС — N. Отношение n/N называется относительный размер или доля выборки.

Качество результатов выборочного наблюдения зависит от репрезентативности выборки, то есть от того, насколько она представительна в ГС. Для обеспечения репрезентативности выборки необходимо соблюдать принцип случайности отбора единиц, который предполагает, что на включение единицы ГС в выборку не может повлиять какой-либо иной фактор кроме случая.

Существует 4 способа случайного отбора в выборку:

Собственно случайный отбор или «метод лото», когда статистическим величинам присваиваются порядковые номера, заносимые на определенные предметы (например, бочонки), которые затем перемешиваются в некоторой емкости (например, в мешке) и выбираются наугад. На практике этот способ осуществляют с помощью генератора случайных чисел или математических таблиц случайных чисел.

Механический отбор, согласно которому отбирается каждая (N/n)-я величина генеральной совокупности. Например, если она содержит 100 000 величин, а требуется выбрать 1 000, то в выборку попадет каждая 100 000 / 1000 = 100-я величина. Причем, если они не ранжированы, то первая выбирается наугад из первой сотни, а номера других будут на сотню больше. Например, если первой оказалась единица № 19, то следующей должна быть № 119, затем № 219, затем № 319 и т.д. Если единицы генеральной совокупности ранжированы, то первой выбирается № 50, затем № 150, затем № 250 и так далее.

Отбор величин из неоднородного массива данных ведется стратифицированным (расслоенным) способом, когда генеральная совокупность предварительно разбивается на однородные группы, к которым применяется случайный или механический отбор.

Особый способ составления выборки представляет собой серийный отбор, при котором случайно или механически выбирают не отдельные величины, а их серии (последовательности с какого-то номера по какой-то подряд), внутри которых ведут сплошное наблюдение.

Качество выборочных наблюдений зависит и от типа выборки: повторная или бесповторная.
При повторном отборе попавшие в выборку статистические величины или их серии после использования возвращаются в генеральную совокупность, имея шанс попасть в новую выборку. При этом у всех величин генеральной совокупности одинаковая вероятность включения в выборку.
Бесповторный отбор означает, что попавшие в выборку статистические величины или их серии после использования не возвращаются в генеральную совокупность, а потому для остальных величин последней повышается вероятность попадания в следующую выборку.

Бесповторный отбор дает более точные результаты, поэтому применяется чаще. Но есть ситуации, когда его применить нельзя (изучение пассажиропотоков, потребительского спроса и т.п.) и тогда ведется повторный отбор.

Ошибки выборки

Выборочную совокупность можно сформировать по количественному признаку статистических величин, а также по альтернативному или атрибутивному. В первом случае обобщающей характеристикой выборки служит выборочная средняя величина, обозначаемая , а во втором — выборочная доля величин, обозначаемая w. В генеральной совокупности соответственно: генеральная средняя и генеральная доля р.

Разности — и W — р называются ошибкой выборки, которая делится на ошибку регистрации и ошибку репрезентативности. Первая часть ошибки выборки возникает из-за неправильных или неточных сведений по причинам непонимания существа вопроса, невнимательности регистратора при заполнении анкет, формуляров и т.п. Она достаточно легко обнаруживается и устраняется. Вторая часть ошибки возникает из-за постоянного или спонтанного несоблюдения принципа случайности отбора. Ее трудно обнаружить и устранить, она гораздо больше первой и потому ей уделяется основное внимание.

Величина ошибки выборки может быть разной для разных выборок из одной генеральной совокупности, поэтому в статистике определяется средняя ошибка повторной и бесповторной выборки по формулам:

— повторная;

— бесповторная;

где Дв — выборочная дисперсия.

Например, на заводе с численностью работников 1000 чел. проведена 5%-ая случайная бесповторная выборка с целью определения среднего стажа работников. Результаты выборочного наблюдения приведены в первых двух столбцах следующей таблицы:

X, лет
(стаж работы)

f, чел.
(число работников в выборке)

Xиf

Источник

Выборочное наблюдение в статистике

11.1. Основные положения теории выборочного метода наблюдения

Суть выборочного метода заключается в отборе отдельных единиц обследуемой совокупности по специальным правилам, гарантирующим реализацию принципа случайности отбора, с целью получения обобщающих статистических характеристик изучаемой совокупности.

Выборочный метод позволяет получать достоверные результаты лишь тогда, когда соблюдается принцип равновозможности каждой единицы быть отобранной. При этом только случай, а не какой-либо иной фактор, влияет на решение включить рассматриваемую единицу в выборочную совокупность или нет. Из всех методов несплошного наблюдения выборочный считается наиболее теоретически разработанным. Положенный в его основу принцип случайности позволяет математически обосновать дальнейшее распространение выборочных характеристик на всю совокупность.

Выборочная совокупность репрезентативна (представительна) в том случае, если она верно отражает закономерности, структуру генеральной совокупности.

Широкое применение выборочного метода в статистической практике объясняется рядом его преимуществ по сравнению со сплошным наблюдением. Основными являются:

• быстрота получения результатов обследования. Существенное уменьшение объема наблюдения за счет отбора лишь части единиц совокупности позволяет быстрее собрать информацию и оперативнее получить сводные результаты обследования;
• значительное снижение затрат, непосредственно связанных с проведением наблюдения. При использовании выборки затраты уменьшаются за счет сокращения количества обследуемых единиц наблюдения;
• возможность расширения программы наблюдения. Уменьшение количества наблюдаемых единиц позволяет изучить их детальнее, используя более широкий перечень вопросов;
• возможность использования в тех случаях, когда проведение сплошного наблюдения методологически невозможно. Например, при статистических исследованиях качества продукции либо когда генеральная совокупность объектов бесконечно велика и нет возможности обследовать каждую единицу (при маркетинговых обследованиях покупателей, изучении пассажиропотоков и т.д.).

Вместе с тем выборочный метод имеет ряд недостатков. Важнейший из них связан с наличием ошибок репрезентативности, которые обусловлены тем, что наблюдаются не все единицы изучаемой совокупности. Кроме того, его проведение требует привлечения высококвалифицированного персонала, что в свою очередь ведет к увеличению стоимости обследования.

11.1.1. Основные определения и обозначения

В теории выборочного наблюдения используются специфические понятия, определения и обозначения.

Под термином генеральная совокупность понимается изучаемая статистическая совокупность, из которой проводится отбор единиц для непосредственного наблюдения (количество единиц генеральной совокупности обозначается через N).

Отобранная по определенным правилам часть единиц генеральной совокупности образует выборочную совокупность (n — количество единиц выборочной совокупности).

Доля выборочной совокупности в общем объеме генеральной совокупности, выраженная в процентах, называется долей отбора (процентом выборки, процентом отбора):

Например, при объеме генеральной совокупности в 200 единиц и выборочной — в 50 единиц говорят о 25%-ной выборке (доля отбора — 25%).

Если исследуется количественный признак, то непосредственная задача выборочного наблюдения — это оценка среднего и суммарного значения признака. Среднее значение признака в генеральной совокупности принято обозначать через x. По данным генеральной совокупности оно может быть определено как

Среднее значение признака в выборочной совокупности обозначается через x. Оно исчисляется как

Дисперсия единиц количественного признака определяется следующим образом:

Так как генеральная дисперсия по большей части в ходе исследования остается неизвестной, то условно принимают ее равной дисперсии, рассчитываемой по выборочным данным;

Наряду с нахождением характеристик количественных признаков могут оцениваться характеристики альтернативных показателей.

Обозначая численность единиц, обладающих изучаемым признаком, в генеральной совокупности через М, а в выборочной — через m, получим долю единиц, обладающих исследуемым признаком в генеральной совокупности: p = M/N и в выборочной: w = m/n.

Дисперсия альтернативного признака рассчитывается следующим образом:

Основной целью статистического наблюдения является получение достоверной статистической информации. Но при любом способе наблюдения могут возникнуть погрешности, которые приведут к снижению качества получаемой информации. Эти погрешности называются ошибками наблюдения. При сплошном наблюдении возможны только ошибки регистрации (случайные и систематические). При выборочном наблюдении возможны как ошибки регистрации, так и ошибки репрезентативности. Те и другие могут носить как случайный, так и систематический характер.

Задача выборочного наблюдения состоит в измерении случайной ошибки репрезентативности, которая возникает вследствие несплошного характера наблюдения при любом способе отбора.

11.1.2. Основные этапы работ при организации выборочного наблюдения

К основным этапам работ при организации выборочного наблюдения относятся:

• постановка цели и определение задач выборочного наблюдения в соответствии с экономической задачей исследования;
• разработка программы наблюдения;
• проектирование бланков анкет, создание инструкции по проведению наблюдения и заполнению статистических формуляров;
• решение организационных вопросов наблюдения, в том числе подготовка квалифицированного персонала;
• определение состава единиц генеральной совокупности;
• выбор способа формирования выборочной совокупности, решение вопросов, связанных с определением доли отбора, объема выборки и размера допустимой ошибки наблюдения;
• сбор данных (регистрация исследуемых признаков у отобранных единиц наблюдения);
• получение характеристик выборочной совокупности;
• определение ошибок выборки;
• распространение результатов выборки на изучаемую cовокупность;
• выводы и рекомендации на основе полученных результатов выборочного наблюдения.

11.1.3. Роль закона больших чисел при определении ошибок выборочного наблюдения

Центральное место в теории выборочного наблюдения занимает задача оценки репрезентативности выборочной совокупности. Ошибки репрезентативности представляют собой отклонения характеристик выборочной совокупности от характеристик генеральной.

Теория оценивания ошибок выборки базируется на ряде предельных теорем под общим названием «закон больших чисел». В них доказывается, что ошибки могут быть сведены к минимальным значениям. При этом возможно установить их значения с требуемой точностью.

Так, в приложении к выборочному методу из теоремы Чебышева следует, что с вероятностью, сколь угодно близкой к единице, можно утверждать, что при достаточно большом объеме выборки, полученной с соблюдением всех правил ее формирования, разность между генеральной и выборочной средними будет сколь угодно мала. Теорема Ляпунова позволяет оценить предельную ошибку выборки для среднего значения признака. Теорема Бернулли является частным случаем теоремы Чебышева применительно к исследованию доли альтернативного признака.

11.1.4. Способы отбора единиц в выборочную совокупность. Классификация видов выборочного наблюдения

Различают индивидуальный, групповой и комбинированный отбор.

При индивидуальном отборе в выборочную совокупность отбираются отдельные единицы генеральной совокупности, например при обследованиях промышленности — предприятия, при обследованиях населения — конкретные люди и т.д. Индивидуальный отбор применяется при организации собственно случайной, механической, типической выборок.

При групповом отборе единицы отбираются группами; ими могут быть, например, бригады, микрорайоны (этот вид отбора свойственен для серийной выборки).

Комбинированный отбор предполагает сочетание индивидуального и группового отбора, например, сначала отбираются группы единиц (групповой отбор), а затем из них случайным образом — конкретные единицы (индивидуальный отбор). В этом случае выборка также называется комбинированной.

Кроме того, каждый из перечисленных способов отбора может быть бесповторным или повторным.

Бесповторным является такой отбор, в результате которого однажды отобранная в выборку единица наблюдения не может быть отобранной из генеральной совокупности во второй раз. При повторном отборе попавшая в выборку единица наблюдения вновь возвращается в совокупность, и ее можно отобрать во второй, третий раз и т.д.

В статистике встречаются разнообразные виды выборок: собственно-случайная выборка, механическая, типическая, серийная, комбинированная. Свои особенности имеет малая выборка.

Вид выборки определяется задачами исследования, полнотой и особенностями информации, которой мы располагаем об объекте наблюдения.

Собственно-случайная выборка. Отбор единиц при использовании собственно случайной выборки производится путем жеребьевки или с использованием таблицы случайных чисел. При этом все единицы совокупности должны иметь равные шансы попасть в выборочную совокупность.

Для отбора единиц наблюдения путем жеребьевки подготавливаются определенные жребии: шары или карточки (могут применяться и другие виды жребиев), содержащие ссылки на конкретную единицу генеральной совокупности — ее номер, если совокупность пронумерована, адрес и т.д. Жребии перемешивают и в случайном порядке отбирают n штук, ровно столько, сколько единиц должно быть отобрано в выборочную совокупность. Этот способ хорош, если количество объектов генеральной совокупности невелико и имеется возможность на каждый из них завести жребий. Но на практике чаще всего работают с большими совокупностями — порядка десятков или сотен тысяч единиц. Тогда прибегают к помощи таблиц случайных чисел.

Таблица случайных чисел представляет собой набор колонок случайных цифр. Случайность сочетания определяется отсутствием закона их расположения и приблизительно равной частотой встречаемости каждой из десяти цифр при образовании случайного числа.

Существует множество методов составления таблиц случайных чисел. В наше время они генерируются с помощью датчика случайных чисел. Его содержат все современные статистические пакеты прикладных программ, а также Excel, входящий в набор стандартных программ для Windows.

Пример 11.1. Предположим нужно отобрать 15 студентов из 200, обучающихся на первом курсе, методом случайной бесповторной выборки.

Таблица 11.1. Фрагмент таблицы случайных чисел

Ряд		01	02	03	04	05	06
Колонка	1	66194	78240	00833	12111	47189	76396
2	28926	43195	88000	86683	99951	72486
Ряд		07	08	09	10	11	12
Колонка	1	46409	74626	34450	36327	74185	12296
2	17469	22111	81974	72135	77536	41623
Ряд		13	14	15	16	17	18
Колонка	1	60822	72121	95268	92603	18813	38840
2	60280	79152	41377	09091	90291	26903
Ряд		19	20	21	22	23	24
Колонка	1	05959	85141	75047	30752	22986	99439
2	33836	21155	59643	95260	82575	86692
Ряд		25	26	27	28	29	30
Колонка	1	20389	39249	96777	04860	41613	17930
2	93029	05173	33605	32918	42375	00794
Ряд		31	32	33
Колонка	1	24649	79899	76801
2	31845	34061	49594

Проведем отбор с помощью таблицы случайных чисел следующим образом:

1. пронумеруем единицы изучаемой совокупности, т.д. присвоим каждому студенту индивидуальный номер, начиная с 001, 002, и т.д. до 200.
2. из таблицы случайных чисел выберем любой ее фрагмент, например первые два столбца;
3. поскольку объем выборки составляет 15 студентов, нам нужно отобрать в случайном порядке 15 трехзначных чисел из приведенного фрагмента. Так как индивидуальные номера, присвоенные студентам, являются трехзначными, а в рассматриваемой таблице содержатся пятизначные комбинации цифр, мы будет рассматривать только три, например, последние цифры в каждой комбинации, начиная с первой из выбранного фрагмента. При этом трехзначное число не должно превышать 200 (т.е. индивидуального номера последнего студента в списке). Следуя этим правилам, мы должны выписать число 194, пропускаем числа 240 и 833, поскольку они больше 200, затем выпишем 111, 189 и т.д. до 173 (т.е. 15 чисел) (в табл. эти числа выделены).

Среди выписанных чисел число 111 встречается дважды, а по условию отбор должен быть случайным бесповторным. Поэтому одно из этих чисел пропустим и запишем следующее после 173 подходящее по условию число — это число 061.

В итоге получим следующие числа:

194, 111, 189, 185, 121, 141, 047,

195, 135, 152, 091, 155, 029, 173, 061.

В выборочную совокупность должны быть включены студенты, индивидуальные номера которых в исходном списке соответствуют отобранным числам. Таким образом, в выборку попали студенты, имеющие следующие номера в списке:

029, 047, 061, 091, 111, 121, 135,

141, 152, 155, 173, 185, 189, 194, 195.

Механическая выборка. Наряду со случайным отбором в практике выборочного наблюдения применяется механический отбор. При этом все единицы генеральной совокупности нумеруются числами от 1 до N, после чего отбирается каждая (N/n)-я единица для обследования. Величина N/n называется шагом, или интервалом, отбора.

Если список единиц в генеральной совокупности составлен в порядке возрастания изучаемого признака, указанный подход может привести к систематической ошибке: начиная отбор с первой единицы из этого интервала получим заниженную оценку генеральной средней, если начать с последней — завышенную. Поэтому целесообразно выбрать начальную точку отсчета (отбора) случайным образом, а затем производить отбор в соответствии с рассчитанным шагом отбора.

Допустим, надо отобрать 50 студентов из 200, обучающихся на первом курсе, методом механической выборки. Для этого необходимо сделать следующее:

1. Определим шаг отбора: N/n = 200/50 = 4 (следовательно, необходимо отбирать одного студента из каждых четырех). Порядковый номер, с которого должен начаться отбор, может быть таким: или 1-й, или 2-й, или 3-й или 4-й студент.
2. Определим точку начала отбора по выбранному фрагменту из таблицы случайных чисел. Для этого выберем любой столбец цифр, соответствующий разряду шага отбора (в нашем случае — первому разряду), например последнюю колонку во втором столбце: 6, 5, 0, 3, 1, 6… Следовательно, порядковый номер, с которого должен начаться отбор, равен 3 (это первое число из выписанных, которое нам подходит).
3. Теперь будем отбирать студентов по списку, начиная с 3-го, с шагом, равным 4: 3-го, 7-го, 11-го, 15-го студента и т.д.

Типическая выборка. В случае использования типической выборки cовокупность предварительно разбивается на однородные типы или группы, а затем производится случайный (или механический) отбор единиц наблюдения внутри полученных групп. Извлеченная подобным образом выборка будет типической (в литературе она также называется расслоенной, стратифицированной, районированной).

Типическая выборка в статистической практике применяется гораздо чаще, чем остальные виды выборочного наблюдения. Так, при обследованиях населения в зависимости от целей исследования генеральную совокупность расслаивают по возрастному или социальному признаку, типу проживания (городское, сельское населения и т.д.); при обследованиях малых предприятий типизация осуществляется по четырем признакам: территориальному, отраслевому, виду собственности и размеру выручки. Этим достигается однородность единиц внутри групп. Типическая выборка дает более точные результаты.

Серийная (гнездовая) выборка. Если генеральную совокупность можно разделить на одинаковые по объему и однородные группы, то целесообразно осуществлять отбор не единиц, а их серий. После такого отбора внутри серий проводится сплошное обследование.

Например, при оценке качества продукции можно отбирать партии товара, а затем обследовать все входящие в них изделия; при некоторых обследованиях населения отбираются в порядке серий жилые дома, в которых опрашиваются жильцы всех квартир; обследования школьников проводятся путем отбора однотипных школ или конкретных классов, ученики которых подвергаются сплошному опросу, и т.д.

Комбинированные выборки. Комбинированный отбор широко применяется на практике и представляет собой сочетание разных методов отбора (их комбинацию), например типического с механическим. В этом случае генеральная совокупность разбивается на типические группы на основе ранее выбранного группировочного признака, внутри этих групп единицы наблюдения упорядочиваются, устанавливается шаг отбора, соответствующий необходимой численности выборки, после чего происходит извлечение единиц наблюдения из типических групп на основе механического отбора. Подобная комбинация методов обеспечивает представительство в выборке всех типов единиц наблюдения (за счет применения типического отбора) и сохраняет структуру типических групп по группировочным признакам, обеспечиваемую механическим отбором.

Малая выборка. Выборка считается малой, если количество объектов, отобранных для выборочного наблюдения, не превышает 20 единиц.

Малые выборки используются в тех ситуациях, когда распределение признака в генеральной совокупности является нормальным или приближается к нему. Только в этих случаях построенные доверительные интервалы или рассчитанные доверительные вероятности будут иметь реальное практическое значение.

Источник