otvety / 11Способы организации параллельной обработки информации
Общий метод увеличения производительности – организация параллельной обработки информации, т. е. одновременное решение задач или совмещение во времени этапов решения одной задачи.
Способы организации. Во всем многообразии способов организации параллельной обработки можно выделить три основных направления: • совмещение во времени различных этапов разных задач; • одновременное решение различных задач пли частей одной задачи; • конвейерная обработка информации.
Первый путь – совмещение во времени этапов решения разных задач – это мультипрограммная обработка информации. Мультипрограммная обработка возможна даже в однопроцессорной ЭВМ и широко используется в современных СОД. Второй путь – одновременное решение различных задач или частей одной задачи – возможен только при наличии нескольких обрабатывающих устройств. При этом используются те или иные особенности задач или потоков задач, что позволяет осуществить тот или иной параллелизм. Можно выделить несколько типов параллелизма, отражающих эти особенности.
Типы параллелизма: 1. Естественный параллелизм независимых задач заключается в том, что в систему поступает непрерывный поток не связанных между собой задач, т. е. решение любой задачи не зависит от результатов решения других задач. В этом случае использование нескольких обрабатывающих устройств при любом способе комплексирования (косвенном или прямом) повышает производительность системы. 2. Параллелизм независимых ветвей – один из наиболее распространенных типов параллелизма в обработке информации. Суть его заключается в том, что при решении большой задачи могут быть выделены отдельные независимые части – ветви программы, которые при наличии нескольких обрабатывающих устройств могут выполняться параллельно и независимо друг от друга. Двумя независимыми ветвями программы будем считать такие части задачи, при выполнении которых выполняются следующие условия: 1. ни одна из входных для ветви программы величин не является выходной величиной другой программы (отсутствие функциональных связей); 2. для обеих ветвей программы не должна производиться запись в одни и те же ячейки памяти (отсутствие связи по использованию одних и тех же полей оперативной памяти); 3. условия выполнения одной ветви не зависят от результатов или признаков, полученных при выполнении другой ветви (независимость по управлению); 4. обе ветви должны выполняться по разным блокам программы (программная независимость). 3. Параллелизм объектов или данных имеет место тогда, когда по одной и той же (или почти по одной и той же) программе должна обрабатываться некоторая совокупность данных, поступающих в систему одновременно. Это могут быть, например, задачи обработки сигналов от радиолокационной станции: все сигналы обрабатываются по одной и той же программе. Другой пример – обработка информации от датчиков, измеряющих одновременно один и тот же параметр и установленных на нескольких однотипных объектах. Программы обработки данных могут быть различного объема и сложности, начиная от очень простых, содержащих несколько операций, до больших программ в сотни и тысячи операций.
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Источник
Организация параллельной обработки информации
Общий метод увеличения производительности – организация параллельной обработки информации, т. е. одновременное решение задач или совмещение во времени этапов решения одной задачи.
Способы организации. Во всем многообразии способов организации параллельной обработки можно выделить три основных направления:
1) совмещение во времени различных этапов разных задач;
2) одновременное решение различных задач или частей одной задачи;
3) конвейерная обработка информации.
Первый путь – совмещение во времени этапов решения разных задач – это мультипрограммная обработка информации. Мультипрограммная обработка возможна даже в однопроцессорной ЭВМ.
Второй путь – одновременное решение различных задач или частей одной задачи – возможен только при наличии нескольких обрабатывающих устройств. При этом используются те или иные особенности задач или потоков задач, что позволяет осуществить тот или иной параллелизм. Можно выделить несколько типов параллелизма, отражающих эти особенности.
Естественный параллелизм независимых задач заключается в том, что в систему поступает непрерывный поток не связанных между собой задач, т. е. решение любой задачи не зависит от результатов решения других задач. В этом случае использование нескольких обрабатывающих устройств при любом способе комплексирования (косвенном или прямом) повышает производительность системы.
Параллелизм независимых ветвей – один из наиболее распространенных типов параллелизма в обработке информации. Суть его заключается в том, что при решении большой задачи могут быть выделены отдельные независимые части – ветви программы, которые при наличии нескольких обрабатывающих устройств могут выполняться параллельно и независимо друг от друга. Двумя независимыми ветвями программы будем считать такие части задачи, при выполнении которых выполняются следующие условия:
ни одна из входных для ветви программы величин не является выходной величиной другой программы (отсутствие функциональных связей);
для обеих ветвей программы не должна производиться запись в одни и те же ячейки памяти (отсутствие связи по использованию одних и тех же полей оперативной памяти);
условия выполнения одной ветви не зависят от результатов или признаков, полученных при выполнении другой ветви (независимость по управлению);
обе ветви должны выполняться по разным блокам программы (программная независимость).
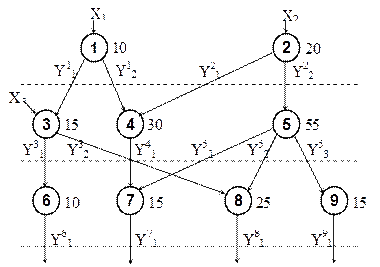
Хорошее представление о параллелизме независимых ветвей дает ярусно-параллельная форма программы, пример которой приведен на рис. 2.1. Программа представлена в виде совокупности ветвей, расположенных в нескольких уровнях – ярусах. Кружками с цифрами внутри обозначены ветви. Длина ветви представляется цифрой, стоящей около кружка. Стрелками показаны входные данные и результаты обработки. Входные данные обозначаются символом х, выходные данные – символом у. Символы х имеют нижние цифровые индексы, означающие номера входных величин; символы у имеют цифровые индексы и внизу и вверху; цифра вверху соответствует номеру ветви, при выполнении которой получен данный результат, а цифра внизу означает порядковый номер результата, полученного при реализации данной ветви программы.
Рис. 2.1. Ярусно-параллельная форма программы
Изображенная на рисунке программа содержит 14 ветвей, расположенных на 5 ярусах. Ветви каждого яруса не связаны друг с другом, т. е. результаты решения какой-либо ветви данного яруса не являются входными данными для другой ветви этого же яруса. На этом же графе могут быть изображены и связи по управлению или памяти. В этом случае граф позволяет наглядно показать полностью независимые ветви. Для простоты изображения мы этого не делаем.
На примере этой, в общем достаточно простой программы, можно выявить преимущества вычислительной системы, включающей несколько обрабатывающих устройств, и проблемы, которые при этом возникают.
Примем, что длина i-й ветви представляется числом временных единиц ti, которые требуются для ее исполнения. Тогда нетрудно подсчитать, что для исполнения всей программы потребуется единиц времени. Если представить, что программа выполняется двумя обрабатывающими устройствами, работающими независимо друг от друга, то время решения задачи сократится. Однако это время, как нетрудно видеть, будет различным в зависимости от последовательности выполнения независимых ветвей.
Для того чтобы с помощью нескольких обрабатывающих устройств решить задачу, имеющую независимые параллельные ветви, необходима соответствующая организация процесса, которая определяет пути решения задачи и вырабатывает необходимую информацию о готовности каждой ветви. Заметим, что все это относительно легко реализовать тогда, когда известна достаточно точно длительность выполнения каждой ветви, На практике это бывает крайне редко: в лучшем случае известна приближенная длина ветвей. Поэтому организация оптимального или близкого к оптимальному графика работы является достаточно сложной задачей.
Заметим, что, как правило, трудно избежать некоторых простоев, которые возникают из-за отсутствия исходных данных для выполнения той или иной ветви. Все это приводит в конечном счете к тому, что выигрыш в производительности системы несколько снижается. Следует отметить также и определенные сложности, связанные с выделением независимых ветвей при разработке программ. Вместе с тем при решении многих сложных задач только программирование с выделением независимых ветвей позволяет существенно сократить время решения.
Параллелизм объектов или данных имеет место тогда, когда по одной и той же (или почти по одной и той же) программе должна обрабатываться некоторая совокупность данных, поступающих в систему одновременно.
Это могут быть, например, задачи обработки сигналов от радиолокационной станции: все сигналы обрабатываются по одной и той же программе. Другой пример – обработка информации от датчиков, измеряющих одновременно один и тот же параметр и установленных на нескольких однотипных объектах. Программы обработки данных могут быть различного объема и сложности, начиная от очень простых, содержащих несколько операций, до больших программ в сотни и тысячи операций.
Это могут быть и чисто математические задачи, например задачи векторной алгебры – операции над векторами и матрицами, характеризующиеся некоторой совокупностью чисел. Решение задачи при этом в значительной степени сводится к выполнению одинаковых операций над парами чисел двух аналогичных объектов. Так, например, сложение двух матриц размерностью заключается в сложении соответствующих элементов этих матриц. При этом операция сложения должна быть проведена над парами чисел. Произведение матрицы размерностью на скаляр сводится к выполнению умножений элементов матрицы на скаляр: и т. д. Очевидно, все эти операции могут выполняться параллельно и независимо друг от друга несколькими обрабатывающими устройствами.
Третий путь параллельной обработки информации – конвейерная обработка – может быть реализован в системе и с одним процессором, разделенным на некоторое число последовательно включенных операционных блоков, каждый из которых специализирован на выполнении строго определенной части операции.(Принцип работы конвейера был рассмотрен при изучении МП.)
Напомним, работу конвейера для обработки данных можно представить следующей схемой.
Процессор работает таким образом: когда i-й операционный блок выполняет i-о часть j-й операции, (i–1)-й операционный блок выполняет (i–1)-ю часть (j+1)-й операции, а (i+1)-и операционный блок выполняет (i+1)-ю часть (j–1)-й операции. В результате образуется своего рода конвейер обработки, который хорошо может быть проиллюстрирован следующим простым примером.
Рис. 2.2. Структурная схема конвейера операций
Операцию сложения двух чисел с плавающей запятой 
можно разделить на четыре последовательно исполняемых этапа, или шага: сравнение порядков (СП); выравнивание порядков – сдвиг мантиссы с меньшим порядком для выравнивания с мантиссой с большим порядком (ВП); сложение мантисс (СМ); нормализация результата (НР). В соответствии с этим в составе процессора предусмотрены четыре операционных блока, соединенных последовательно и реализующих четыре вышеперечисленных шага операции сложения: блоки СП, ВП, СМ и НР (рис. 2.2). Примем, что время выполнения каждого шага равно соответственно 60, 100, 140, 100 нс. Таким образом, операция сложения будет выполняться последовательностью операционных блоков за время 400 нс.
Далее предположим, что возникает задача сложения двух векторов А и В, содержащих по и элементов с плавающей запятой. Очевидно, для решения этой задачи потребуется сложить два числа: 
Выполним эти операции на процессоре, организовав обработку данных следующим образом. После того как блок СП выполнит свою часть операции над первой парой операндов, он передает результат в следующий блок – ВП, а в блок СП будет загружена очередная пара операндов. На следующем шаге блок ВП передает результат выполнения своей части операции в блок СМ и начнет обрабатывать вторую пару операндов и т. д. Для того чтобы не создавались очереди операндов на обработку, примем, что время выполнения каждого из этих этапов одинаково и равно максимальному значению нс. В результате получим конвейер из четырех операционных блоков. Первый результат на выходе конвейера будет получен через 140X4 = 560 нс, т. е. несколько позже, чем если бы время выполнения всех этапов не выравнивалось. Однако все последующие результаты будут выдаваться через каждые 140 нc.
На рис. 2.2, б представлена временная диаграмма процесса. Общее время сложения двух векторов с помощью описанного конвейера , где т – число операционных блоков. Если бы конвейер не использовался, то это время было бы равно где – время выполнения i-го этапа обработки. Если применить конвейерную обработку к векторам, состоящим из 25 элементов, то получим ТК= (25 + 4– 1) • 140 = 3920 нc, Т0 = 25 • 400 = 10 000 нс.
Нетрудно заметить, что чем длиннее цепочка данных и чем на большее число этапов (а следовательно, и операционных блоков) разбивается операция (при той же длительности ее выполнения), тем больший эффект от использования конвейера может быть получен.
В приведенном выше примере было рассмотрено конвейерное выполнение арифметических операций, но идея конвейера может быть распространена и на выполнение команд. Надо сказать, что конвейер команд применяется уже давно в обычных ЭВМ.
Источник
Типы параллельной обработки информации
Под термином параллельная обработка мы будем понимать одновременное выполнение заданий, шагов (пунктов) заданий, программ, подпрограмм, циклов, операторов и команд. Параллельная обработка информации может применяться с двумя основными целями:
1. Повышение производительности ЭВМ и ВС не за счет совершенствования элементной базы, а за счет эффективной организации вычислительных процессов.
2. Обеспечение высокой надежности ВС за счет дублирования вычислительной аппаратуры.
Рис. 5.1. Уровни параллелизма
Повышение производительности ЭВМ и ВС – основная цель применения параллельной обработки, по этой причине параллельную архитектуру имеют такие ЭВМ, как многопроцессорные серверы, мэйнфреймы и супер-ЭВМ.
Параллельная обработка информации может производиться на нескольких уровнях (рис. 5.1).
Очевидно, что чем ниже уровень, тем мельче дробление программных процессов, тем мельче, как принято говорить, «зерно параллелизма». В общем случае возможно реализовать параллелизм как на отдельном уровне, так и на нескольких одновременно. Независимая однопроцессорная обработка реализует параллелизм на уровне 1. Векторная обработка заключается в параллельном выполнении циклов на уровне 2 и может производиться как на одном, так и нескольких процессорах. Уровни 3 и 4 соответствуют многопроцессорным ВС. Параллелизм уровня 5 характерен для многомашинных вычислительных комплексов.
Существует два основных способа организации параллельной обработки:
· совмещение во времени этапов решения разных задач;
· одновременное решение различных задач или частей одной задачи;
Первый путь — совмещение во времени этапов решения разных задач — это мультипрограммная обработка информации. Мультипрограммная обработка уже давно и широко применяется для повышения производительности ЭВМ и ВС. Подробное рассмотрение мультипрограммной обработки относится к теме «Операционные системы» и выходит за рамки настоящего учебника.
Второй путь — одновременное решение различных задач или частей одной задачи — возможен только при наличии нескольких обрабатывающих устройств. При этом используются те или иные особенности задач или потоков задач, что позволяет осуществить распараллеливание.
Можно выделить следующие типы параллелизма, позволяющие реализовать алгоритмические особенности отдельных задач и их потоков.
1. Естественный параллелизм независимых задач.
2. Параллелизм объектов или данных.
3. Параллелизм ветвей задачи или программы.
Рассмотрим эти типы параллелизма.
1. Естественный параллелизм независимых задач заключается в том, что на вход ВС поступает непрерывный поток не связанных между собой задач, т.е. решение любой задачи не зависит от результатов решения других задач. В этом случае использование нескольких обрабатывающих устройств при любом способе комплексирования (объединения в систему) повышает производительность системы.
Характерным примером естественного параллелизма является поступление пользовательских запросов на информационный web-сайт. Каждый запрос порождает отдельную процедуру его исполнения, которая не зависит от других подобных процедур.
2. Параллелизм объектов или данных имеет место тогда, когда по одной и той же (или почти по одной и той же) программе должна обрабатываться некоторая совокупность данных, поступающих в систему одновременно.
Это могут быть, например, задачи обработки сигналов от радиолокационной станции: все сигналы обрабатываются по одной и той же программе. Другой пример — обработка информации от датчиков, измеряющих одновременно один и тот же параметр и установленных на нескольких однотипных объектах.
Программы подобного типа могут быть различного объема и сложности, начиная от очень простых, содержащих несколько операций, до больших программ в сотни и тысячи операций. При этом параллельность выполнения операций достигается путем увеличения числа обрабатывающих устройств, каждое из которых способно автономно выполнять последовательность команд над отдельной совокупностью данных. Часто основной особенностью таких программ (в частности программ обработки векторов и матриц) является то, что одна и та же команда должна выполняться над большой совокупностью элементарных, связанных между собой некоторым образом данных, и соответствующую операцию можно производить над всеми данными одновременно. При этом время решения задачи сокращается пропорционально числу обрабатывающих устройств.
3. Параллелизм ветвей задачи или программы — один из наиболее распространенных типов параллелизма в обработке информации. Он заключается в том, что при решении одной задачи могут быть выделены отдельные ее части — ветви, которые при наличии нескольких обрабатывающих устройств могут выполняться параллельно. При этом одновременно могут обрабатываться только независимые ветви задачи, т.е. такие ее части, для которых соблюдаются следующие условия:
· ни одна из выходных величин этих ветвей задачи не является входной величиной для другой такой ветви (отсутствие функциональных связей);
· условия выполнения одной ветви не зависят от результатов или признаков, полученных при выполнении других ветвей (независимость по управлению).
Хорошее представление о параллелизме ветвей дает ярусно-параллельная форма(ЯПФ) программы, пример которой приведен на рис. 5.2.
Программа представлена в виде совокупности ветвей, расположенных на нескольких уровнях — ярусах. Кружками с цифрами внутри обозначены ветви. Длина ветви представляется цифрой, стоящей около кружка и говорящей, сколько временных единиц выполняется данная ветвь. Стрелками показаны входные данные и результаты обработки. Входные данные обозначаются символом X, выходные данные — символом Y. Символы Х имеют нижние цифровые индексы, обозначающие номера входных величин; символы Y имеют цифровые индексы и внизу, и вверху; цифра вверху соответствует номеру ветви, при выполнении которой получен данный результат, а цифра внизу означает порядковый номер результата, полученного при реализации данной ветви программы. На одном ярусе размещаются независимые ветви задачи, не связанные друг с другом, т.е. результаты решения какой-либо ветви данного яруса не являются входными данными для другой ветви этого же яруса.
Рис. 5.2. Пример ярусно-параллельной формы программы
Изображенная на рис. 5.2 программа содержит 9 ветвей, расположенных на 3 ярусах. На примере этой, в общем, достаточно простой программы, можно выявить преимущества вычислительной системы, включающей несколько обрабатывающих устройств, и проблемы, которые при этом возникают.
Примем, что длина i-й ветви представляется числом временных единиц ti, которые требуются для ее исполнения. Тогда нетрудно подсчитать, что для исполнения всей программы на 1 процессоре потребуется время T1:
T1=S (10+20+15+30+55+10+15+25+15)=195
Если представить, что программа выполняется двумя обрабатывающими устройствами (процессорами), работающими независимо друг от друга, то время решения задачи сократится. Однако, это время, как нетрудно видеть, будет различным в зависимости от последовательности выполнения независимых ветвей.
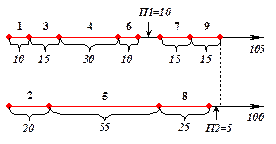
Рассмотрим, например, такой вариант выполнения программы, представленной на рис. 5.2. Пусть процессор 1 выполняет ветви 1-3-4-6-7-9, а процессор 2 выполняет ветви 2-5-8. На рис. 5.3 представлены временные диаграммы выполнения процессорами ветвей программы.
Рис. 5.3. Разложение ветвей программы по 2 процессорам
Нетрудно подсчитать, что процессор 1 затрачивает 105, а процессор 2 — 100 единиц времени. При этом имеется два промежутка времени, когда один из процессоров вынужденно простаивает – П1 длительностью 10 единиц и П2 длительностью 5 единиц времени. Промежуток П1, во время которого работает только процессор 2, образовался из-за того, что ветвь 7 зависит от ветви 5 (к моменту завершения ветви 6 еще не готовы данные Y 5 1). Промежуток П1, во время которого работает только процессор 1, образовался по причине окончания счета процессором 2.
Таким образом, на системе из двух процессоров наша программа будет выполнена полностью не менее, чем за 105 единиц времени. Величину, характеризующую уменьшение времени решения задачи на нескольких процессорах по сравнению с использованием одного процессора, называют ускорением счета S и рассчитывают как
 , | (5.1) |
где TP – время решения задачи на p процессорах. Кроме ускорения, используют такую величину, как коэффициент распараллеливания Kп, который рассчитывается как
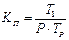 | (5.2) |
Коэффициент распараллеливанияизменяется от 0 до 1 (от 0 до 100%) и отражает эффективность использования вычислительных ресурсов. В нашем примере нетрудно посчитать, что ускорение S= 195/105 = 1,86, а коэффициент распараллеливания Kп = 0,93. Как видим, по причине простоев одного из процессоров ускорение счета значительно меньше 2, т.е. количества используемых процессоров. Заметим, что в нашем примере не учитывались временные задержки, связанные с переключением контекстов программы (смены ветвей) и передачи данных от одной ветви к другой. Тем не менее, в силу алгоритмических особенностей программы, часть вычислений в промежутки П1 и П2 производится только одним процессором, т.е. фактически последовательно.
Рассмотрим обобщенный случай программы, в которой алгоритмически доля последовательных вычислений (отношение времени последовательных вычислений к общему времени счета программы) составляет некоторую величину f. В этом случае время выполнения программы на системе из p процессоров не может быть меньше величины
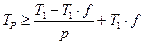 | (5.3) |
Первое слагаемое определяет время выполнения распараллеленной части программы, а второе слагаемое – время выполнения последовательной части программы. Нетрудно видеть, что ускорение счета в этом случае не будет превышать величины
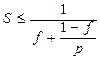 | (5.4) |
Данное соотношение носит название закона Амдала. На примере программы рис. 5.2 мы можем видеть, что доля последовательных вычислений составляет f= 15/195. Подставляя эту величину в формулу закона Амдала, получаем для системы из двух процессоров максимальное ускорение 1,86 раза, что соответствует ранее рассчитанному значению.
Для иллюстрации действия закона Амдала приведем следующий пример. Пусть доля последовательных вычислений в некоторой программе составляет 10%. Тогда максимальное ускорение счета на 100 процессорах не превысит 9,2. Коэффициент распараллеливания составит всего лишь 9,2%. На 10 процессорах ускорение составит 5,3, а коэффициент распараллеливания ‑ 53%. Нетрудно видеть, что даже такая небольшая доля последовательных вычислений уже на теоретическом уровне, без учета неизбежных задержек в реальной ВС, серьезно ограничивает возможности масштабирования программы.
Определим, какая должна быть максимальная доля f последовательных вычислений в программе, чтобы было возможно получить наперед заданное ускорение счета S с максимальным коэффициентом распараллеливания Kп. Для этого выразим из закона Амдала долю последовательных вычислений:
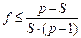 | (5.5) |
Из соотношения (5.5) видно, что для того, чтобы допустить наличие последовательных вычислений в программе (fдолжно быть больше 0), число процессоров p должно быть больше предполагаемого ускорения S. При этом условии максимальный коэффициент распараллеливания Kп получается при числе процессоров p = S+1. Таким образом, доля последовательных вычислений должна составлять не более
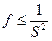 | (5.6) |
Соотношение (5.6) определяет очень важное следствиеиз закона Амдала. Для того, чтобы ускорить программу в q раз, необходимо ускорить не менее, чем в q раз не менее, чем ( 
)-ю часть программы. Например, чтобы получить ускорение в 100 раз, необходимо распараллелить 99,99% всей программы.
Кроме алгоритмического распараллеливания, для того, чтобы с помощью нескольких обрабатывающих устройств решить задачу, имеющую параллельные ветви, необходима соответствующая организация процесса, которая определяет пути решения задачи и вырабатывает необходимую информацию о готовности каждой ветви. Однако все это относительно легко реализовать тогда, когда известна достаточно точно длительность выполнения каждой ветви. На практике это бывает крайне редко: в лучшем случае имеется та или иная временная оценка. Поэтому организация оптимального или близкого к оптимальному графика работы является достаточно сложной задачей.
Следует отметить также и определенные сложности, связанные с выделением независимых ветвей при разработке программ. Вместе с тем при решении многих сложных задач только программирование с выделением независимых ветвей позволяет существенно сократить время решения. В частности, хорошо поддаются параллельной обработке такого типа задачи матричной алгебры, линейного программирования, спектральной обработки сигналов, прямые и обратные преобразования Фурье и др.
Источник
