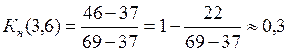Способы оптимизации сетевых графиков производства работ

Оптимизация сетевого графика

Оптимизация сетевого графика проводится по времени и ресурсам. Цель оптимизации по времени – сократить продолжительность критического пути. Цель оптимизации по ресурсам – выровнять загрузку исполнителей и сократить численность занятых.

На практике оптимизация сетевого графика проводится чаще всего по времени, чтобы сократить продолжительность разработки в целом, или уложиться в установленные сроки. При этом надо учитывать коэффициенты напряженности путей. Работы, лежащие на путях с коэффициентом напряженности , уже могут быть использованы для оптимизации сетевого графика, при этом в первую очередь, используются резервы работ с путей, имеющих минимальные коэффициенты напряженности.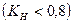

Оптимизация сетевого графика проводится:

– путем изменения схемы сетевого графика, в частности, разделение продолжительной работы на несколько работ, выполняемых параллельно;

– путем перевода части исполнителей с ненапряженных работ, то есть имеющих частные резервы времени, на работы критического пути, выполняемые параллельно с ненапряженными работами. При переводе исполнителей должны быть учтены их квалификация и специальность;

– путем изменения сроков начала и окончания работ ненапряженных путей в пределах их полного резерва времени.

Оптимизация сетевого графика включает следующие этапы:

1. Определяется объем ненапряженной работы (чел-дней), с которой предполагается перевести часть исполнителей на работу критического пути по формуле:

, (10.3.11.)

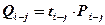
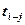
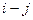
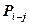
где – продолжительность работы в днях;

– количество исполнителей на данной работе.

2. Определяется оптимальная численность исполнителей для выполнения данной работы при условии увеличения ее продолжительности на величину частного резерва времени по формуле:

, (10.3.12.)

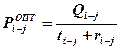
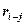
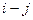
где – частный резерв времени работы.

3. Определяется количество исполнителей, которые могут быть переведены на параллельно выполняемую работу критического пути по формуле:

. (10.3.13.)

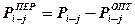
4. Определяется объем работы критического пути, на которую предполагается перевести часть исполнителей, по формуле:

. (10.3.14.)

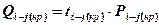
5. Определяется продолжительность работы критического пути после увеличения численности исполнителей на этой работе, по формуле:

. (10.3.15.)

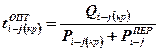
6. Определяется продолжительность критического пути после оптимизации сетевого графика.

Пример. Разработать и оптимизировать сетевой график по технологической подготовке производства нового изделия, согласно приведенным данным в табл. 10.3.1.

Оптимизация сетевого графика

№	Наименование работ	Код работы	Продолжительность работы, дни	Количество исполнителей	Специальность
1.	Отработка конструкции на технологичность	1-2	Технолог
2.	Разработка технологии кузнечно-штамповочного производства	2-3	Технолог
3.	Разработка технологии литейного производства	2-4	Технолог
4.	Разработка технологии механической обработки	2-5	Технолог
5.	Разработка технологии сборки	3-4	Технолог
6.	Проектирование кузнечной оснастки	3-6	Конструктор
7.	Проектирование литейной оснастки	4-6	Конструктор
8.	Фиктивная работа	5-6	–
9.	Проектирование оснастки для механической обработки	6-7	Конструктор

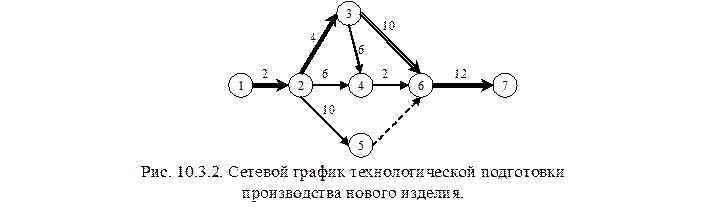
По приведенным данным строится сетевой график технологической подготовки производства (рис. 10.3.2.).

Расчет основных параметров сетевого графика сводим в таблицу 10.3.2.

Расчет основных параметров сетевого графика

№	Код работы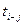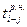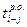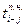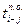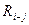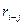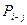
1-2
2-3
2-4
2-5
3-4
3-6
4-6
5-6
6-7

Длина критического пути составит:

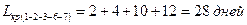
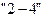
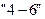
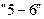
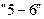
Частными резервами времени располагают работы: , , . Работа является фиктивной, поэтому для оптимизации сетевого графика не принимается.

Продолжительность пути, по которому проходят работы, имеющие частные резервы времени, составит:

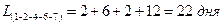
Коэффициент напряженности для данного пути составит:

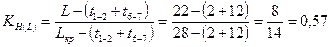
Так как коэффициент напряженности 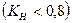, то ресурсы данных работ можно использовать для оптимизации сетевого графика.

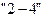
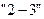
Наибольшим резервом времени имеет работа , с которой можно перевести часть исполнителей на работу критического пути, выполняемую параллельно, то есть на работу .

Оптимизацию сетевого графика проводим в следующей последовательности:

1. Определяем объем работы :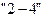

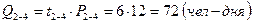
2. Определяем оптимальную численность исполнителей на данной работе:

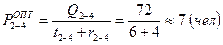
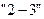
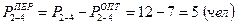
3. Определяем количество исполнителей, которых можно перевести на работу критического пути:

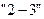
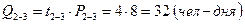
4. Определяем объем работы на критическом пути:

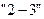
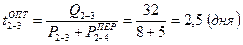
5. Определяем продолжительность работы после увеличения численности исполнителей на ней:

6. Определяем продолжительность критического пути после оптимизации сетевого графика:

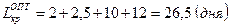
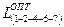
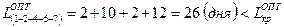
Проверяем продолжительность пути после оптимизации:

Коэффициент напряженности работ данного пути после оптимизации составит:

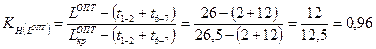
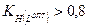
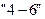
Так как , то использовать резерв времени работы , лежащей на данном пути, для дальнейшей оптимизации сетевого графика нецелесообразно.

Таким образом, проведя оптимизацию сетевого графика, продолжительность технологической подготовки производства нового изделия сократилась с 28 до 26,5 дня, т. е. на 1,5 дня.

Источник

Методы оптимизации сетевого графика

После того как сетевой график построен и рассчитаны его основные параметры, приступают к его оптимизации. Оптимизация сетевого графика может заключаться либо в сокращении продолжительности критического пути, либо в сокращении ресурсов, необходимых для выполнения всего комплекса работ сетевого графика без изменения его продолжительности.

Вначале рассмотрим анализ и оптимизацию календарных сетей, т.е. тех, в которых заданы только оценки продолжительности работ.

Анализ сетевого графика начинается с анализа топологии сети, включающего контроль построения сетевого графика, установление целесообразности выбора работ, степени их расчленения.

Затем проводятся классификация и группировка работ по величинам резервов. Необходимо отметить, что величина полного резерва времени далеко не всегда может достаточно точно характеризовать, насколько напряженным является выполнение той или иной работы некритического пути. Все зависит от того, на какую последовательность работ распространяется вычисленный резерв, какова продолжительность этой последовательности.

Оценить степень трудности своевременного выполнения всех работ, а также отдельных «цепочек» пути можно с помощью коэффициента напряженности работ.

Коэффициентом напряженности К_н работы (i, j) называется отношение продолжительности несовпадающих (заключенных между одними и теми же событиями) отрезков пути, одним из которых является путь максимальной продолжительности, проходящий через данную работу, а другим – критический путь.

Коэффициент напряженности вычисляется по следующей формуле:

, (5.10)

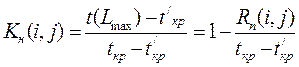
где t (L_max) — продолжительность максимального пути, проходящего через работу (i,j);

t_кр – продолжительность критического пути;

t / _кр — продолжительность отрезка рассматриваемого пути, совпадающего с критическим путем;

R_п (i, j) – полный резерв времени работы (i, j).

Коэффициент напряженности изменяется от нуля (для работ, у которых отрезки максимального из путей, не совпадающие с критическим путем, состоят из фиктивных работ нулевой продолжительности) до единицы (для работ критического пути). Причем, чем ближе он к единице, тем сложнее выполнить данную работу в установленный срок.

Найдем коэффициент напряженности работы (3,6) для сетевого графика (рис. 5.2). Ранее мы установили, что продолжительность критического пути t_кр = 69 (суток). Далее необходимо определить продолжительность максимального пути (отличного от критического), проходящего через работу (3,6). Такой путь включает в себя события 1 → 2 → 3 → 6 → 7 → 8 → 9 → 10 → 11 → 12 и имеет продолжительность t (L_max) = 46 (суток). Максимальный путь совпадает с критическим на отрезке 6 → 7 → 8 → 9 → 10 → 11 → 12 продолжительностью t / _кр = 4 + 4 + 2 + 10 + 12 + 5 = 37 (суток). Используя формулу (5.10), получим

В соответствии со значениями коэффициента напряженности все работы сетевого графика можно разделить на три группы:

— подкритические (0,6

2) изменения топологии сети в результате внедрения новой технологии производства работ, позволяющей находить новые последовательности и взаимосвязи работ;

3) расчленения длительных работ на отдельные части и замены последовательных работ параллельными.

Перераспределение ресурсов как инструмент оптимизации сетевого графика предполагает перемещение между работами как трудовых ресурсов, так и техники. При перераспределении трудовых ресурсов необходимо соблюдать ряд правил, в частности: 1) работы, по которым осуществляется перераспределение, должны выполняться в один и тот же период времени; 2) перераспределять ресурсы возможно только на равнокачественных работах, т.е. таких, которые требуют работников одной и той же или взаимозаменяемой профессии и квалификации; 3) перераспределять ресурсы необходимо по величине их убывания в работы с наибольшим дефицитом ресурсов.

В процессе сокращения продолжительности работ критический путь может измениться и в дальнейшем процесс оптимизации будет направлен на сокращение продолжительности работ нового критического пути. И так будет продолжаться до получения удовлетворительного результата. В идеале длина любого из полных путей может стать равной длине критического пути или, по крайней мере, пути критической зоны. Тогда все работы будут вестись с равным напряжением, а срок завершения проекта существенно сократится.

До сих пор мы говорили лишь о соблюдении плановых сроков выполнения комплекса работ, не затрагивая вопросов стоимости разработки проектов. Однако на практике при попытках эффективного улучшения составленного плана неизбежно введение дополнительного к оценкам сроков фактора стоимости работ. Поэтому далее рассмотрим оптимизацию сетевого графика методом «время/стоимость».

Оптимизация сетевого графика в зависимости от полноты решаемых задач может быть условно разделена на частную и комплексную. Разновидностями частной оптимизации сетевого графика являются: минимизация времени выполнения комплекса работ при заданной его стоимости; минимизация стоимости комплекса работ при заданном времени выполнения проекта.

Комплексная оптимизация представляет собой нахождение оптимального соотношения величин стоимости и сроков выполнения проекта в зависимости от конкретных целей, ставящихся при его реализации.

При использовании метода «время-стоимость» предполагают, что уменьшение продолжительности работы пропорционально возрастанию ее стоимости. Каждая работа (i, j) характеризуется продолжительностью t (i, j), которая может находиться в пределах

a (i, j) ≤ t (i, j) ≤ b (i, j), (5.11)

где b (i, j) – нормальная продолжительность выполнения работы (i, j); a (i, j) – минимально возможная (экстренная) продолжительность работы (i, j), которую только можно осуществить в условиях разработки.

При этом стоимость с (i, j) работы (i, j) заключена в границах от с_min (i, j) (при нормальной продолжительности работы) до с_max (i, j) (при экстренной продолжительности работы).

Используя аппроксимацию по прямой (рис. 5.6), можно легко найти изменение стоимости работы ∆с (i, j) при сокращении ее продолжительности на величину

∆с (i, j) = [ b (i, j) – t (i, j)]h (i, j). (5.12)

Величина h (i, j), равная тангенсу угла α наклона аппроксимирующей прямой, показывает затраты на ускорение работы (i, j) (по сравнению с нормальной продолжительностью) на единицу времени:

. (5.13)

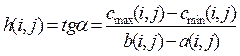
Самый очевидный вариант частной оптимизации сетевого графика с учетом стоимости предполагает использование резервов времени работ. Продолжительность каждой работы, имеющей резерв времени, увеличивают до тех пор, пока не будет исчерпан этот резерв или пока не будет достигнуто верхнее значение продолжительности b (i, j). При этом стоимость выполнения проекта, равная до оптимизации

(5.14)

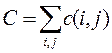
уменьшается на величину

. (5.15)

c_max (i,j)

c (i,j)

Δc (i,j)

Продолжитель-ность работы

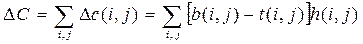
c_min (i,j)

Рис. 5.6. Зависимость стоимости работы от ее продолжительности

После сокращения критического пути за счет проведениятех или иных мероприятий необходимо заново пересчитать сетевой график, чтобы выявить достаточность принятых мер и проверить, не появились ли новые критические пути.

Источник