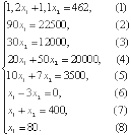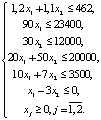Способы оптимизации показателей экономико математические методы

Использование математических методов способствовало зарождению экономической науки. Применение математики к экономике обеспечило исследование и объяснение изменения спроса и предложения, рыночного равновесия, построения производственной функции и т.д. Математика на макроуровне обеспечивает решение задач выбора монетарной политики, формирования антициклической политики, прогнозирования экономического роста, занятости, объемов внешней торговли и изменения мировых рынков. На микроуровне математика решает задачи оценки и предсказания изменения спроса, предложения, поведения потребителей, оказывающихся под влиянием различных факторов, но наибольшую ценность математика несет в ее применении в организации производства. Вопрос выбора направления хозяйственной деятельности является наиболее важным для предприятия, поскольку оно всегда стремится максимизировать прибыль, а следовательно, снизить затраты и увеличить выручку. Данной цели можно достичь, применяя математические инструменты в поиске оптимальной производственной политики, обеспечивающей максимальную прибыль [1, с. 936].

Целью исследования является изучение практики применения экономико-математических методов в решении задачи оптимизации производственных процессов, снижения затрат и максимизации прибыли.

Объектом исследования выступают производственно-экономические отношения, возникающие в процессе планирования хозяйственной деятельности, оптимизации производственных процессов, сокращения затрат и максимизации прибыли хозяйствующих субъектов.

Материалы и методы исследования

В исследовании производилась оптимизация производства двух видов напитков с использованием графического метода линейного программирования, также рассматривался случай его применения для целочисленного линейного программирования. Наглядная интерпретация исходных и полученных в ходе работы данных была произведена в табличной и графической форме.

Материалы исследования были сформированы на основе работ отечественных и зарубежных ученых, опубликованных в ведущих рецензируемых изданиях из перечней ВАК и включаемых в международные базы данных, а также на основе учебно-методических работ.

Результаты исследования и их обсуждение

Рассмотрим простой, но реальный экономический процесс. Например, имеется фирма, которая выпускает 2 вида напитков: пиво и квас. Для изготовления пива используются 4 исходных продукта: вода, солодовый концентрат, сахар, дрожжи. Для изготовления кваса используются 4 исходных продукта: вода, хлебный концентрат, сахар, дрожжи. Сырье следует подбирать таким образом, чтобы оно использовалось и для одного, и для другого продуктов, в данном случае общими ресурсами являются вода, сахар и дрожжи. Также возможны случаи использования определенного сырья только для одного из конечных продуктов производства: так, для пива требуется солодовый, а для кваса – хлебный концентрат.

Следующий момент, на который нужно обратить внимание, – это количественные данные, т.е. расходы исходных продуктов на 1 л продукции и суточные запасы (табл. 1).

Исходные данные модели (начальное условие)

Кроме требований к запасам сырья, могут предъявляться и иные. Например, в связи с проведением чемпионата мира по футболу суточный спрос на пиво превышает спрос на квас, однако не более чем в 3 раза. Кроме того, установлено, что спрос на пиво не превышает 80 л за сутки. Для упаковки продукции фирма использует пластиковые бутылки объемом 1 л и в день может использовать не более 400 бутылок.

Обычно бывают два основных вопроса: составить оптимальный план производства продукции либо с наибольшей прибылью, либо с наименьшими затратами. Выбираем наибольшую прибыль, однако не хватает данных о цене продукции, значит, их следует добавить [2, с. 45].

Розничная цена за 1 л пива составляет 100 рублей, за 1 л кваса – 50 рублей. Целью экономико-математической задачи является найти количество пива и кваса, которое должна производить фирма, чтобы прибыль от реализации была наибольшей.

При введении переменных нужно отталкиваться от вопроса задачи, поэтому за x1 и x2 примем соответственно количество пива и кваса, выпускаемое фирмой в сутки, выраженное в литрах, значит, по смыслу задачи x1 ≥ 0, x2 ≥ 0. Для изготовления напитков требуется определенное соотношение ресурсов, а также нужно учесть, что потребление ресурсов не может превышать их запасов, значит, определены первые условия системы ограничений: .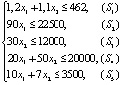

Здесь используются ресурсы: S1 – вода, S2 – солодовый концентрат, S3 – хлебный концентрат, S4 – сахар, S5 – дрожжи.

Далее нужно перевести оставшиеся дополнительные условия о суточной разнице спроса на напитки, об ограничениях в количестве 400 бутылок и в количестве пива 80 л, т.е. дописать условия x1 – 3×2 ≤ 0, x1 + x2 ≤ 400 и x1 ≤ 80. Эти неравенства соответствуют ресурсам: S6 – разница суточных спросов пива и кваса, S7 – количество используемых бутылок, S8 – спрос на пиво в сутки.

Целевая функция – это прибыль от реализации продаж, значит, F = 100×1 + 50×2 → max.

Задачи линейного программирования характеризуются некоторыми общими чертами. В каждой из них элементы решения представляют собой ряд неотрицательных переменных. Требуется также выбрать значения этих переменных, чтобы: выполнялись некоторые ограничения, имеющие вид линейных неравенств или неравенств относительно переменных; некоторая линейная функция F тех же переменных обращалась в максимум (минимум) [3, с. 11]. Полученная математическая модель производства относится к классу задач линейного программирования: найти F = 100×1 + 50×2 → max при системе ограничений .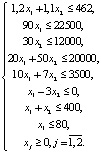

Используя алгоритм графического метода, необходимо:

1) построить область допустимых реше- ний;

2) отметить вектор 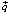, который проходит через точки (0;0) и (c1; c2), где c1 и c2 – коэффициенты при переменных в целевой функции. При определении максимума целевой функции направление вектора будет от точки (0;0) к точке (c1; c2), а при определении минимума – от точки (c1; c2) к точке (0;0);

3) изобразить линию уровня, проходящую через начало координат, т.е. прямую c1∙x1 + c2∙x2 = 0;

4) линию уровня переместить в направлении вектора 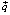. Перемещение линии уровня производится до тех пор, пока у нее не окажется только одна общая точка с областью допустимых решений. Эта точка определяет единственное решение задачи линейного программирования и будет точкой экстремума.

Границы области допустимых решений находятся из системы ограничений путем замены знаков неравенств равенствами, т.е.

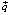
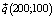
Вектор будет направлен от начала координат к точке (100; 50), однако в целях удобства масштаба рисунка можно удвоить координаты, получив в итоге .

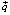
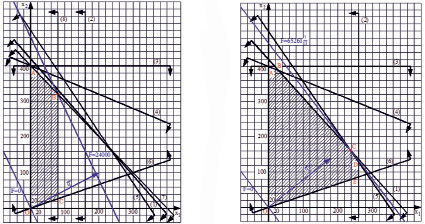
Линия уровня F = 0 или 100×1 + + 50×2 = 0 перемещается в направлении вектора до тех пор, пока линия уровня и область допустимых решений не будут иметь одну общую точку (на рис. 1(а) эта точка В). При этом значение целевой функции в этой точке равно Fmax = F(80, 320) = 24000.

Рис. 1. Нахождение оптимального решения графическим методом для начального условия (а) и измененного условия (б)

Подводя итог, можно отметить, что графическим способом был найден оптимальный план производства, а именно: если фирма будет производить за сутки 80 литровых бутылок пива и 320 литровых бутылок кваса, то можно получить наибольшую прибыль от продаж в размере 24 тыс. руб.

При решении многих экономических задач приходится рассматривать величины, принимающие только целые значения в силу своего экономического содержания. Подобные задачи относятся к задачам целочисленного линейного программирования [4].

Поскольку в результате решения задачи уже получилось решение x1 = 80, x2 = 320, то для целочисленного линейного программирования изменим условия. Запасы солодового концентрата равны 23 400 г, отсутствуют условия о том, что спрос на пиво не превышает 80 л за сутки и в день может использоваться не более 400 бутылок. Розничная цена за 1 л пива составит 180 рублей, за 1 л кваса – 140 рублей. Изменение условий задачи повлияет на составление математической модели. Теперь необходимо найти F = 180×1 + 140×2 → max при системе ограничений

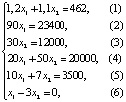
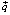
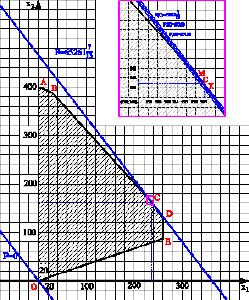
Границы области допустимых решений также изменяются в соответствии с новой системой, т.е. , а вектор будет направлен от начала координат к точке (180;140).

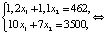
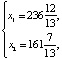
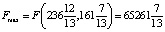
По рис. 1(б) точка оптимума – это точка С пересечения прямых (1) и (5); поскольку по графику видно, что она имеет нецелочисленные значения по осям координат, то найти координаты точки С можно, решив систему а целевая функция примет значение .

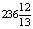
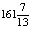
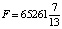
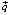
Как видно из решения, фирме необходимо выпустить литровых бутылок пива и бутылок кваса. Сделать это, конечно, не получится, поэтому требуется целочисленный ответ. Не всегда округление до целого значения в меньшую сторону обоих чисел дает наибольшую возможную прибыль, это зависит от соотношений сырья и его запасов, прибыли от продаж обоих напитков и иного, поэтому для нахождения целочисленного оптимума нужно увеличить часть рисунка возле точки С так, чтобы видна была каждая точка с целыми координатами в этой области. Линию уровня двигаем в направлении, обратном направлению вектора , до тех пор, пока не найдем первую целочисленную точку. Если есть сомнения в нескольких точках, можно их координаты подставить в целевую функцию и выбрать среди полученных значений наибольшее (рис. 2) [5].

Рис. 2. Нахождение оптимального решения графическим методом для целочисленного программирования

Определим значения целевой функции для точек X(237;161) и M(236;162), эти точки принадлежат области допустимых решений системы ограничений и являются ближайшими к точке оптимума С: F(X) = 180∙237 + 140∙161 = 65200; F(M) = 180∙236+140∙162 = 65160. Тогда Fmax цел = F(237, 161) = 65200.

Перейдем к анализу полученных решений. На рис. 1(а) и 1(б) можно увидеть, что не все прямые являются контурами границы области допустимых решений. Так, на рис. 1(а) область ограничена только прямыми (6), (7) и (8), а также осями координат, следовательно, условия системы ограничений, соответствующие прямым (1), (2), (3), (4) и (5), являются избыточными. На рис. 1(б) лишним является условие о ресурсе «хлебный концентрат», т.е. условие, соответствующее прямой (3). Все это говорит о том, что имелись неточности в определении ограничений.

На этом этапе нужно еще раз вернуться к началу и убрать лишние неравенства или скорректировать ограничения. Задача считается качественной, если каждое условие образует одну из сторон многоугольника решений. Если, например, сдвинуть некоторые прямые или изменить их наклон, то они уже будут давать новые стороны области решений. Таким образом, можно уменьшить либо количество неравенств в системе, либо запасы, пропорции и т.д.

Создадим итоговое условие задачи. Имеется фирма, которая выпускает 2 вида напитков: пиво и квас. Для изготовления пива используются 4 исходных продукта: вода, солодовый концентрат, сахар, дрожжи. Для изготовления кваса используются 4 исходных продукта: вода, хлебный концентрат, сахар, дрожжи. Расходы исходных продуктов на 1 л продукции и суточные запасы приведены в табл. 2.

Источник

Экономико-математические методы и модели и их классификация

Экономико-математическое моделирование служит для того, чтобы описывать системные социально-экономические процессы в виде экономико-математических моделей. Опираясь на определения метода моделирования и модели, можно сделать вывод, что экономико-математические методы – это своеобразный инструмент, а экономико-математические модели – это специфический продукт процесса экономико-математического моделирования.

Классификация экономико-математических методов

Говоря об экономико-математических методах, стоит отметить, что для них характерна своя классификация. Эти методы являются комплексом экономико-математических дисциплин, которые представляют собой сплав экономики, математики и кибернетики. В силу этих обстоятельств классификация экономико-математических методов сводится к классификации научных дисциплин, из которых она состоит. Однако стоит отметить, что общая классификация этих дисциплин не выработана окончательно до настоящего момента. Максимально приближённо можно выделить следующие разделы:

Экономическая кибернетика.
Математическая статистика.
Математическая экономика.
Методы принятия оптимальных решений.
Методы и дисциплины.
Методы экспериментального изучения экономических явлений.

Экономическая кибернетика

Экономическая кибернетика занимается системным анализом экономики, теории экономической информации и теорией управляющих систем.

Математическая статистика

Математическая статистика изучает экономические приложения данной дисциплины, которые представлены в виде выборочного метода, дисперсионного анализа, корреляционного анализа, регрессионного анализа, многомерного статистического анализа, факторного анализа, теории индексов и др.

Математическая экономика занимается исследованием вопросов, касающихся количественной стороны эконометрики. Здесь теория экономического роста, а также теория производственных функций и межотраслевые балансы. Кроме этого национальные счета, анализ спроса и предложения, региональный и пространственный анализ и др.

Методы принятия оптимальных решений

Методы принятия оптимальных решений в первую очередь касаются исследований и операций в экономике. Это самый объёмный раздел, который состоит из дисциплин и методов. Сюда входит оптимальное математическое программирование, сетевые методы планирования и управления, программно-целевые методы планирования и управления и многое другое. Одновременно с тем, оптимальное математическое программирование включает в себя линейное программирование, дискретно программирование, дробно-линейное программирование, стохастическое программирование, геометрическое программирование и др.

Методы и дисциплины

Методы и дисциплины здесь подразумеваются как для отдельной, так и для планируемой экономики с единым центром, а также для рыночной или, конкурентной. Первые – это теория наилучшей работы экономики, лучшее планирование, теория оптимального ценообразования, модели материально-технического снабжения и др. Вторые – методы, которые дают возможность разрабатывать модели незамещенной конкуренции, модели капиталистического цикла, модели монополии, модели индикаторного планированы, модели теории фирмы и др. Большинство из методов, которые были разработаны для централизованно планируемой экономики, могут эффективно применяться и при экономико-математическом моделировании в условиях рыночной экономики.

Методы экспериментального изучения экономических явлений

К данным методам можно отнести математические методы анализа и планирования экономических экспериментов, в том числе методы машинной имитации, а также деловые игры. Кроме того, к ним относятся методы экспертных оценок, которые могут быть применены для оценки явлений с непосредственным измерением.

Классификация экономико-математических моделей

Сразу стоит сказать, что единой системы классификации математических моделей социально-экономических систем и процессов не существует, но чаще всего говорят о десяти признаках их классификации. Вот некоторые из них.

Согласно общего целевого назначения всякие экономико-математические модели можно поделить на теоретико-аналитические, которые применяются для исследования общих свойств и закономерностей экономических процессов, и прикладные, применение которых происходит в условиях решения конкретных экономических задач анализа, прогнозирования и управления.

В соответствии со степенью агрегирования объектов моделирования модели делятся на макроэкономические и микроэкономические. Но важно понимать, что чёткого разграничения данные модели не имеют.

Также модели делятся по конкретному предназначению, иными словами, по своей цели создания и использования. Так выделяют балансовые модели, которые отражают все требования соответствия наличия ресурсов и их применения; трендовые модели, в которых развитие моделируемой экономической системы иллюстрируется посредством тренда её основных показателей; оптимизационные модели, которые предназначены для выбора наилучшего варианта их определённого числа вариантов производства, распределения или потребления; имитационные модели, которые призваны использоваться для машинной имитации изучаемых систем или процессов.

Также модели делятся по типу информации, которая используется в ней на аналитические, построенные на априорной информации и идентифицируемые, которые строятся на апостериорной информации.

Кроме этого все модели делятся на статистические, которые не зависят от момента времени, и динамические, описывающие экономические системы в развитии.

Ещё одним критерием является учётный фактор неопределённости модели, и они разделяются на детерминированные, если для них характерен на выходе однозначный результат управляющих воздействий, и стохастические, если на конечный результат могут оказывать влияние различные случайные факторы.

Кроме этого экономико-математические модели классифицируются по характеру математических объектов, входящих в состав или, что по сути одно и то же, по типу математического аппарата, который применён в данной модели. Этот признак помогает выделить следующие модели: матричные, модели линейного и нелинейного программирования, корреляционно-регрессионные модели, модели теории массового обслуживания, модели сетевого планирования и управления, и др.

И, наконец, различают модели по тому, к какому типу в изучении социально-экономических связей они относятся. Здесь можно говорить о дескриптивных и нормативных моделях. Дескриптивные модели образуют модели, которые предназначены для описания и объяснения фактически наблюдаемых явлений или для прогноза таких явлений. В качестве примера дескриптивной модели можно выбрать балансовую или трендовую модель.

Нормативные модели изучают совершенно иное. Их интерес заключается не в исследовании того, как устроена и развивается экономическая система, а в том, как она должна быть устроена и работать в соответствии с некоторыми критериями.

Все оптимизационные модели относятся к типу нормативных, в качестве примера можно использовать нормативные модели уровня жизни.

В качестве примера можно привести модель отраслевого баланса в разрезе экономико-математической модели. Если опираться на все классификации, которые были приведены выше, то можно сделать вывод, данная классификация является прикладной и макроэкономической. Ещё одна характеристика – аналитическая модель с дескриптивной функцией, которая является детерминированной, балансовой и матричной моделью. Важно отметить, что несмотря ни на что существуют статические, и динамические модели ЭММ МОБ.

Источник